文艺平衡树-splay的区间操作
真的是个神题,蒟蒻表示无力吐槽。刚开始以为是一个板子题,看着题解打了一遍,大概也理解了他是怎么实现的,然后我就去做别的题了,然后就在Three_D大佬的询问下蒙*了。最后还是问的nc哥,并思考了一个中午才搞明白。最主要的一点是,旋转不会改变树的中序遍历。
【建树操作】
对于一棵BST,区间[l,r],如果把l-1 splay到根,把r+1 splay到根的右子树,那么[l,r]即为根的右子树的左子树,如果不是BST,这个性质同样适用。然后因为旋转可能会涉及到1,n,所以要建立1,n+2两个哨兵节点;因为平衡树维护的是一个序列,所以一开始树的中序遍历应该是原序列:

1 rt=build_tree(0,1,n+2); 2 int build_tree(int fa,int l,int r) 3 { 4 if(l>r) return 0; 5 int mid=(l+r)>>1, 6 now=++sz; 7 key[now]=data[mid];f[now]=fa;tag[now]=0; 8 ch[now][0]=build_tree(now,l,mid-1); 9 ch[now][1]=build_tree(now,mid+1,r); 10 pushup(now); 11 return now; 12 }
【splay】
rotate不改变树的中序遍历,原rotate函数不变。因为要将r+2 splay到根的右节点而不是根,所以要多传一个参:

1 void splay(int x,int goal) 2 { 3 for(int fa;(fa=f[x])!=goal;rotate(x)) 4 if(f[fa]!=goal) 5 rotate(get(fa)==get(x)?fa:x); 6 if(!goal)rt=x; 7 }
【翻转区间】*
对于区间[l,r],将l splay到根,r+2 splay到根的右儿子,那么r+2的左子树就是[l+1,r+1].如果将r+2的左儿子的左右子树翻转,并递归地翻转下去,那么[l+1,r+1]的中序遍历就会翻转。但是这样的时间复杂度太高,所以延续线段树中懒标记的操作。

1 void turn(int l,int r) 2 { 3 l=rnk(l); 4 r=rnk(r+2); 5 splay(l,0); 6 splay(r,l); 7 pushdown(rt); 8 tag[ch[ch[rt][1]][0]]^=1; 9 }
然后说说把我弄懵逼的东西,对于序列 [12345],平衡树如图: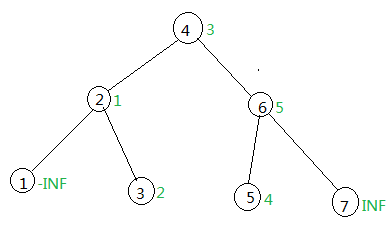
绿色的数字为key值,一定要注意区分节点的排名和这个节点的值,在建树时,key[now]=data[mid];当前节点的key存储的是序列的值,而图中黑色的数字是节点的排名,可能有点难以理解,那举个例子:
对于[12345],如果要翻转区间[2,3],那么在平衡树中找到排名为2的数(l=rnk(l)),即2,将他旋转到根,找到排名为5的数(r=rnk(r+2)),即5,将他旋转到根的右儿子,则5的左子树为[34],key值就是所要翻转的区间[23],打上标记,翻转完成。
Ps.除区间翻转外,还可以进行区间删除,区间加上x等操作。
【标记下传】
每到一个节点就要下传懒标记:

1 void pushdown(int x) 2 { 3 if(x && tag[x]) 4 { 5 tag[ch[x][0]]=tag[ch[x][0]]^1; 6 tag[ch[x][1]]=tag[ch[x][1]]^1; 7 swap(ch[x][0],ch[x][1]); 8 tag[x]=0; 9 } 10 }
【输出结果】
中序遍历整棵树即可:

1 void write(int now) 2 { 3 pushdown(now); 4 if(ch[now][0])write(ch[now][0]); 5 if(key[now]!=INF && key[now]!=-INF)cout<<key[now]<<" "; 6 if(ch[now][1]) write(ch[now][1]); 7 }
【完整代码】

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #define INF 0x7fffffff 5 using namespace std; 6 int n,m,data[1000000]; 7 int ch[1000000][2],size[1000000],cnt[1000000],f[1000000],key[1000000],tag[1000000],sz,rt; 8 9 int get(int x){return ch[f[x]][1]==x;} 10 void pushup(int x) 11 { 12 size[x]=size[ch[x][0]]+size[ch[x][1]]+1; 13 } 14 void pushdown(int x) 15 { 16 if(x && tag[x]) 17 { 18 tag[ch[x][0]]=tag[ch[x][0]]^1; 19 tag[ch[x][1]]=tag[ch[x][1]]^1; 20 swap(ch[x][0],ch[x][1]); 21 tag[x]=0; 22 } 23 } 24 int build_tree(int fa,int l,int r) 25 { 26 if(l>r) return 0; 27 int mid=(l+r)>>1, 28 now=++sz; 29 key[now]=data[mid];f[now]=fa;tag[now]=0; 30 ch[now][0]=build_tree(now,l,mid-1); 31 ch[now][1]=build_tree(now,mid+1,r); 32 pushup(now); 33 return now; 34 } 35 void rotate(int x) 36 { 37 int old=f[x],oldf=f[old],which=get(x); 38 pushdown(oldf),pushdown(old),pushdown(x); 39 ch[old][which]=ch[x][which^1];f[ch[old][which]]=old; 40 ch[x][which^1]=old;f[old]=x; 41 f[x]=oldf; 42 if(oldf) ch[oldf][ch[oldf][1]==old]=x; 43 pushup(old),pushup(x); 44 } 45 void splay(int x,int goal) 46 { 47 for(int fa;(fa=f[x])!=goal;rotate(x)) 48 if(f[fa]!=goal) 49 rotate(get(fa)==get(x)?fa:x); 50 if(!goal)rt=x; 51 } 52 int rnk(int x) 53 { 54 int now=rt; 55 while(1) 56 { 57 pushdown(now); 58 if(x<=size[ch[now][0]])now=ch[now][0]; 59 else 60 { 61 x-=size[ch[now][0]]+1; 62 if(!x)return now; 63 now=ch[now][1]; 64 } 65 } 66 } 67 void turn(int l,int r) 68 { 69 l=rnk(l); 70 r=rnk(r+2); 71 splay(l,0); 72 splay(r,l); 73 pushdown(rt); 74 tag[ch[ch[rt][1]][0]]^=1; 75 } 76 void write(int now) 77 { 78 pushdown(now); 79 if(ch[now][0])write(ch[now][0]); 80 if(key[now]!=INF && key[now]!=-INF)cout<<key[now]<<" "; 81 if(ch[now][1]) write(ch[now][1]); 82 } 83 signed main() 84 { 85 cin>>n>>m; 86 for(int i=1;i<=n;i++)data[i+1]=i; 87 data[1]=-INF,data[n+2]=INF; 88 rt=build_tree(0,1,n+2); 89 int x,y; 90 for(int i=1;i<=m;i++) 91 { 92 cin>>x>>y; 93 turn(x,y); 94 } 95 write(rt); 96 return 0; 97 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号 ヾ(≧O≦)〃嗷~
ヾ(≧O≦)〃嗷~