做题记录2
2020
3月
3月9日
UVA12467 Secret Word(KMP)
题意:给定一个字符串 \(s\) ,请找出一个 \(s\) 的最长子串,满足这个子串翻转后是 \(s\) 的前缀。
直接先把 \(s\) 翻转为 \(s'\) ,然后问题就是 \(s'\) 的子串在 \(s\) 的前缀能匹配的最长长度。
把 \(s\) 和 \(s`\) 拼接在一起,然后搞一个间隔符 '#' ,KMP 跑一遍,最长的匹配长度直接取 max 即可。
UVA12467 Secret Word(KMP)
没怎么看懂。。
CF1092C Prefixes and Suffixes(贪心)
CF1092C Prefixes and Suffixes(贪心)
贪心地想,如果我们排一下序,那么大的必须包含小的。
所以我们先预处理出每个串可作为前缀还是后缀(亦或两者皆可),然后:
对于每种拼接方法——
如果一个串可以放在前缀的位置而不能放在后缀的位置,就把b[i]设为1。
如果一个串可以放在后缀的位置而不能放在前缀的位置,就把b[i]设为2。
如果一个串可以放在前缀的位置也可以放在后缀的位置,就把b[i]设为0。
如果都不能放,就说明这种情况不可行。
然后对于两个b为0的相同子串,用一个map存储,分别放在前缀和后缀就好了。
判断的话直接暴力即可。
类似的处理办法也可以。
CF314B Sereja and Periods(贪心)
首先,我们可以把 \([c,d]\) 直接先拆掉,让 \(a\) 和 \(c\) 先匹配,最后 \(/d\) 即可。
于是我们考虑 \(a\) 和 \(c\) 的匹配。
我们直接枚举 \(a\) 的每一个点去匹配 \(c\) ,然后记录一下匹配了多少个 \(c\) ,以及匹配完过后到了哪个位置。
所以这里相当于我们有 \(b\) 个 \(a\) 用于匹配(相当于现在我们有 \(b\) 个 \(a\) 可以拿来用),所以直接对于每一轮的 \(a\) ,先加上这次匹配了多少个 \(c\) ,再跳转到之前预处理出来的跳转完过后的位置。
具体见代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)) f|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=f?-x:x;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
}
#define ll long long
const int N=205;
ll cnt[N];
char s[N],p[N];
int b,d,n,m,Turn[N];
int main(){
read(b),read(d);
scanf("%s",s),scanf("%s",p);
n=strlen(s),m=strlen(p);
for(int i=0;i<m;i++){
int now=i;
for(int j=0;j<n;j++)if(s[j]==p[now]){now++;if(now==m) now=0,cnt[i]++;} //暴力预处理匹配
Turn[i]=now;
}
ll ans=0;int now=0;
for(int i=1;i<=b;i++) ans+=cnt[now],now=Turn[now];//跳转
write(ans/d);
return 0;
}
CF808G Anthem of Berland(KMP+DP)
CF808G Anthem of Berland(KMP+DP)
首先想到 dp 。
然后显然我们要转移的 \(dp[i]\) 从 \(dp[i-len]\) 而来,但是有问题。
就是可能我们会重复利用某一段区间内的字符,比如 ababa ,然后要匹配的是 aba 。
显然中间的那个 a 被两个串都用到了,而我们不能像之前那样转移。
所以我们考虑把中间重复的也计算出来。
发现出现重复,即代表一段相等的前后缀。
于是想到 KMP 来跳转,但是这样还不够,另外还有一个 \(g\) 数组,具体见题解。

P4051 [JSOI2007]字符加密(SA)
寻找最小的循环移动位置
SA 板子题。
直接把原串复制一遍然后拼接,跑一遍 SA 就相当于直接排序了。
然后容易发现多出来的一些后缀是无用的,因为我们总能在这些后缀的前几个里面就比较出大小。
贴一下代码:
scanf("%s",str+1);
k=strlen(str+1);n=k<<1;
for(int i=1;i<=k;i++) str[i+k]=str[i];
SA();
for(int i=1;i<=n;i++) if(sa[i]<=k) putchar(str[sa[i]+k-1]);
SP705&SP694 SUBST1 - New Distinct Substrings(SA)
SP705&SP694 SUBST1 - New Distinct Substrings(SA)
不同子串的数目
有个结论:

然后直接模拟即可,注意清零。
P2743 [USACO5.1]乐曲主题Musical Themes(SA+二分)
P2743 [USACO5.1]乐曲主题Musical Themes(SA+二分)
可重叠最长重复子串
不是这道题,怎么做就是询问 Height 数组的最大值即可。
不可重叠最长重复子串
先差分一下,然后跑 SA 。
我们二分最长的重复出现长度 \(k\) 。
那么现在任务是判断,我们直接遍历 1~n ,如果相邻两个的 \(LCP(i,i-1) \geq k\) ,则我们可以计算一下这个 \(LCP\geq k\) 的“块”的最大位置和最小位置,最后我们直接判断两个相减有没有两个 \(k\) 长即可。
放一下代码:
int ans,T;
char c[N];
bool Check(int k){
int Max,Min;
for(int i=1;i<=n;i++){
if(he[i]<k) Max=Min=sa[i];
else{
Max=max(Max,sa[i]);
Min=min(Min,sa[i]);
if(Max-Min>k) return true;
}
}
return false;
}
int main(){
read(n);
for(int i=1;i<=n;i++) read(str[i]);
for(int i=1;i<=n;i++) str[i]=str[i+1]-str[i]+100;
SA();
int l=1,r=n/2+1;
while(l<=r){
int mid=l+r>>1;
if(Check(mid)) l=mid+1,ans=mid;
else r=mid-1;
}
write(ans>=4?ans+1:0);
return 0;
}
SP687 REPEATS - Repeats(SA+ST表+分块)
SP687 REPEATS - Repeats(SA+ST表+分块)
简要题意:给定字符串,求重复次数最多的连续重复子串。
连续的若干个相同子串
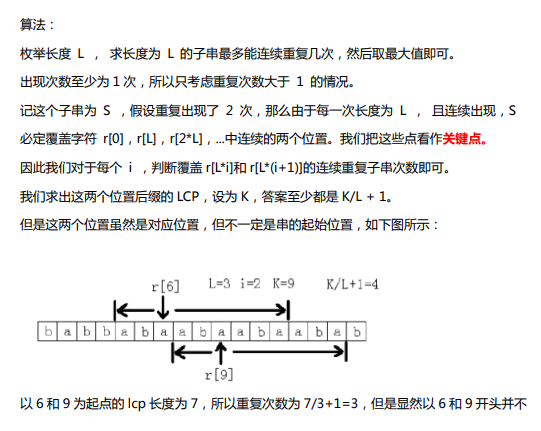

CF438D The Child and Sequence(势能线段树)
CF438D The Child and Sequence(势能线段树)
题意:给定数列,区间查询和,区间取模,单点修改。
势能线段树。
因为区间取模每次至少减少一个数的一半,所以一个数最多减少 \(logn\) 次,总复杂度是 \(nlogn\) 。
于是代码:
int Max[N<<2],Sum[N<<2],a[N];
void Pushup(int x){
Max[x]=max(Max[x<<1],Max[x<<1|1]);
Sum[x]=Sum[x<<1]+Sum[x<<1|1];
return ;
}
void Build(int x,int l,int r){
if(l==r){
Max[x]=Sum[x]=a[l];
return ;
}
int mid=l+r>>1;
Build(x<<1,l,mid);
Build(x<<1|1,mid+1,r);
Pushup(x);
return ;
}
void Modify(int x,int l,int r,int ql,int qr,int p){
if(Max[x]<p) return ;
if(l==r){
Max[x]%=p,Sum[x]%=p;
return ;
}
int mid=l+r>>1;
if(ql<=mid) Modify(x<<1,l,mid,ql,qr,p);
if(qr>mid) Modify(x<<1|1,mid+1,r,ql,qr,p);
Pushup(x);
return ;
}
void Change(int x,int l,int r,int pos,int v){
if(l==r){Max[x]=Sum[x]=v;return ;}
int mid=l+r>>1;
if(pos<=mid) Change(x<<1,l,mid,pos,v);
else Change(x<<1|1,mid+1,r,pos,v);
Pushup(x);
return ;
}
int Query(int x,int l,int r,int ql,int qr){
if(ql<=l&&r<=qr) return Sum[x];
int mid=l+r>>1;int res=0;
if(ql<=mid) res+=Query(x<<1,l,mid,ql,qr);
if(qr>mid) res+=Query(x<<1|1,mid+1,r,ql,qr);
return res;
}
CF920F SUM and REPLACE(势能线段树)
区间把一个数变为其因数个数。
同样是势能线段树,每次至少减少一半。
减到小于等于2的时候直接不用管。
还有个关键是线性筛每个数的因数个数(这是个积性函数)。
具体见这里。
代码:
bool vis[N];
int prime[N],t[N],e[N];
void PreWork(int K){
int cnt=0;t[1]=1;
for(int i=2;i<=K;i++){
if(!vis[i]) prime[++cnt]=i,t[i]=2,e[i]=1;
for(int j=1;j<=cnt;j++){
if(i*prime[j]>K) break;
vis[i*prime[j]]=true;
if(i%prime[j]==0){t[i*prime[j]]=t[i]/(e[i]+1)*(e[i]+2);e[i*prime[j]]=e[i]+1;break;}
else t[i*prime[j]]=t[i]*2,e[i*prime[j]]=1;
}
}
return ;
}
int Max[N<<2],Sum[N<<2],a[N];
void Pushup(int x){
Max[x]=max(Max[x<<1],Max[x<<1|1]);
Sum[x]=Sum[x<<1]+Sum[x<<1|1];
return ;
}
void Build(int x,int l,int r){
if(l==r){
Max[x]=Sum[x]=a[l];
return ;
}
int mid=l+r>>1;
Build(x<<1,l,mid);
Build(x<<1|1,mid+1,r);
Pushup(x);
return ;
}
void Modify(int x,int l,int r,int ql,int qr){
if(Max[x]<=2) return ;
if(l==r){
int k=t[Max[x]];
Max[x]=Sum[x]=k;
return ;
}
int mid=l+r>>1;
if(ql<=mid) Modify(x<<1,l,mid,ql,qr);
if(qr>mid) Modify(x<<1|1,mid+1,r,ql,qr);
Pushup(x);
return ;
}
int Query(int x,int l,int r,int ql,int qr){
if(ql<=l&&r<=qr) return Sum[x];
int mid=l+r>>1;int res=0;
if(ql<=mid) res+=Query(x<<1,l,mid,ql,qr);
if(qr>mid) res+=Query(x<<1|1,mid+1,r,ql,qr);
return res;
}
3月10日
5784【Day9-1】市场(势能线段树)
题意:

区间加和区间除。
其实势能线段树的关键就是对于一些区间的合并。
而区间除不好维护,所以我们选择区间减法。

然后考虑时间复杂度:

重点代码:
void add(int o,int l,int r,int L,int R,int dla){
if (L<=l&&r<=R) {
sum[o]+=(r-l+1)*dla; mx[o]+=dla; mn[o]+=dla;
lazy[o]+=dla; return;
}
if (lazy[o]&&l!=r) down(o,l,r);
if (L<=Mid) add(ls,L,R,dla);
if (R> Mid) add(rs,L,R,dla);
up(o);
}
void upt(int o,int l,int r,int L,int R,int dla){
if (L<=l&&r<=R&&chu(mx[o],dla)-mx[o]==chu(mn[o],dla)-mn[o]) {
add(o,l,r,L,R,chu(mx[o],dla)-mx[o]); return;
}
if (lazy[o]&&l!=r) down(o,l,r);
if (L<=Mid) upt(ls,L,R,dla);
if (R> Mid) upt(rs,L,R,dla);
up(o);
}
#228. 基础数据结构练习题(势能线段树)

同样转化成区间减法。
当区间最大值和最小值之差小于等于 1 的时候,直接打标记。
不然暴力递归到单点暴力修改。
势能线段树总结

小朋友的笑话(势能线段树)
最关键的一点是如何处理某个笑话在某个点是否重复出现过。
单独考虑某一个笑话,问题就转化为区间覆盖,求哪些位置是第一次被覆盖。考虑用 set 维护所有区间,第一关键字为左端点。对于当前要插入的区间 [l,r] ,我们可以利用 lower_bound 很方便的求出所有与这个区间有交集的区间。我们先把 [l,r] 都标记为在笑,然后依次扫描刚才找到的有交集的区间,把交集部分标记为没在笑。最后再向 set 中插入这个区间。这样的修改和查询都可以用线段树解决。
但是这样的时间复杂度不能保证。所以,每次我们都要把上面扫描到的区间以及当前区间都合并成一个区间。这样,每个区间都只会插入、修改、合并一次。这样就可以通过了。
P4891 序列(势能线段树+线段树上二分)
核心:
\(1.\) 势能线段树:如果一段区间内都满足 \(c_i\geq b_i\) ,那么这段区间可以合为一段,这时我们要给 \(c_i\) 的一段区间加就是直接打标记就可以了。
\(2.\) 线段树上二分:因为题意其实是对 \(a\) 数组单点修改,而这里反应到 \(c\) 数组上面就是
剩下的细节看 CQA 的题解来秀吧。(其实就是我写挂了直接 T 飞了/kk。)

Buy Tickets(线段树上二分)
题目大意:插队的问题,每个案例给出 \(n\),代表有 \(n\) 个插队的,每个给出 \(p\),\(v\) 意思是代号为 \(v\) 的人插在了第 \(p\) 个人的后面,问最后的队伍的排列?
倒序插入,每次插入根据空格数量插入。
比如如果我们插入当前的第 \(p\) 个人后面,我们就在线段树上看当前左子树够不够 \(p+1\) 个空位,然后选择 去/不去 即可。
P4198 楼房重建(线段树上二分)
详见这里
Mex(线段树上二分)
题意:求所有区间的 mex 和,mex 值为没有在该区间出现过的最小非负整数。
想法是每次求以i为起点的区间的mex值的和,最后累加即为答案。
可以先预处理出1为起点的区间的mex值,用它构造一棵线段树,要有求和和求最大值的操作。
构造好线段树之后,1为起点的区间的mex和已经得到了,就是sum[1]。
接下来求2为起点的,首先第一步要删掉a[1],这里把mex[1]置为0。
删掉val=a[1]这个元素对后面的有什么影响呢?易知它不会对下一个出现val(下一个出现val的位置是nex[1])之后的位置产生影响,因为后面的区间已经包含val了(不少它这一个)。
然后我们需要求得大于val的最大mex的位置pos,线段树单点查询最大值即可得到。
对于pos到nex[1] - 1的元素,所有的mex值都要变成a[i](不难想),成段更新线段树即可。
这样就得到了2为起点的区间的mex和,sum[1]。
代码:
void pushup(int rt){
sum[rt]=sum[rt<<1]+sum[rt<<1|1];
maxmex[rt]=max(maxmex[rt<<1],maxmex[rt<<1|1]);
}
void build(int l,int r,int rt){
_set[rt]=0;
if(l==r){
sum[rt]=maxmex[rt]=mex[l];
return ;
}
int m=(l+r)>>1;
build(lson);
build(rson);
pushup(rt);
}
void pushdown(int rt,int len){
if(_set[rt]){
_set[rt<<1]=_set[rt<<1|1]=1;
sum[rt<<1]=maxmex[rt]*1ll*(len-(len>>1));
sum[rt<<1|1]=maxmex[rt]*1ll*(len>>1);
maxmex[rt<<1]=maxmex[rt<<1|1]=maxmex[rt];
_set[rt]=0;
}
}
void update(int L,int R,int v,int l,int r,int rt){
if(L<=l&&r<=R){
_set[rt]=1;
sum[rt]=1ll*(r-l+1)*v;
maxmex[rt]=v;
return ;
}
pushdown(rt,r-l+1);
int m=(l+r)>>1;
if(L<=m) update(L,R,v,lson);
if(R>m) update(L,R,v,rson);
pushup(rt);
}
int query(int x,int l,int r,int rt){
if(l==r){
return l;
}
pushdown(rt,r-l+1);
int m=(l+r)>>1;
int ans;
if(x<maxmex[rt<<1]) ans=query(x,lson);
else ans=query(x,rson);
return ans;
}
CF817F MEX Queries(线段树上二分)
先离散化,然后题目就是区间赋值 0/1 和区间取反。
询问就是对于当前点检查左子树是否和不等于区间长度,是则递归左边,不然递归右边,递归到最后单点直接返回单点位置。
代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=5e5+5;
#define int long long
int n,m;
struct Query{int op,l,r;}Q[N];
int b[N],cnt;
int Sum[N<<2],tag[N<<2];
void Pushup(int x){
Sum[x]=Sum[x<<1]+Sum[x<<1|1];
return ;
}
void PushDown(int x,int l,int r){
if(!tag[x]) return ;
int mid=l+r>>1;
if(tag[x]==3){
if(tag[x<<1]!=3) tag[x<<1]^=3;
else tag[x<<1]=0;
if(tag[x<<1|1]!=3) tag[x<<1|1]^=3;
else tag[x<<1|1]=0;
Sum[x<<1]=mid-l+1-Sum[x<<1];
Sum[x<<1|1]=r-mid-Sum[x<<1|1];
}
else tag[x<<1]=tag[x<<1|1]=tag[x],Sum[x<<1]=(tag[x]&1)*(mid-l+1),Sum[x<<1|1]=(tag[x]&1)*(r-mid);
tag[x]=0;
return ;
}
void Modify(int x,int l,int r,int ql,int qr,int v){
if(ql<=l&&r<=qr){
if(v==1) Sum[x]=r-l+1,tag[x]=1;
else if(v==2) Sum[x]=0,tag[x]=2;
else{
Sum[x]=r-l+1-Sum[x],tag[x]^=3;
}
return ;
}
PushDown(x,l,r);
int mid=l+r>>1;
if(ql<=mid) Modify(x<<1,l,mid,ql,qr,v);
if(qr>mid) Modify(x<<1|1,mid+1,r,ql,qr,v);
Pushup(x);
return ;
}
int Query(int x,int l,int r){
if(l==r){
if(!Sum[x]) return l;
else return -1;
}
PushDown(x,l,r);
int mid=l+r>>1,Ans;
if(Sum[x<<1]<mid-l+1) Ans=Query(x<<1,l,mid);
else Ans=Query(x<<1|1,mid+1,r);
Pushup(x);
return Ans;
}
signed main(){
read(n);
for(int i=1;i<=n;i++){
read(Q[i].op),read(Q[i].l),read(Q[i].r);
b[++cnt]=Q[i].l,b[++cnt]=Q[i].r,b[++cnt]=Q[i].r+1;
}
b[++cnt]=1;
sort(b+1,b+cnt+1);
int idx=unique(b+1,b+cnt+1)-b-1;
for(int i=1;i<=n;i++){
Q[i].l=lower_bound(b+1,b+idx+1,Q[i].l)-b,Q[i].r=lower_bound(b+1,b+idx+1,Q[i].r)-b;
Modify(1,1,idx,Q[i].l,Q[i].r,Q[i].op);
int x=Query(1,1,idx);
write(b[x]),putchar('\n');
}
return 0;
}
CF609F Frogs and mosquitoes(线段树+set)
CF609F Frogs and mosquitoes(线段树+set)
发现大区间覆盖小区间时可以合并,区间有交时也可以分。
于是可以用线段树维护当前覆盖情况,然后用 set 维护合并和虫子。
代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=2e5+5;
#define ll long long
int n,m,w[N],t[N],c[N],d[N],a[N*4];
multiset<pair<int,int> > st;
bool cmp(int u,int v){return w[u]<w[v];}
int Modify(int p,int v,int x,int l,int r){
if(p<l||p>=r) return a[x];
if(l+1==r) return a[x]=w[d[p]]+v;
int mid=(l+r)>>1;
return a[x]=max(Modify(p,v,x<<1,l,mid),Modify(p,v,x<<1|1,mid,r));
}
int Query(int p,int x,int l,int r){
if(l+1==r)return (a[x]>=p&&w[d[l]]<=p)?l:-1;
int mid=(l+r)>>1;
return a[x<<1]>=p?Query(p,x<<1,l,mid):Query(p,x<<1|1,mid,r);
}
int main(){
read(n),read(m);
for(int i=0;i<n;i++) read(w[i]),read(t[i]),d[i]=i;
sort(d,d+n,cmp);
for(int i=0;i<n;i++) Modify(i,t[d[i]],1,0,n);
while(m--){
int p,b;read(p),read(b);
int i,k=Query(p,1,0,n);
if(k==-1)st.insert({p,b});
else{
i=d[k],c[i]++,t[i]+=b;
while(st.size()){
multiset<pair<int,int> >::iterator it=st.lower_bound({w[i],-1});
if(it==st.end()||w[i]+t[i]<it->first)break;
c[i]++,t[i]+=it->second,st.erase(it);
}
Modify(k,t[i],1,0,n);
}
}
for(int i=0;i<n;i++) write(c[i]),putchar(' '),write(t[i]),putchar('\n');
return 0;
}
3月11日
CF19D Points(线段树上二分+set)
首先看到值域的数据范围我们可以想到先离散化一下。
然后我们考虑用线段树维护横坐标为 \(1,2,3,4...\) 时的纵坐标最大值。(也就是每一个横坐标上的最大纵坐标,在这个基础上线段树维护最大值。)
对于每一个横坐标可以开一个 set 维护这个坐标内部的点。
那么题目上的操作就很好实现了,添加操作就是先看看可不可以取代当前的那个位置上的最大值,然后再插入进 set 里。
删除操作就是先在对应横坐标的 set 里删除,然后再用当前 set 里的最大值放进线段树里,覆盖掉原来的那个。
最后 查找操作就是先在线段树上二分,找到最左边的,且横坐标大于 \(x\) ,值大于 \(y\) 的位置。
(注意这里的值指的是线段树维护的那个 \(Max\) ,因为我们这里只是看在这个坐标上有没有解,至于题目要求的还要 \(y\) 尽可能小,我们一会先定位横坐标,再在这个横坐标的 set 上找。)
于是我们再在这个位置上的 set 当中二分找到第一个大于 \(y\) 的值,再映射回原数组(因为离散化了的),就是答案了。
代码如下:
const int N=4e5+5;
#define ll long long
struct Query{int op,x,y;}Q[N];
int n,m,b[N],cnt,Max[N<<2];
set<int> ST[N];
void Pushup(int x){Max[x]=max(Max[x<<1],Max[x<<1|1]);return ;}
void Modify(int x,int l,int r,int pos,int v){
if(l==r){Max[x]=max(Max[x],v);return ;}
int mid=l+r>>1;
if(pos<=mid) Modify(x<<1,l,mid,pos,v);
else Modify(x<<1|1,mid+1,r,pos,v);
Pushup(x);
return ;
}
void Change(int x,int l,int r,int pos,int v){
if(l==r){Max[x]=v;return ;}
int mid=l+r>>1;
if(pos<=mid) Change(x<<1,l,mid,pos,v);
else Change(x<<1|1,mid+1,r,pos,v);
Pushup(x);
return ;
}
int QueryPos(int x,int l,int r,int X,int Y){
if(l==r){
if(Max[x]>Y) return l;
return -1;
}
int mid=l+r>>1,res=-1;
if(X<=mid&&Max[x<<1]>Y) res=QueryPos(x<<1,l,mid,X,Y);
if(~res) return res;
if(Max[x<<1|1]>Y) return QueryPos(x<<1|1,mid+1,r,X,Y);
return -1;
}
int main(){
read(n);
for(int i=1;i<=n;i++){
char op[10];int x,y;
scanf("%s",op);read(x),read(y);
if(op[0]=='a') Q[i].op=1,Q[i].x=x,Q[i].y=y;
else if(op[0]=='r') Q[i].op=2,Q[i].x=x,Q[i].y=y;
else Q[i].op=3,Q[i].x=x,Q[i].y=y;
b[++cnt]=x,b[++cnt]=y;
}
sort(b+1,b+cnt+1);
int idx=unique(b+1,b+cnt+1)-b-1;
for(int i=1;i<=n;i++) Q[i].x=lower_bound(b+1,b+idx+1,Q[i].x)-b,Q[i].y=lower_bound(b+1,b+idx+1,Q[i].y)-b;
for(int i=1;i<=n;i++){
if(Q[i].op==1) ST[Q[i].x].insert(Q[i].y),Modify(1,1,idx,Q[i].x,Q[i].y);
else if(Q[i].op==2) ST[Q[i].x].erase(*ST[Q[i].x].end()),Change(1,1,idx,Q[i].x,*ST[Q[i].x].end());
else{
int Pos=QueryPos(1,1,idx,Q[i].x+1,Q[i].y);
if(Pos==-1) puts("-1");
else write(b[Pos]),putchar(' '),write(b[*ST[Pos].upper_bound(Q[i].y)]),putchar('\n');
}
}
return 0;
}
P5579 [PA2015]Siano(线段树上二分+标记)
P5579 [PA2015]Siano(线段树上二分+标记)
思路和题解一样:

这个题的主要 Trick 就是发现在割草过后速率高草的永远比速率低草的要高。
于是我们每一次操作可以通过:按这个生长速率排一下序使其满足速率单调上升。
然后就实现了每一次的割草都变成了连续的一段区间操作。
于是我们这道题的线段树上二分就是:找到最左边的,其高度大于等于当前要割的高度的点。
然后注意一下标记即可。
HDU5930 GCD(线段树上二分)
3月12日
CF1495A Diamond Miner(贪心+排序)
一眼题。
主要是一个 Trick ,把大的数和大的数放到一起,小的和小的放到一起。
直接 sort 过后对应匹配统计答案就行了。
CF1495B Let's Go Hiking(博弈+DP)
CF1495B Let's Go Hiking(博弈+DP)
第一步,我们分析得出每个人不能走回头路,证明显然。
首先,我们发现一个人可以走的更远,当且仅当这是一个连续单调 上升/下降 的序列。
那么其实在我们选定最初 \(x\) 的位置时,他能走的路线就已经确定了,也就是只能朝着单调下降的一段不停地往前走,直到单调区间的尽头。
而这个时候 \(y\) 的应对也很容易。
首先我们发现,既然答案跟单调区间长度有关,那么我们就直接求出最长的单调 上升/下降 区间即可。
顺便记一下最大值的个数,因为如果有超过 2 个这样的区间,那么对于 \(x\) 而言是必败。
(至于为什么是 2 个不是 1 个:因为如果超过 1 个,但是两个区间首尾相接并且正好相反,也就是呈现 '^' 形状,这个需要单独讨论,x 并不是必败。)
为什么呢?因为 \(x\) 无论选择哪个最长单调区间,\(y\) 都可以选择另外一个区间,其长度和 \(x\) 的长度一样,并且这样的话 \(x\) 接下来只能走 \(len-1\) 步,而 \(y\) 相对于 \(x\) 要多一步。(因为 \(x\) 先手)
那么现在再讨论刚好有一个的情况:
这样的情况其实很简单,\(x\) 随便选哪个点, \(y\) 直接选 \(x\) 下端的那一个点,此时该 \(x\) 走,但他被 \(y\) 挡住了,直接就输了。
最后是刚好两个这样的区间,且首尾相接,且呈现 '^' 状的情况。
\(x\) 此时选择 '^' 的顶点, \(y\) 堵哪一边都不行,因为 \(x\) 直接反方向走即可,但是我们考虑 \(x\) 反方向走行吗?
比如此时我的 \(y\) 放在左下角,\(x\) 如果走另一边,显然这是和之前那个 “两个以上区间” 的情况一样,\(x\) 因为先手会死掉。
(但是,这也是 \(y\) 最大的限制,那就是此时 \(y\) 只能放在两端的末尾,不能放在山坡上的任何中间一个位置,因为这样的话 \(x\) 走另一边就比 \(y\) 长了。)
那么此时 \(x\) 只能走 \(y\) 的同侧,且 \(y\) 只能放在一段末尾,那在这个时候,\(x,y\) 的行动轨迹完全确定了,我们只需要考虑最后模拟出来的胜者是谁即可。
模拟几下会知道:\(x\) 会胜当且仅当这个山坡长度是奇数时。(此时 \(x\) 在最后会走到中点 mid ,而 \(y\) 会走到 mid-1 ,此时该 \(y\) 走,但是他被 \(x\) 挡住了,\(y\) 动不了了,所以 \(x\) 胜。)
代码如下:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=1e5+5;
int T,n,m,tot;
int a[N],dp[N],Maxn,Maxn1,Max,dp1[N];
int main(){
T=1;
while(T--){
read(n);tot=Max=Maxn=Maxn1=0;
for(int i=1;i<=n;i++){
read(a[i]);
if(a[i]>a[i-1]) dp[i]=dp[i-1]+1;
else dp[i]=1;
if(a[i]<a[i-1]) dp1[i]=dp1[i-1]+1;
else dp1[i]=1;
Maxn=max(Maxn,dp[i]);
Maxn1=max(Maxn1,dp1[i]);
}
Max=max(Maxn,Maxn1);
bool flag=false,flag1=false;
int pos1,pos;
for(int i=1;i<=n;i++){
if(dp[i]==Max) tot++,flag=true,pos=i;
if(dp1[i]==Max) tot++,flag1=true,pos1=i;
}
if(tot==2&&flag&&flag1&&pos==pos1-Max+1&&(Max&1)) puts("1");
else puts("0");
}
return 0;
}
CF1495C Garden of the Sun(构造)
假设初始是这样的:(借用官方图)

我们可以这样构造:
在列 \(2,5,8,11...\) 处直接填满,这样是不会出现环的,因为题目说了保证每一个初始的空地没有公共点和公共边。
然后就变成了这样:

现在的任务就是把这样类似的三列一块,三列一块的连通块连接起来:

怎么做呢?就是把之前 \((3,4),(6,7),(9,10)...\) 这中间的几列本来就有的点延伸过去(如果这两列都没有的话就直接强行填两个连着的不就好了吗。)
这样就能保证联通了,但是我们还要考虑最后两行的状态:(注意这样的情况只有在 n%3=2 的时候才会出现。)
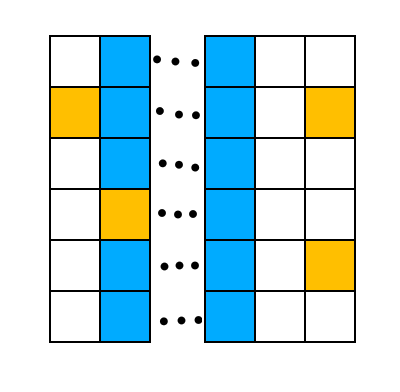
在倒数第二列的,我们根本不用连,而在倒数第一列的,我们直接把其左边的那个变成空地就行了。

我们这样就得到了一个 \(O(n^2)\) 的算法,可以通过。
代码如下:
const int N=505;
int T,n,m;
char W[N][N];
int main() {
read(T);
while(T--){
read(n),read(m);
for(int i=1;i<=n;i++) scanf("%s",W[i]+1);
for(int i=1;i<=n;i+=3)for(int j=1;j<=m;j++) W[i][j]='X';
for(int i=3;i<n;i+=3){
int flag=0;
for(int j=1;j<=m;j++) if(W[i][j]=='X') {W[i-1][j]='X';flag=1;break;}
if(!flag) for(int j=1;j<=m;j++) if(W[i-1][j]=='X') {W[i][j]='X';flag=1;break;}
if(!flag) W[i-1][1]=W[i][1]='X';
}
if(n%3==0) for(int i=1;i<=m;i++) if(W[n][i]=='X')W[n-1][i]='X';
for(int i=1;i<=n;i++) printf("%s\n",W[i]+1);
}
return 0;
}
P7323 [WC2021] 括号路径(启发式合并+并查集)
P7323 [WC2021] 括号路径(启发式合并+并查集)
考场傻逼就是我。
我们可以发现几个性质:
\(1.\) 对于两个点如果可以互相到达,那么我们可以把他们视作一个点。
\(2.\) 对于两个点可以互相到达,当且仅当他们有同类边指向同一个点。
正确性显然。
于是我们考虑把原图缩成一个个连通块,最后答案就是 \(\sum{Siz_x \times (Siz_x-1)/2}\)。
那么现在在于怎么维护连通块。
我们使用并查集。
对于每两个点,如果可以合并,那么就把其中一个点的所有可以和它合并的点也都合并过去(就是把合并关系记下来,一个一个去合并。)。
于是在这个过程中我们直接并查集启发式合并即可,反正也要用 \(Siz\) 。
代码如下:
int n,m,k;
int siz[N],fa[N];
int Find(int x){return x==fa[x]?x:fa[x]=Find(fa[x]);}
map<int,int> Map[N];
queue<PII> q;
void Merge(int x,int y){
x=Find(x),y=Find(y);
if(x==y) return ;
if(siz[x]<siz[y]) swap(x,y);
for(map<int,int>::iterator it=Map[y].begin();it!=Map[y].end();it++){
int col=it->first,z=it->second;
if(Map[x][col]) q.push(make_pair(Map[x][col],z));
else Map[x][col]=z;
}
siz[x]+=siz[y];
fa[y]=x;
return ;
}
int main(){
read(n),read(m),read(k);
for(int i=1;i<=n;i++) fa[i]=i,siz[i]=1;
for(int i=1,u,v,w;i<=m;i++){
read(u),read(v),read(w);
if(Map[v][w]) q.push(make_pair(Map[v][w],u));
else Map[v][w]=u;
}
while(!q.empty()){
PII p=q.front();q.pop();
int u,v;
u=p.first,v=p.second;
Merge(u,v);
}
ll ans=0;
for(int i=1;i<=n;i++) if(fa[i]==i) ans+=1ll*siz[i]*(siz[i]-1)/2;
write(ans);
return 0;
}
P7325 [WC2021] 斐波那契(数论,Exgcd,逆元,性质)
P7325 [WC2021] 斐波那契(数论,Exgcd,逆元,性质)
容易把原题目转化成求 $a\times F_{i-1} + b \times F_i \equiv 0 $ \((\) \(mod\) \(m\) \()\) 中的 \(n\) 。
然后做法就是把原式化为最小等价形式,然后对于所有可能的等价形式我们都直接先预处理,最后直接转化一下再找答案输出即可。
暂不赘述,详见这篇题解。
CF1494E A-Z Graph(性质)
给一个 \(n\) 个点的图,每次可以加一条边或者删一条边,边权是一个 a-z 的字符,保证没有重边自环,每次询问图上存不存在长度为 \(k\) 的路径使得该路径上的边权构成的字符串是个回文串。
手玩一下样例就能知道如果存在环,那么回文的条件必然可以达成。
那么又因为我们题目的基础,有这样的事实:一个大环,必定路径上的每两个点都有小环(也就是一去一回,不然大环也构不成)。
那么我们观察一下小环,发现一个非常好的性质:我们可以在小环上反复横跳,这样得出的字符串一定回文。
但是有一个问题,就是这样的话得出的字符串全是偶数。
所以对于奇数,相当于我们必须得要这一去一回的两条边完全相同才行。
那么我们问题就转换成了计数,每次看图中的二元环个数和二元环且两边相等的个数是不是大于 0 即可。
这个我们直接用 map 维护一下就好了。
CF1494D Dogeforces(贪心,递归)
我们容易发现每个点和其他点必定有一个点的 LCA 是当前树的根,那么这个根的值一定是最大值。
所以每次我们可以确定一个树的根,再递归下去处理即可。
CF1486F Pairs of Paths(LCA+结论+树状数组+DFS序+差分)
CF1486F Pairs of Paths(LCA+结论+树状数组+DFS序+差分)
最重要的 Trick :指定一个根,则两条路径的交一定过一条路径的 LCA。
然后就是枚举深度更深的那个 LCA 过后讨论情况统计答案了。

3月13日
P3960 [NOIP2017 提高组] 列队(线段树上二分)
P3960 [NOIP2017 提高组] 列队(线段树上二分)
首先,对于原本就存在的点,我们不管其具体的位置,因为太多了,有 \(n^2\) 级别。
于是我们考虑只关心删除的位置。
我们对于删除一个点,其实就是相当于我们把这个位置对应点设为 0 ,然后值域线段树上的 siz-- 即可。
添加就是把对应线段树上的点设为 1 即可,顺便 siz++ 。
那么对于最后一列要特殊维护即可,我们对每一个行和最后一列开一个 vector 新加的数。
于是我们查询就变成了值域线段树上二分————第 \(k\) 小值即可。
然后小技巧就是如果这个值对应下标 \(\leq\) \(n\) ,那么直接输出原数对应的数,反则在 vector 里面找新加进来的元素。
代码如下:
#define int long long
int n,m,q,maxn;
int root[N],siz[N],ls[N],rs[N],tot;
vector<int> Ad[N];
void Modify(int &rt,int l,int r,int pos){
if(!rt) rt=++tot;
siz[rt]++;
if(l==r) return ;
int mid=l+r>>1;
if(pos<=mid) Modify(ls[rt],l,mid,pos);
else Modify(rs[rt],mid+1,r,pos);
return ;
}
int Query(int rt,int l,int r,int k){
if(l==r) return l;
int mid=l+r>>1,res=mid-l+1-siz[ls[rt]];
if(k<=res) return Query(ls[rt],l,mid,k);
return Query(rs[rt],mid+1,r,k-res);
}
int Y_Line(int x){
int pos=Query(root[n+1],1,maxn,x);
Modify(root[n+1],1,maxn,pos);
return (pos<=n)?(pos-1)*m+m:Ad[n+1][pos-n-1];
}
int X_Line(int x,int y){
int pos=Query(root[x],1,maxn,y);
Modify(root[x],1,maxn,pos);
return (pos<m)?(x-1)*m+pos:Ad[x][pos-m];
}
signed main(){
read(n),read(m),read(q);
maxn=q+max(n,m)+1;
while(q--){
int x,y;
read(x),read(y);
if(y==m){
int pos=Y_Line(x);
write(pos),puts("");
Ad[n+1].push_back(pos);
}
else{
int pos=X_Line(x,y);
write(pos),puts("");
Ad[n+1].push_back(pos);
pos=Y_Line(x);
Ad[x].push_back(pos);
}
}
return 0;
}
P3379 【模板】最近公共祖先(LCA)
ST 表维护欧拉环游序做到 \(O(nlogn)-O(1)\) 的静态在线 LCA 查询。
跑一边欧拉序,欧拉序就是我们搜索途中,每遍历到一个点就加入,每回溯到一个点也加入,然后编号构成的序列。
那么查询两点 LCA 其实就是在查询两点欧拉序上面 \(dep\) 最小的点的编号。
经典区间 RMQ 问题,使用 ST 表解决,预处理 \(O(nlogn)\) ,回答 \(O(1)\) 。
代码如下:
int Euler[N],Rev[N],dep[N],EulerCnt;
void EulerDfs(int x,int fa){
dep[x]=dep[fa]+1;
Euler[++EulerCnt]=x;
Rev[x]=EulerCnt;
for(int i=head[x];i;i=nex[i]){
int y=to[i];
if(y==fa) continue;
EulerDfs(y,x);
Euler[++EulerCnt]=x;
}
return ;
}
const int T=25;
int ST[3*N][T],Log[3*N];
void MakeST(){
for(int i=2;i<=3*n;i++) Log[i]=Log[i/2]+1;
for(int i=1;i<=EulerCnt;i++) ST[i][0]=Euler[i];
for(int j=1;j<T;j++){
for(int i=1;i+(1<<j)-1<=EulerCnt;i++){
if(dep[ST[i][j-1]]>dep[ST[i+(1<<(j-1))][j-1]]) ST[i][j]=ST[i+(1<<(j-1))][j-1];
else ST[i][j]=ST[i][j-1];
}
}
return ;
}
int QueryLCA(int x,int y){
int l=Rev[x],r=Rev[y];
if(l>r) swap(l,r);
int len=r-l+1;
if(dep[ST[l][Log[len]]]>dep[ST[r-(1<<(Log[len]))+1][Log[len]]]) return ST[r-(1<<Log[len])+1][Log[len]];
return ST[l][Log[len]];
}
CF1500A Going Home
我们观察一下发现其实序列上的一些珂技并不好用到这道题上面来,那么我们可以考虑稍微暴力一点的做法。
于是我们可以开始观察题目:题目说值域只有 \(2.5 \times 10^6\) ,和 \(n\) 相差不大,而又不需要离散化,这是为什么呢?
那么只能说明复杂度和这个值域有关了。
而复杂度和值域有关,而 \(n\) 又不大,其实我们就可以想到抽屉原理了。(我也不知道我是怎么想到的其实。)
也就是说,我们现在先把原式拆一下变成 \(a_x-a_z=a_w-a_y\) ,我们的任务就是找到两组数使得他们的差相等即可。
通过抽屉原理,我们很明显可以知道,这样的差一定会 小于等于 \(V/n\)( \(V\) 是值域 )。
于是我们枚举每一个点为起点 \(i\) ,再枚举一下公差 \(j\) 即可,我们只需要判断存不存在两个这样的数对即可。
注意还有一个特判:如果有至少两个数都出现了至少两次,那么必定有答案,也就是相当于公差为 0 。(四个一样的数也一样。)
代码如下:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=2e5+5,M=3e6+5,V=2500000;
int n,T[M],T1[M],x[M],y[M],tot,X[5],now=1;
struct node{
int val,id;
bool operator < (const node B){return val<B.val;}
}a[N];
int main(){
read(n);
for(int i=1;i<=n;i++){
read(a[i].val),a[i].id=i;
bool flag=false;
if(T[a[i].val]){
tot++;
if(tot==1) X[now++]=T[a[i].val],X[now++]=i,T[a[i].val]=0,flag=true;
else{
cout<<"Yes"<<"\n"<<X[1]<<" "<<i<<" "<<X[2]<<" "<<T[a[i].val];
return 0;
}
}
if(!flag) T[a[i].val]=i;
}
int tmp[6];
sort(a+1,a+n+1);
memset(T,0,sizeof(T));
for(int i=1;i<=n;i++) T[a[i].val]=a[i].id;
for(int i=1;i<=n;i++){
for(int j=1;j<=(int)ceil(1.0*V/n);j++){
if(T[a[i].val+j]){
if(!T1[j]) T1[j]=1,x[j]=a[i].id,y[j]=T[a[i].val+j];
else{
tmp[1]=x[j],tmp[2]=T[a[i].val+j],tmp[3]=a[i].id,tmp[4]=y[j];
sort(tmp+1,tmp+5);
if(tmp[1]==tmp[2]||tmp[2]==tmp[3]||tmp[3]==tmp[4]) continue;
puts("Yes");
cout<<x[j]<<" "<<T[a[i].val+j]<<" "<<a[i].id<<" "<<y[j];
return 0;
}
}
}
}
puts("No");
return 0;
}
关于类似复杂度为 O((V/n)*n) 的问题
其实这道题灵感来源于之前某次洛谷月赛的题目:P7273 ix35 的等差数列。
同样的,这道题也是分析一个序列两个数相邻的关系,得出了值域和个数的关系,从而让看上去很高的复杂度优化成值域线性相关的复杂度。
具体就是利用数内部之间的关系,比如洛谷那题就是利用等差数列的最后一项的性质,然后这里就是应用了抽屉原理。
3月14日
P3250 [HNOI2016]网络(线段树上二分,LCA )
P3250 [HNOI2016]网络(线段树上二分,LCA )
首先对权值做可重的离散化,然后发现题目询问的最大值满足单调性。
也就是说我们可以二分这个最大值。
由于直接判断不好判,所以其实判断等价于判断:这个值之上是不是所有权值的路径都经过了 \(x\) 。
那么我们对值域建线段树,维护每一条路径的起点和重点,判断就相当于在一个区间上判断这个值域区间上包含的所有路径的交是不是都包含 \(x\) 。
路径求交和判断一个点是不是在路径上很好做,我们可以由 LCA 的询问做到 \(O(1)\) 。
所以这就很简单了,但是这样做的复杂度是 \(O(nlog^2n)\) ,所以考虑优化。
一般像这种线段树+二分,并且线段树和二分在同一个维度上的题目(此处线段树维护值域,二分的也是值域。),其实我们都可以考虑线段树上二分。
于是这里的二分就是:对于一次查询,查询到了当前节点,如果右儿子的交集上有点 \(x\) ,那么就去左儿子,否则去右儿子。(因为要这个值尽可能大。)
代码如下:
const int N=3e6+5;
int n,m;
int head[N],nex[N<<1],to[N<<1],idx;
void add(int u,int v){
nex[++idx]=head[u];
to[idx]=v;
head[u]=idx;
return ;
}
int Euler[N],Rev[N],dep[N],EulerCnt;
void EulerDfs(int x,int fa){
dep[x]=dep[fa]+1;
Euler[++EulerCnt]=x;
Rev[x]=EulerCnt;
for(int i=head[x];i;i=nex[i]){
int y=to[i];
if(y==fa) continue;
EulerDfs(y,x);
Euler[++EulerCnt]=x;
}
return ;
}
const int T=21;
int ST[3*N][T],Log[3*N];
void MakeST(){
int t=log(EulerCnt)/log(2);
for(int i=1;i<=EulerCnt;i++) ST[i][0]=Euler[i];
for(int j=1;j<=t;j++){
for(int i=1;i+(1<<j)-1<=EulerCnt;i++){
if(dep[ST[i][j-1]]>dep[ST[i+(1<<(j-1))][j-1]]) ST[i][j]=ST[i+(1<<(j-1))][j-1];
else ST[i][j]=ST[i][j-1];
}
}
return ;
}
int QueryLCA(int x,int y){
int l=Rev[x],r=Rev[y];
if(l>r) swap(l,r);
int len=r-l+1;len=log(len)/log(2);
if(dep[ST[l][len]]>dep[ST[r-(1<<(len))+1][len]]) return ST[r-(1<<len)+1][len];
return ST[l][len];
}
struct Query{int op,u,v,w,pri;}Q[N];
int St[N<<2],Ed[N<<2];
int Cnt,tmp[5],dis[5];
struct Node{
int val,num;
bool operator < (const Node &C){return val==C.val?num<C.num:val<C.val;}
}B[N];
int tag[N<<2];
inline bool cmp(const int &a,const int &b){return dep[a]>dep[b];}
void Pushup(int x){
if(!tag[x<<1]&&!tag[x<<1|1]) return tag[x]=0,void();
tag[x]=1;
if(!tag[x<<1]) return St[x]=St[x<<1|1],Ed[x]=Ed[x<<1|1],void();
if(!tag[x<<1|1]) return St[x]=St[x<<1],Ed[x]=Ed[x<<1],void();
tmp[1]=QueryLCA(St[x<<1],St[x<<1|1]),tmp[2]=QueryLCA(St[x<<1|1],Ed[x<<1]),tmp[3]=QueryLCA(St[x<<1],Ed[x<<1|1]),tmp[4]=QueryLCA(Ed[x<<1],Ed[x<<1|1]);
sort(tmp+1,tmp+5,cmp);
if(tmp[1]!=tmp[2]) St[x]=tmp[1],Ed[x]=tmp[2];
else if(tmp[1]==QueryLCA(St[x<<1],Ed[x<<1])||tmp[1]==QueryLCA(St[x<<1|1],Ed[x<<1|1])) St[x]=Ed[x]=tmp[1];
else St[x]=Ed[x]=0;
return ;
}
void Modify(int x,int l,int r,int pos,int u,int v){
if(l==r){St[x]=u,Ed[x]=v,tag[x]=1;return ;}
int mid=(l+r)>>1;
if(pos<=mid) Modify(x<<1,l,mid,pos,u,v);
else Modify(x<<1|1,mid+1,r,pos,u,v);
Pushup(x);
return ;
}
void Change(int x,int l,int r,int pos){
if(l==r){St[x]=Ed[x]=0,tag[x]=0;return ;}
int mid=(l+r)>>1;
if(pos<=mid) Change(x<<1,l,mid,pos);
else Change(x<<1|1,mid+1,r,pos);
Pushup(x);
return ;
}
bool Check(int x,int k){
if(!St[x]&&!Ed[x]) return true;
int a=QueryLCA(St[x],Ed[x]),b=QueryLCA(k,a);
if(b!=a) return true;
if(QueryLCA(St[x],k)!=k&&QueryLCA(Ed[x],k)!=k) return true;
return false;
}
int QueryPos(int x,int l,int r,int k){
if(!tag[x]) return -1;
if(l==r){return Check(x,k)?l:-1;}
int mid=(l+r)>>1,res=-1;
if(Check(x<<1|1,k)) res=QueryPos(x<<1|1,mid+1,r,k);
if(~res) return res;
return QueryPos(x<<1,l,mid,k);
}
signed main(){
read(n),read(m);
for(int i=1,u,v;i<n;i++) read(u),read(v),add(u,v),add(v,u);
EulerDfs(1,0);
MakeST();dep[0]=INT_MAX;
for(int i=1;i<=m;i++){
int op,u,v,w;
read(op);
if(op==0){
read(u),read(v),read(w),Q[i].op=op,Q[i].u=u,Q[i].v=v,Q[i].w=w,B[++Cnt].val=w;
B[Cnt].num=Q[i].pri=i;
}
else if(op==1) read(w),Q[i].op=op,Q[i].u=w;
else read(u),Q[i].op=op,Q[i].u=u;
}
sort(B+1,B+Cnt+1);
for(int i=1;i<=m;i++) Q[B[i].num].w=i;
for(int i=1,x;i<=m;i++){
if(Q[i].op==0) Modify(1,1,Cnt,Q[i].w,Q[i].u,Q[i].v);
else if(Q[i].op==1) Change(1,1,Cnt,Q[Q[i].u].w);
else x=QueryPos(1,1,Cnt,Q[i].u),write(x==-1?x:B[x].val),putchar('\n');
}
return 0;
}
P4344 [SHOI2015]脑洞治疗仪(线段树上二分)
操作 0 就是区间赋值。
操作 1 就相当于先询问 1 个数,再区间赋值,再用 1 去赋值。
操作 2 就是询问最长子段。
操作 0 直接就是区间修改的标记,然后操作 2 重点是要多维护几个信息。(前缀最长,后缀最长之类的。)
重点是操作 1 。
其实这个过程就相当于求区间第 \(k\) 小的位置。
于是我们在线段树上二分就行了,以 \(siz\) 和 \(len\) 作为判断标准。
具体看代码实现:
int n,m,tp,l0,r0,l1,r1;
struct SegMentTree{int l,r,tot,Lmax,Rmax,tag,Max;}tr[N<<2];
inline void add(int x,int w){
tr[x].tag=w;
if(w==0) tr[x].tot=0,tr[x].Lmax=tr[x].Rmax=tr[x].Max=(tr[x].r-tr[x].l+1);
else tr[x].tot=(tr[x].r-tr[x].l+1),tr[x].Lmax=tr[x].Rmax=tr[x].Max=0;
}
inline void Pushup(int x){
tr[x].tot=tr[x<<1].tot+tr[x<<1|1].tot;
tr[x].Lmax=tr[x<<1].Lmax;tr[x].Rmax=tr[x<<1|1].Rmax;
if(tr[x<<1].Lmax==tr[x<<1].r-tr[x<<1].l+1) tr[x].Lmax+=tr[x<<1|1].Lmax;
if(tr[x<<1|1].Rmax==tr[x<<1|1].r-tr[x<<1|1].l+1) tr[x].Rmax+=tr[x<<1].Rmax;
tr[x].Max=max(max(tr[x<<1].Max,tr[x<<1|1].Max),tr[x<<1].Rmax+tr[x<<1|1].Lmax);
}
void Build(int x,int l,int r){
tr[x].l=l;tr[x].r=r;tr[x].tag=-1;
if(l==r) return tr[x].tot=1,void();
int mid=(l+r)>>1;
Build(x<<1,l,mid);Build(x<<1|1,mid+1,r);
Pushup(x);
}
inline void PushDown(int x){
if(tr[x].tag==0) add(x<<1,0),add(x<<1|1,0);
else if(tr[x].tag==1) add(x<<1,1),add(x<<1|1,1);
tr[x].tag=-1;
}
void Modify1(int x,int ql,int qr){
int l=tr[x].l,r=tr[x].r;
if(ql<=l&&r<=qr) return add(x,0),void();
int mid=(l+r)>>1;
PushDown(x);
if(ql<=mid) Modify1(x<<1,ql,qr);
if(mid<qr) Modify1(x<<1|1,ql,qr);
Pushup(x);
}
int Modify2(int x,int ql,int qr,int num){
if(!num) return 0;
int l=tr[x].l,r=tr[x].r;
if(ql<=l&&r<=qr&&num>=r-l+1-tr[x].tot){
int res=num-(r-l+1-tr[x].tot);
add(x,1);
return res;
}
int mid=(l+r)>>1;
PushDown(x);
if(ql<=mid) num=Modify2(x<<1,ql,qr,num);
if(mid<qr) num=Modify2(x<<1|1,ql,qr,num);
Pushup(x);
return num;
}
int Query1(int x,int ql,int qr){
int l=tr[x].l,r=tr[x].r;
if(ql<=l&&r<=qr) return tr[x].tot;
int mid=(l+r)>>1,res=0;
PushDown(x);
if(ql<=mid) res+=Query1(x<<1,ql,qr);
if(mid<qr) res+=Query1(x<<1|1,ql,qr);
return res;
}
SegMentTree merge(SegMentTree a,SegMentTree b){
SegMentTree res;res.l=a.l;res.r=b.r;
res.tot=a.tot+b.tot;res.Lmax=a.Lmax;res.Rmax=b.Rmax;
if(a.Lmax==a.r-a.l+1) res.Lmax+=b.Lmax;
if(b.Rmax==b.r-b.l+1) res.Rmax+=a.Rmax;
res.Max=max(max(a.Max,b.Max),a.Rmax+b.Lmax);
return res;
}
SegMentTree Query2(int x,int ql,int qr){
int l=tr[x].l,r=tr[x].r;
if(ql<=l&&r<=qr) return tr[x];
int mid=(l+r)>>1;SegMentTree a,b;a.Max=b.Max=-1;
PushDown(x);
if(ql<=mid) a=Query2(x<<1,ql,qr);
if(mid<qr) b=Query2(x<<1|1,ql,qr);
if(a.Max==-1) return b;
else if(b.Max==-1) return a;
else return merge(a,b);
}
P4364 [九省联考2018]IIIDX(线段树上二分+贪心)
P4364 [九省联考2018]IIIDX(线段树上二分+贪心)
第一步把题目抽象成一棵树。
首先我们发现,对于互不相同的情况,我们可以直接排个序就从大往小填就行了。
但是对于可重,有的时候兄弟和儿子可以互换的话,这样做就是错的。
于是我们考虑对值域建立线段树,然后每个点维护这个值之前还有多少个数可以选(包括自己)。
那么我们每次为一个点的子树预留空间其实就是可以把值大于等于这个点的全部减去一个 \(size_x\) 就行了。
然后每次对于一个点我们要选哪个就在线段树上二分找到最左边的,且在这个点之前的可以填的个数大于等于 \(size_x\) 的点(一个值)。
那么这个点的答案就是这个值。
还有记得每次到了儿子要清空父亲预留出来的贡献,但是注意只能清一次。
代码如下:
const int M=1e6+5,N=1e7+5;
#define ll long long
double k;
struct SegMentTree{int Min,add;}Tree[M<<2];
inline bool cmp(int x,int y){return x>y;}
int n,a[M],b[M],dfn[M],fa[M],siz[M],ans[M],Num[M],Pos=1,idx;
void PushUp(int x){Tree[x].Min=min(Tree[x<<1].Min,Tree[x<<1|1].Min);return ;}
void PushDown(int x){
Tree[x<<1].add+=Tree[x].add,Tree[x<<1|1].add+=Tree[x].add;
Tree[x<<1].Min+=Tree[x].add,Tree[x<<1|1].Min+=Tree[x].add;
Tree[x].add=0;
return ;
}
void Build(int x,int l,int r){
if(l==r) return Tree[x].Min=l,void();
int mid=(l+r)>>1;
Build(x<<1,l,mid),Build(x<<1|1,mid+1,r);
PushUp(x);
return ;
}
int Query(int x,int l,int r,int k){
if(l==r) return Tree[x].Min>=k?l:l+1;
PushDown(x);
int mid=(l+r)>>1;
if(k<=Tree[x<<1|1].Min) return Query(x<<1,l,mid,k);
else return Query(x<<1|1,mid+1,r,k);
}
void Modify(int x,int l,int r,int ql,int qr,int val){
if(l==ql&&r==qr) return Tree[x].Min+=val,Tree[x].add+=val,void();
PushDown(x);
int mid=(l+r)>>1;
if(qr<=mid) Modify(x<<1,l,mid,ql,qr,val);
else if(ql>mid) Modify(x<<1|1,mid+1,r,ql,qr,val);
else Modify(x<<1,l,mid,ql,mid,val),Modify(x<<1|1,mid+1,r,mid+1,qr,val);
PushUp(x);
return ;
}
int main(){
read(n);
scanf("%lf",&k);
for(int i=1;i<=n;i++) read(a[i]);
sort(a+1,a+1+n,cmp);
for(int i=n-1;i>=1;i--) Num[i]=(a[i]==a[i+1])?Num[i+1]+1:0;
for(int i=1;i<=n;i++) fa[i]=(int)floor(i/k),siz[i]=1;
for(int i=n;i>=1;i--) siz[fa[i]]+=siz[i];
Build(1,1,n);
for(int i=1,Pos;i<=n;i++){
if(fa[i]&&fa[i]!=fa[i-1]) Modify(1,1,n,ans[fa[i]],n,siz[fa[i]]-1);
Pos=Query(1,1,n,siz[i]);
Pos+=Num[Pos],Num[Pos]++,ans[i]=Pos;
Modify(1,1,n,Pos,n,-siz[i]);
}
for(int i=1;i<=n;i++) write(a[ans[i]]),putchar(' ');
return 0;
}
3月15日
P4632 [APIO2018] New Home 新家(线段树上二分)
P4632 [APIO2018] New Home 新家(线段树上二分)
首先离线询问,然后打标记,常用套路。(e.g.HH的项链)
每次询问的答案显然满足单调性,然后我们可以考虑二分答案:求得最小的 \(len\) 使得所有的颜色全部出现在区间 \([x-len,x+len]\) 当中。
于是问题变成了判断一个区间当中是否存在所有颜色,这种问题我们可以转化一下:区间后面一段的每个颜色的前缀位置的最小值在这个区间前面,则当前区间不包含所以颜色,反之则包含。
那么这个我们可以建立线段树维护最小值,然后我们每个位置的叶子结点用一个 set 维护当前位置的最小值。
要修改单点的时候修改一下前驱后继的 set 即可。
代码:
const int INF=2e8,N=9e5+5;
int n,k,q,Cnt,tot,num,root;
int Min[N*20],ls[N*20],rs[N*20],ans[N];
multiset<int> st[N],le[N*20];
struct node{int pos,T,id,op;}T[N];
inline bool cmp(const node &a,const node &b){return a.T==b.T?a.op<b.op:a.T<b.T;}
void Pushup(int x){
Min[x]=min(Min[ls[x]],Min[rs[x]]);
return;
}
void Modify(int &x,int l,int r,int pos,int v,int type){
if(!x) x=++Cnt;
if(l==r){
if(type) le[x].insert(v);
else le[x].erase(le[x].find(v));
if(!le[x].empty()) Min[x]=*le[x].begin();
else Min[x]=INF;
return ;
}
int mid=l+r>>1;
if(pos<=mid) Modify(ls[x],l,mid,pos,v,type);
else Modify(rs[x],mid+1,r,pos,v,type);
Pushup(x);
return ;
}
int Query(int pos){
if(num<k) return -1;
int l=1,r=INF,x=root,NMin,RMin=INF;
while(l<r){
int mid=l+r>>1;
NMin=min(RMin,Min[rs[x]]);
if(pos>mid||NMin<2*pos-mid) x=rs[x],l=mid+1;
else RMin=NMin,x=ls[x],r=mid;
}
return l-pos;
}
int main(){
read(n),read(k),read(q),Min[0]=INF;
for(int i=1;i<=k;i++){
st[i].insert(-INF),st[i].insert(INF);
Modify(root,1,INF,INF,-INF,1);
}
for(int i=1;i<=n;i++){
int x,id,a,b;
read(x),read(id),read(a),read(b);
T[++tot]=(node){x,a,id,1};
T[++tot]=(node){x,b+1,id,0};
}
for(int i=1;i<=q;i++){
int Pos,Time;
read(Pos),read(Time);
T[++tot]=(node){Pos,Time,i,2};
}
sort(T+1,T+tot+1,cmp);
multiset<int>::iterator a,b;
for(int i=1;i<=tot;i++){
int op=T[i].op,id=T[i].id,Pos=T[i].pos;
if(!op){
a=b=st[id].lower_bound(Pos),a--,b++;
Modify(root,1,INF,*b,Pos,0);
Modify(root,1,INF,*b,*a,1);
Modify(root,1,INF,Pos,*a,0);
if(st[id].size()==3) num--;
st[id].erase(st[id].find(Pos));
}
else if(op==1){
a=b=st[id].lower_bound(Pos),a--;
Modify(root,1,INF,*b,Pos,1);
Modify(root,1,INF,*b,*a,0);
Modify(root,1,INF,Pos,*a,1);
if(st[id].size()==2) num++;
st[id].insert(Pos);
}
else ans[id]=Query(Pos);
}
for(int i=1;i<=q;i++) write(ans[i]),putchar('\n');
return 0;
}
P6619 [省选联考 2020 A/B 卷] 冰火战士(树状数组上二分)
P6619 [省选联考 2020 A/B 卷] 冰火战士(树状数组上二分)
发现题目就是要维护一个函数的顶点。
大概长这样:
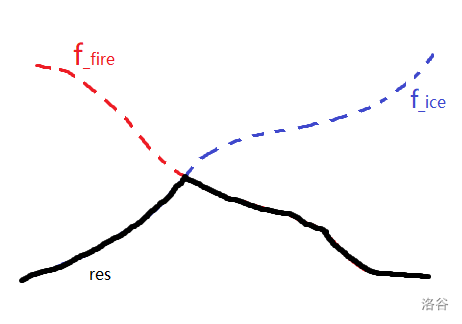
于是我们可以想到二分,但是数据太大,那么我们这里使用树状数组上二分即可。
具体见这篇题解。
P5787 二分图 /【模板】线段树分治
线段树分治板题。
主要说一下判断二分图和可撤销并查集。
判断二分图使用扩展域并查集,比如 \(x\) 向 \(y+n\) ,\(y\) 向 \(x+n\) 连边,然后判断即可。
然后因为线段树分治,所以我们回溯时要撤回操作,就使用可撤回并查集了。
具体看代码:
const int N=2e5+5,M=5e5+5;
int n,m,k,fa[M<<1],top,siz[M<<1],ans[M];
struct Back{int x,y,faX,faY,sizX,sizY;}sta[M];
struct Query{int x,y;}q[M<<2];
vector<int> Q[M<<2];
int Getfa(int x){return x==fa[x]?x:Getfa(fa[x]);}
void Return(int nowtop){while(top>nowtop) fa[sta[top].x]=sta[top].faX,fa[sta[top].y]=sta[top].faY,siz[sta[top].faX]=sta[top].sizX,siz[sta[top].faY]=sta[top].sizY,top--;return ;}
void Merge(int x,int y){
int fa1=Getfa(x),fa2=Getfa(y),siz1=siz[fa1],siz2=siz[fa2];
sta[++top].x=fa1,sta[top].y=fa2,sta[top].faX=fa[fa1],sta[top].faY=fa[fa2],sta[top].sizX=siz1,sta[top].sizY=siz2;
if(siz1>siz2) fa[fa2]=fa1,siz[fa1]+=siz[fa2];
else fa[fa1]=fa2,siz[fa2]+=siz[fa1];
return ;
}
void Modify(int x,int l,int r,int ql,int qr,int v){
if(ql<=l&&r<=qr) return Q[x].push_back(v),void();
int mid=l+r>>1;
if(ql<=mid) Modify(x<<1,l,mid,ql,qr,v);
if(qr>mid) Modify(x<<1|1,mid+1,r,ql,qr,v);
return ;
}
void DFS(int x,int l,int r){
bool flag=true;
int nowtop=top;
for(int i=0;i<Q[x].size();i++){
int a=Getfa(q[Q[x][i]].x),b=Getfa(q[Q[x][i]].y);
if(a==b){flag=false;for(int i=l;i<=r;i++) puts("No");break;}
Merge(q[Q[x][i]].x,N+q[Q[x][i]].y);
Merge(q[Q[x][i]].y,N+q[Q[x][i]].x);
if(Getfa(q[Q[x][i]].x)==Getfa(q[Q[x][i]].x+N)){flag=false;for(int i=l;i<=r;i++) puts("No");break;}
if(Getfa(q[Q[x][i]].y)==Getfa(q[Q[x][i]].y+N)){flag=false;for(int i=l;i<=r;i++) puts("No");break;}
}
if(flag){
if(l==r) puts("Yes");
else{
int mid=l+r>>1;
DFS(x<<1,l,mid);
DFS(x<<1|1,mid+1,r);
}
}
Return(nowtop);
return ;
}
int main(){
read(n),read(m),read(k);
for(int i=1;i<=n;i++) fa[i]=i,fa[i+N]=i+N,siz[i]=1,siz[i+N]=1;
for(int i=1,x,y,l,r;i<=m;i++){
read(x),read(y),read(l),read(r);
q[i].x=x,q[i].y=y;
if(l^r) Modify(1,1,k,l+1,r,i);
}
DFS(1,1,k);
return 0;
}
P4588 [TJOI2018]数学计算(线段树分治)
一个很简单的套路,对于时间建树,然后维护区间乘积,遇到除就相当于把之前的一个标记变为 1 。
代码也很简单:
const int N=2e5+5,M=5e5+5;
#define ll long long
int n,T;
ll MOD,val[N<<2];
void Pushup(int x){val[x]=val[x<<1]*val[x<<1|1]%MOD;return ;}
void Modify(int x,int l,int r,int pos,int v){
if(l==r) return val[x]=1ll*v,void();
int mid=l+r>>1;
if(pos<=mid) Modify(x<<1,l,mid,pos,v);
else Modify(x<<1|1,mid+1,r,pos,v);
Pushup(x);
return ;
}
int main(){
read(T);
while(T--){
read(n),read(MOD);
for(int i=1;i<=4*n;i++) val[i]=1;
for(int i=1,op,x;i<=n;i++){
read(op),read(x);
if(op==1) Modify(1,1,n,i,x);
else Modify(1,1,n,x,1);
write(val[1]),puts("");
}
}
return 0;
}
P5214 [SHOI2014]神奇化合物(线段树分治)
很明显的线段树分治,我们用可撤销并查集维护连通性,然后线段树分治就可以了。
修改操作也就是在时间区间上面打标记。
代码等补。
3月16日
P4585 [FJOI2015]火星商店问题(线段树分治+01Trie/可持久化Trie)
P4585 [FJOI2015]火星商店问题(线段树分治+01Trie/可持久化Trie)
先线段树离线,再上可持久化 Trie 维护异或最大和。
具体见这里。
CF576E Painting Edges(线段树分治+可撤销并查集)
CF576E Painting Edges(线段树分治+可撤销并查集)
和模板题很类似,这道题就弄 50 个图即可。
唯一要注意的是当前边不加的情况:如果不加,我们先全部假设都加了,然后到了叶子节点判断过后直接撤回即可。
具体见这里。
3月17日
P3810 【模板】三维偏序(陌上花开)
CDQ 分治 + 树状数组。
先离散化,然后 sort 第一关键字。
接下来 cdq 分治,每次先 sort 第二关键字,然后双指针+树状数组统计第三维答案。
具体见代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=2e5+5;
int top,n,m,k;
struct node{int a,b,c,num,ans;}Q[N],Q1[N];
#define ll long long
int c[N],ans[N];
void Add(int x,int v){for(;x<=k;x+=(x&(-x))) c[x]+=v;return ;}
int Ask(int x){int res=0;for(;x;x-=(x&(-x))) res+=c[x];return res;}
inline bool cmp1(node a,node b){
if(a.a==b.a){
if(a.b==b.b) return a.c<b.c;
return a.b<b.b;
}
return a.a<b.a;
}
inline bool cmp2(node a,node b){
if(a.b==b.b) return a.c<b.c;
return a.b<b.b;
}
void CDQ_Divide(int l,int r){
if(l==r) return ;
int mid=l+r>>1,tot=l;
CDQ_Divide(l,mid),CDQ_Divide(mid+1,r);
sort(Q+l,Q+mid+1,cmp2),sort(Q+mid+1,Q+r+1,cmp2);
for(int i=mid+1,j=l;i<=r;i++){
while(Q[i].b>=Q[j].b&&j<=mid) Add(Q[j].c,Q[j].num),j++,tot++;
Q[i].ans+=Ask(Q[i].c);
}
for(int i=l;i<tot;i++) Add(Q[i].c,-Q[i].num);
return ;
}
int main(){
read(n),read(k);
for(int i=1;i<=n;i++) read(Q1[i].a),read(Q1[i].b),read(Q1[i].c);
sort(Q1+1,Q1+n+1,cmp1);
for(int i=1;i<=n;i++){
top++;
if(Q1[i].a!=Q1[i+1].a||Q1[i].b!=Q1[i+1].b||Q1[i].c!=Q1[i+1].c) m++,Q[m].a=Q1[i].a,Q[m].b=Q1[i].b,Q[m].c=Q1[i].c,Q[m].num=top,top=0;
}
CDQ_Divide(1,m);
for(int i=1;i<=m;i++) ans[Q[i].ans+Q[i].num-1]+=Q[i].num;
for(int i=0;i<n;i++) write(ans[i]),putchar('\n');
return 0;
}
P2163 [SHOI2007]园丁的烦恼(二维偏序)
二维数点模型,首先转化成前缀和就是经典的二维偏序问题。
那么这里有个技巧就是把询问和修改分开来(就是用一个 op 代表 0/1 ,加点的时候相当于只会算 1 的点。)
剩下的就是直接 CDQ 分治,然后归并排序统计答案。
具体见代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=4e6+5;
int n,m,Cnt,Acnt;
#define ll long long
struct Query{
int x,y,id,op;
bool operator < (const Query &B) const{return (x==B.x)?(y==B.y?op:y<B.y):(x<B.x);}
}Q[N],tmp[N];
int Ans[N];
void CDQ_Divide(int l,int r){
if(l==r) return ;
int mid=l+r>>1;
CDQ_Divide(l,mid),CDQ_Divide(mid+1,r);
int posl=l,posr=mid+1,pos=l,tot=0;
while(posl<=mid&&posr<=r){
if(Q[posl].y<=Q[posr].y) tot+=Q[posl].op,tmp[pos++]=Q[posl++];
else Ans[Q[posr].id]+=tot,tmp[pos++]=Q[posr++];
}
while(posl<=mid) tmp[pos++]=Q[posl++];
while(posr<=r) Ans[Q[posr].id]+=tot,tmp[pos++]=Q[posr++];
for(int i=l;i<=r;i++) Q[i]=tmp[i];
return ;
}
int main(){
read(n),read(m);
for(int i=1,x,y;i<=n;i++) read(x),read(y),Q[++Cnt]=Query{x,y,0,1};
for(int i=1,a,b,c,d;i<=m;i++){
read(a),read(b),read(c),read(d);
Q[++Cnt]=Query{a-1,b-1,++Acnt,0};
Q[++Cnt]=Query{a-1,d,++Acnt,0};
Q[++Cnt]=Query{c,b-1,++Acnt,0};
Q[++Cnt]=Query{c,d,++Acnt,0};
}
sort(Q+1,Q+Cnt+1);
CDQ_Divide(1,Cnt);
for(int i=1;i+3<=Acnt;i+=4) write(Ans[i+3]+Ans[i]-Ans[i+1]-Ans[i+2]),putchar('\n');
return 0;
}
P3658 [USACO17FEB]Why Did the Cow Cross the Road III P(三维偏序)
P3658 [USACO17FEB]Why Did the Cow Cross the Road III P(三维偏序)
一个三维偏序的变种。
首先需要转化题意:相当于求 \(x_i<x_j\) 且 \(y_i>y_j\) 且 \(|z_i-z_j|>k\) 的点对 \((i,j)\) 的数量。
然后就变成了三维偏序问题,但是这里有个问题就是第三个条件。
显然对于 \(i\) 来说就是 \([1,z_i-k-1]\) 和 \([z_i+k+1,n]\) 的点 \(j\) 的个数。
于是我们把这一维可以放在第三维上面,然后在用树状数组统计的时候我们可以这样询问:\(Query(z_i-k-1)+Query(n)-Query(z_i+k)\) 。
然后就是模板了。
代码如下:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=2e5+5;
int n,m,k,Cnt,Acnt,b[N],c[N];
#define ll long long
struct Query{
int x,y,z,id;
bool operator < (const Query &B) const{return (x==B.x)?((y==B.y)?(z<B.z):(y>B.y)):(x<B.x);}
}Q[N];
ll Ans;
void Add(int x,int v){for(;x<=n;x+=(x&(-x))) c[x]+=v;}
int Ask(int x){int res=0;for(;x;x-=(x&(-x))){res+=c[x];}return res;}
inline bool cmp2(Query x,Query y){return x.y==y.y?x.z<y.z:x.y>y.y;}
void CDQ_Divide(int l,int r){
if(l==r) return ;
int mid=l+r>>1,tot=l;
CDQ_Divide(l,mid),CDQ_Divide(mid+1,r);
sort(Q+l,Q+mid+1,cmp2),sort(Q+mid+1,Q+r+1,cmp2);
for(int i=mid+1,j=l;i<=r;i++){
while(Q[i].y<=Q[j].y&&j<=mid) Add(Q[j].z,1),j++,tot++;
Ans+=Ask(max(Q[i].z-k-1,0))+Ask(n)-Ask(min(Q[i].z+k,n));
}
for(int i=l;i<tot;i++) Add(Q[i].z,-1);
return ;
}
int main(){
read(n),read(k);
for(int i=1,x;i<=n;i++) read(x),b[x]=i;
for(int i=1,x;i<=n;i++) read(x),Q[i]=Query{b[x],i,x};
sort(Q+1,Q+n+1);
CDQ_Divide(1,n);
write(Ans);
return 0;
}
如果类似第三维的限制有两维,甚至三维呢?
待解。
P4093 [HEOI2016/TJOI2016]序列(cdq 分治 + dp)
P4093 [HEOI2016/TJOI2016]序列(cdq 分治 + dp)
三维偏序 + dp。
这道题有两个值得学习的点:
\(1.\) 三维偏序这里的偏序不是维度一一对应的,而是交叉的,这道题的偏序关系其实就是:\(Max_i \leq a_j\) 和 \(a_i \leq Min_j\) 以及 \(i<j\) 。
\(2.\) 这里是三维偏序优化 dp ,所以相对于平常的三维偏序写法有点变化,大概是先分治左半,然后直接处理跨越的,最后再还原后分治右半。
至于更新就是维护一下 dp 数组,树状数组来维护 Max 即可。
代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=2e5+5;
int n,m,k,Cnt,Acnt,c[N],dp[N],Ans;
#define ll long long
struct Query{
int x,y,z,id;
}Q[N];
void Add(int x,int v){for(;x<=n;x+=(x&(-x))) c[x]=max(c[x],v);}
int Ask(int x){int res=0;for(;x;x-=(x&(-x))){res=max(res,c[x]);}return res;}
void Clear(int x){for(;x<=n;x+=(x&(-x))) c[x]=0;return ;}
inline bool CmpMax(Query x,Query y){return x.z<y.z;}
inline bool CmpMin(Query x,Query y){return x.y<y.y;}
inline bool CmpVal(Query x,Query y){return x.x<y.x;}
inline bool CmpId(Query x,Query y){return x.id<y.id;}
void CDQ_Divide(int l,int r){
if(l==r){dp[l]=max(dp[l],1);return ;}
int mid=l+r>>1,tot=l;
CDQ_Divide(l,mid);
sort(Q+l,Q+mid+1,CmpMax),sort(Q+mid+1,Q+r+1,CmpVal);
for(int i=mid+1,j=l;i<=r;i++){
while(Q[i].x>=Q[j].z&&j<=mid) Add(Q[j].x,dp[Q[j].id]),j++,tot++;
dp[Q[i].id]=max(dp[Q[i].id],Ask(Q[i].y)+1);
}
for(int i=l;i<tot;i++) Clear(Q[i].x);
sort(Q+mid+1,Q+r+1,CmpId);
CDQ_Divide(mid+1,r);
return ;
}
int main(){
read(n),read(m);
for(int i=1;i<=n;i++) read(Q[i].x),Q[i].id=i,Q[i].z=Q[i].y=Q[i].x;
for(int i=1,x,v;i<=m;i++){
read(x),read(v);
Q[x].y=min(Q[x].y,v);
Q[x].z=max(Q[x].z,v);
}
CDQ_Divide(1,n);
for(int i=1;i<=n;i++) Ans=max(Ans,dp[i]);
write(Ans);
return 0;
}
BS4744【BZOJ1123】四维偏序
四维偏序模板。
cdq + cdq + 树状数组。
大概就是对于第一维打上 \(L/R\) 标记,然后对剩下三维搞普通的三维偏序。
容易发现只有当 \((L,L,z_i,d_i)\) 才有可能对 \((R,R,z_j,d_j)\) 产生贡献。
具体见代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=2e5+5,LEFT=-1,RIGHT=1;
int n,m,k,Cnt,Acnt,c[N];
#define ll long long
ll Ans;
struct Query{int d1,d2,d3,d4,part,val;}Q[N],Q1[N],Q2[N];
void Add(int x,int v){for(;x<=n;x+=(x&(-x))) c[x]+=v;}
int Ask(int x){int res=0;for(;x;x-=(x&(-x))) res+=c[x];return res;}
void Clear(int x){for(;x<=n;x+=(x&(-x))) c[x]=0;return ;}
inline bool CmpD1(Query a,Query b){return a.d1<b.d1;}
inline bool CmpD2(Query a,Query b){return a.d2<b.d3;}
inline bool CmpD3(Query a,Query b){return a.d3<b.d3;}
inline bool CmpD4(Query a,Query b){return a.d4<b.d4;}
void CDQ_Divide_3D(int l,int r){
if(l==r) return ;
int mid=l+r>>1;
CDQ_Divide_3D(l,mid),CDQ_Divide_3D(mid+1,r);
int posl=l,posr=mid+1,pos=l;
while(posl<=mid&&posr<=r){
if(Q1[posr].d3>=Q1[posl].d3){
if(Q1[posl].part==LEFT) Add(Q1[posl].d4,Q1[posl].val);
Q2[pos++]=Q1[posl++];
}
else{
if(Q1[posr].part==RIGHT) Ans+=Ask(Q1[posr].d4);
Q2[pos++]=Q1[posr++];
}
}
while(posl<=mid) Q2[pos++]=Q1[posl++];
while(posr<=r){
if(Q1[posr].part==RIGHT) Ans+=Ask(Q1[posr].d4);
Q2[pos++]=Q1[posr++];
}
for(int i=l;i<=r;i++){
if(Q2[i].part==LEFT) Clear(Q2[i].d4);
Q1[i]=Q2[i];
}
return ;
}
void CDQ_Divide_2D(int l,int r){
if(l==r) return ;
int mid=l+r>>1;
CDQ_Divide_2D(l,mid),CDQ_Divide_2D(mid+1,r);
int posl=l,posr=mid+1,pos=l;
while(posl<=mid&&posr<=r){
if(Q[posr].d2>=Q[posl].d2) Q[posl].part=LEFT,Q1[pos++]=Q[posl++];
else Q[posr].part=RIGHT,Q1[pos++]=Q[posr++];
}
while(posl<=mid) Q[posl].part=LEFT,Q1[pos++]=Q[posl++];
while(posr<=r) Q[posr].part=RIGHT,Q1[pos++]=Q[posr++];
for(int i=l;i<=r;i++) Q[i]=Q1[i];
CDQ_Divide_3D(l,r);
return ;
}
int main(){
read(n);
for(int i=1;i<=n;i++) Q[i].d1=i,Q[i].val=1;
for(int i=1;i<=n;i++) read(Q[i].d2);
for(int i=1;i<=n;i++) read(Q[i].d3);
for(int i=1;i<=n;i++) read(Q[i].d4);
CDQ_Divide_2D(1,n);
write(Ans);
return 0;
}



