色々ソート
十大经典排序算法
分类
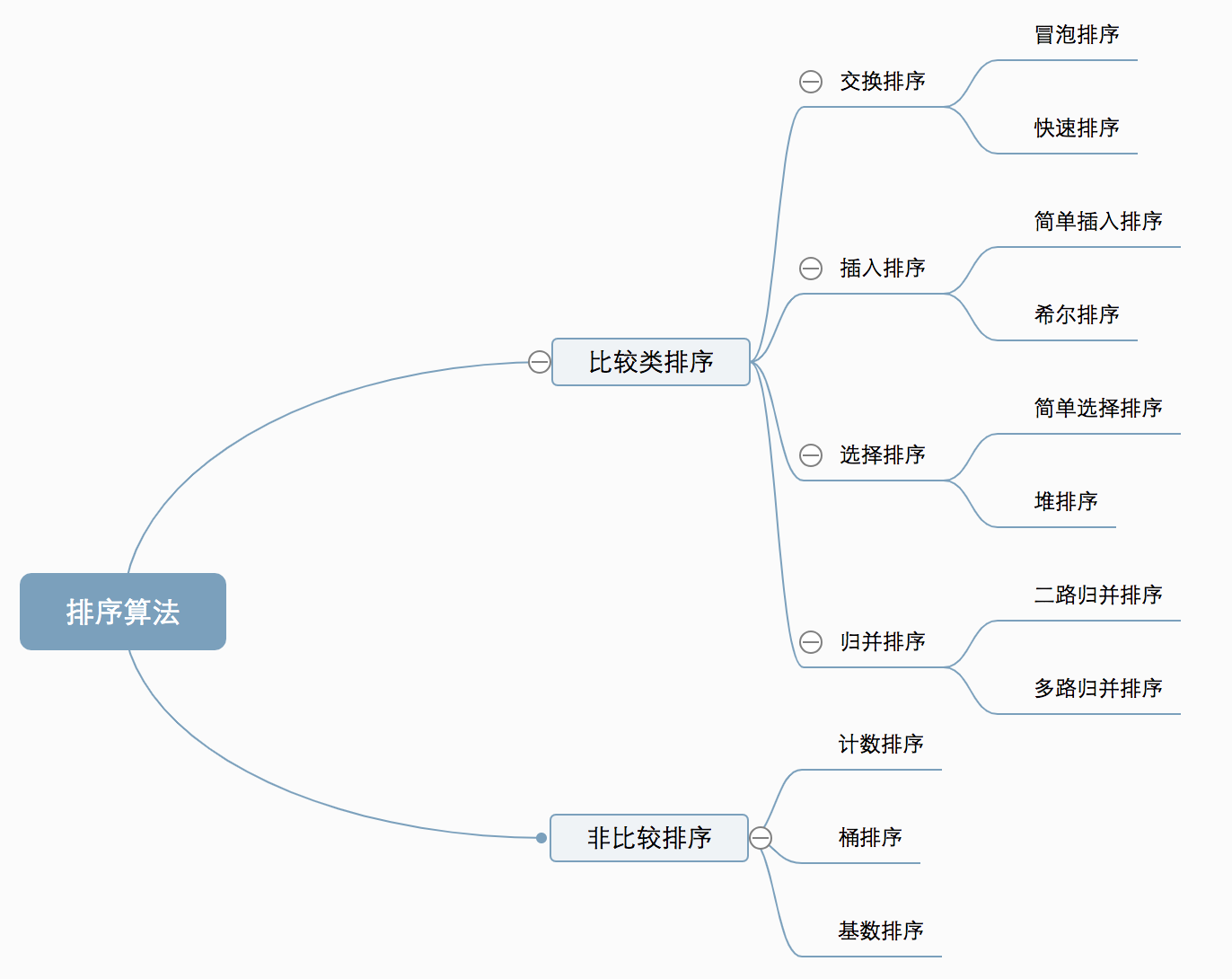
十大常见排序算法可分为两大类:
- 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
- 非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
复杂度

- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
- 不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
算法详解
代码原型
C++
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
void inSortName();
void putIn();
void putOut();
int num, len;
vector<int>v; //代排序数组
vector<string> sort_name; //算法名字储存数组
vector<void(*)()> v_func; //Or:vector<function<void()>> v_func
...//十个排序算法函数,具体见后文
void doQuickSort(){ //启动器
len = v.size();
quickSort(0, len-1);
}
//堆排序
int main(){
inSortName();
putIn();
putOut();
return 0;
}
void inSortName(){
sort_name.push_back("Bubble Sort");
sort_name.push_back("Selection Sort");
sort_name.push_back("Insertion Sort");
sort_name.push_back("Shell Sort");
sort_name.push_back("Merge Sort");
sort_name.push_back("Quick Sort");
sort_name.push_back("Heap Sort");
sort_name.push_back("Counting Sort");
sort_name.push_back("Bucket Sort");
sort_name.push_back("Radix Sort");
v_func.push_back(bubbleSort);
v_func.push_back(selectionSort);
v_func.push_back(insertionSort);
v_func.push_back(shellSort);
v_func.push_back(doMergeSort);
v_func.push_back(doQuickSort);
v_func.push_back(heapSort);
v_func.push_back(countingSort);
v_func.push_back(bucketSort);
v_func.push_back(radixSort);
}
void putIn(){
for(int i = 0; i < sort_name.size(); i++){
cout << i+1 << "." << sort_name[i] << endl;
}
cout << "请输入数字选择排序算法:" << endl;
int sort_index;
cin >> sort_index;
cout << "\n请输入待排序数组以空格隔开, Ctrl+z结束:\n";
v.clear();
while(cin >> num){
v.push_back(num);
}
v_func[sort_index-1](); //有参数在括号中加上即可
}
void putOut(){
for(int i = 0; i < len-1; i++){
cout << v[i] << " ";
}
cout << v[len-1] << endl;
}
Java
import java.lang.reflect.InvocationTargetException;
import java.lang.reflect.Method;
import java.util.Scanner;
import java.util.Vector;
class Sort {
private static Vector<Integer> v = new Vector<>();
private static int len, num, testTime = 0;
...//十大排序算法
public void putIn() {
Scanner in = new Scanner(System.in);
v.clear();
System.out.println("\n请输入待排序数组以空格隔开,Ctrl+D结束:");
//输入任意数量的整数,Ctrl+D表示Eof
while (in.hasNext()) {
num = in.nextInt();
v.add(num);
}
}
public void putOut() {
for (int i = 0; i < len - 1; i++) {
System.out.printf("%d ", v.get(i));
}
System.out.printf("%d\n", v.get(len - 1));
}
public void swap(int x, int y) {
int temp;
temp = v.get(x);
v.set(x, v.get(y));
v.set(y, temp);
}
}
public class Main {
private static int sortIndex;
//算法名容器
private static Vector<String> sortName = new Vector<>();
//算法函数选择容器
private static Vector<String> vFunc = new Vector<>();
private static Scanner in = new Scanner(System.in);
private static Sort st = new Sort();
public static void main(String[] args) throws NoSuchMethodException, IllegalAccessException, InvocationTargetException {
sortNameList();
selectSort();
st.putIn();
doSort();
st.putOut();
}
private static void sortNameList() {
sortName.add("Bubble Sort");
sortName.add("Selection Sort");
sortName.add("Insertion Sort");
sortName.add("Shell Sort");
sortName.add("Merge Sort");
sortName.add("Quick Sort");
sortName.add("Heap Sort");
sortName.add("Counting Sort");
sortName.add("Bucket Sort");
sortName.add("Radix Sort");
vFunc.add("bubbleSort");
vFunc.add("selectionSort");
vFunc.add("insertionSort");
vFunc.add("shellSort");
vFunc.add("doMergeSort");
vFunc.add("doQuickSort");
vFunc.add("heapSort");
vFunc.add("countingSort");
vFunc.add("bucketSort");
vFunc.add("radixSort");
}
private static void selectSort() {
int i = 0;
for (String s :
sortName) {
System.out.printf("%d.%s.\n", ++i, s);
}
System.out.printf("请输入数字选择排序算法:\n");
sortIndex = in.nextInt() - 1;
}
private static void doSort() throws NoSuchMethodException, InvocationTargetException, IllegalAccessException {
Method method = st.getClass().getMethod(vFunc.get(sortIndex), new Class[0]);
method.invoke(st, new Object[0]);
}
}
冒泡排序(Bubble Sort)
比较相邻元素,大的向后交换
算法思路
- 从前往后比较每对相邻元素,将大的元素向后交换。(每次比较完成将得到未排序队列中最大的数排在已排序队列前端)
- 重复N-1次步骤1,所有元素都完成了从小到大的排序。
图解

代码
C++
//冒泡排序
void bubbleSort(){
len = v.size();
for(int i = 0; i < len-1; i++){
for(int j = 0; j < len-1-i; j++){
if(v[j] > v[j+1]){
swap(v[j], v[j+1]);
}
}
}
}
Java
//冒泡排序
public void bubbleSort() {
len = v.size();
for (int i = 0; i < len - 1; i++) {
for (int j = 0; j < len - 1 - i; j++) {
int a = v.get(j), b = v.get(j + 1);
if (a > b) swap(j, j + 1);
}
}
}
选择排序(Selection Sort)
不断选择最小(大)元素往前放
因为无论什么数据时间复杂度都是O(n2),表现最稳定的排序算法之一。
算法思路
- 从未排序的队列中找到最小(大)元素,存放到排序序列的起始位置;
- 再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾;
- 以此类推,直到所有元素均排序完毕。
图解
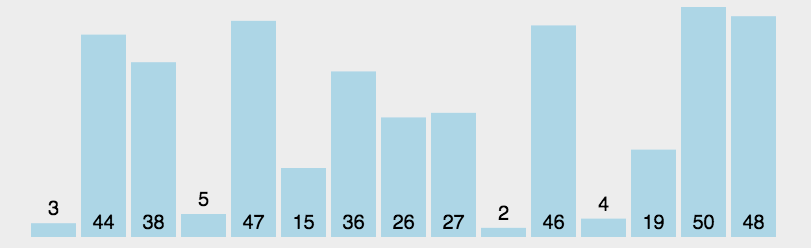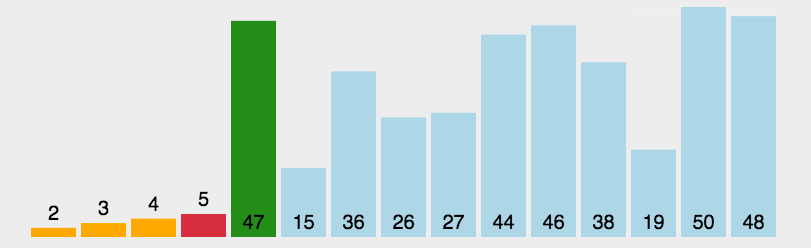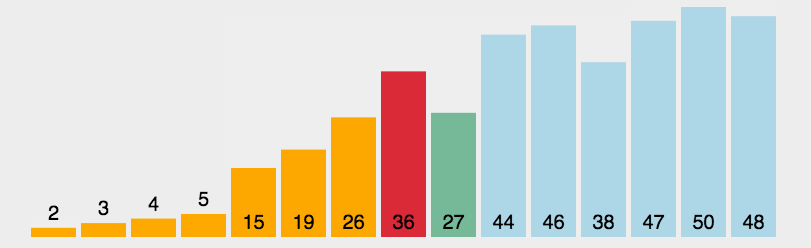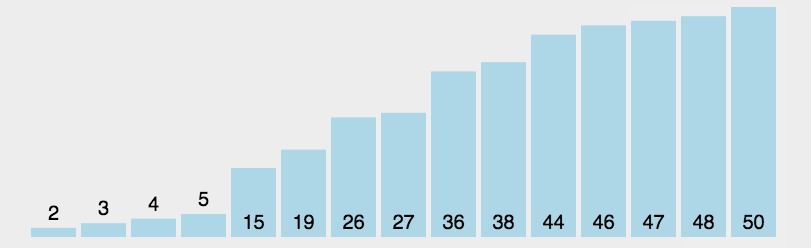
代码
C++
//选择排序
void selectionSort(){
int min_num;
len = v.size();
for(int i = 0; i < len-1; i++){
min_num = i;
for(int j = i+1; j < len; j++){
if(v[j] < v[min_num]){
min_num = j;
}
}
swap(v[min_num], v[i]);
}
}
Java
//选择排序
public void selectionSort() {
int minNum;
len = v.size();
for (int i = 0; i < len - 1; i++) {
minNum = i;
for (int j = i + 1; j < len; j++) {
int a = v.get(minNum), b = v.get(j);
if (a > b) {
minNum = j;
}
}
swap(i, minNum);
}
}
插入排序(Insertion Sort)
将未排序元素插入到排序队列中
算法思路
- 第一个元素被认为已排序序列;
- 取出下一个元素,在已排序元素序列中扫描插入合适位置。
注意
插入排序通常采用in-place排序(即原位操作,不允许使用临时变量),所以定义两个数组等操作不可取。
图解

代码
C++
//插入排序
void insertionSort(){
len = v.size();
int index, current_num;
for (int i = 1; i < len; i++){
index = i;
current_num = v[i];
while(index-1 >= 0 && v[index-1] > current_num){
v[index] = v[index-1];
index--;
}
v[index] = current_num;
}
}
Java
//插入排序
public void insertionSort(){
int index, currentNum;
len = v.size();
for (int i = 1; i < len; i++) {
index = i;
currentNum = v.get(i);
while (index-1 >= 0 && v.get(index-1) > currentNum){
v.set(index, v.get(index-1));
index--;
}
v.set(index, currentNum);
}
}
希尔排序(Shell Sort)
插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序
算法思路
- 设置一个增量,一般 gap = length/2;
- 将队列按增量进行分组,对每组进行单独的直接插入排序;
- 缩小增量 gap = gap/2;
- 重复步骤2,3,直到gap = 1时,排序完成。
算法讲解
希尔排序首先设置一个初始增量,我们一般采用gap = length/2为初始增量(此时缩小增量为gap=gap/2),这是希尔建议的增量,被称为希尔增量,这个增量并不是最优的。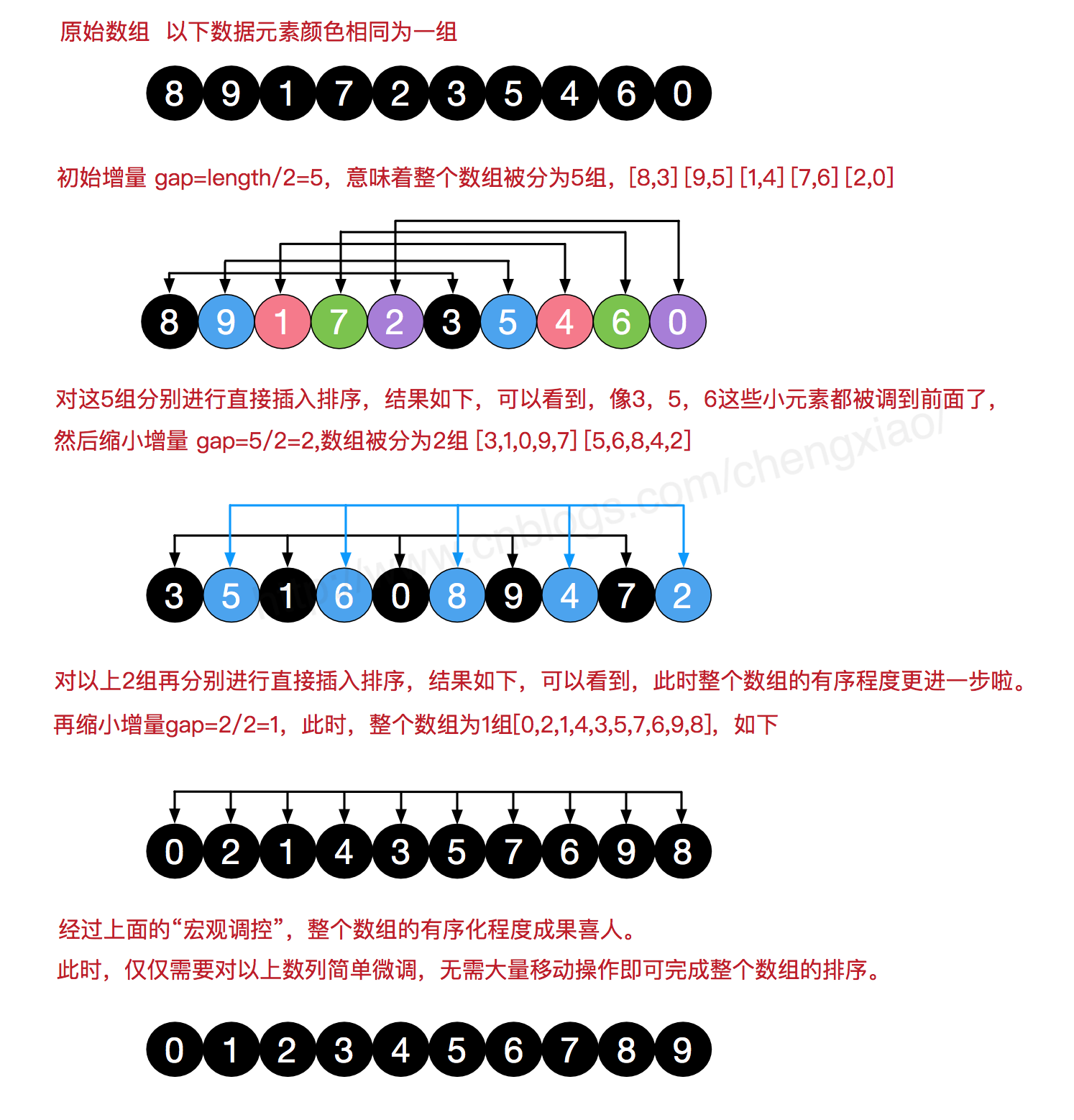
代码
C++
//希尔排序
void shellSort(){
int index, current_num;
len = v.size();
for (int gap = len/2; gap > 0; gap /= 2){
for (int i = gap; i < len; i++){
int index = i;
current_num = v[i];
while(index - gap >= 0 && current_num < v[index-gap]) {
v[index] = v[index-gap];
index -= gap;
}
v[index] = current_num;
}
}
}
java
//希尔排序
public void shellSort(){
int index, currentNum;
len = v.size();
for (int gap = len/2; gap > 0; gap /= 2) {
for (int i = gap; i < len; i++) {
index = i;
currentNum = v.get(i);
while (index-gap >= 0 && v.get(index-gap) > currentNum){
v.set(index, v.get(index-gap));
index -= gap;
}
v.set(index, currentNum);
}
}
}
算法分析
从代码上看,其实就是插入排序上多了一个增量的循环。
核心在于间隔序列的设定。既可以提前设定好间隔序列,也可以动态的定义间隔序列。
归并排序(Merge Sort)
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。将两个有序表合并成一个有序表,称为2-路归并。
算法思路
- 把长度为n的待排序序列分为两个长度n/2的子序列;
- 对这两个子序列继续采用第一步;
- 将排序号的子序列进行合并排序为一个排序好的序列;
- 重复直到得到长度为n的序列。
注意:当子序列长度为1时,就一定是排序好的序列。
图解
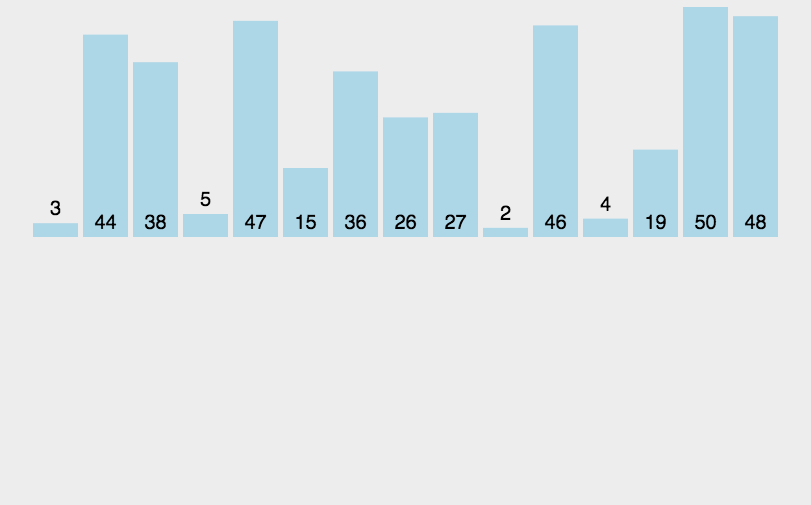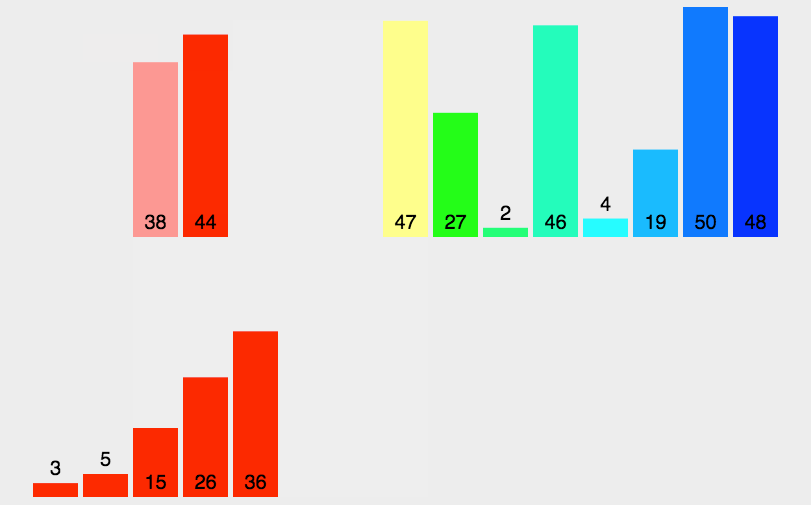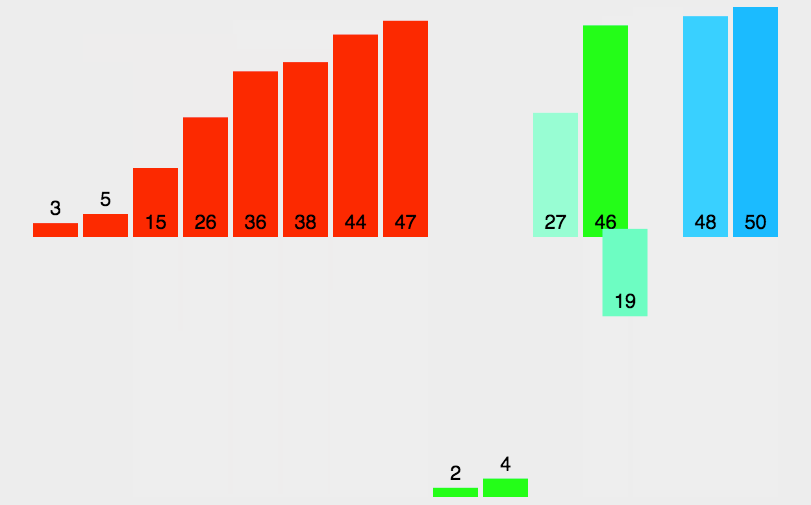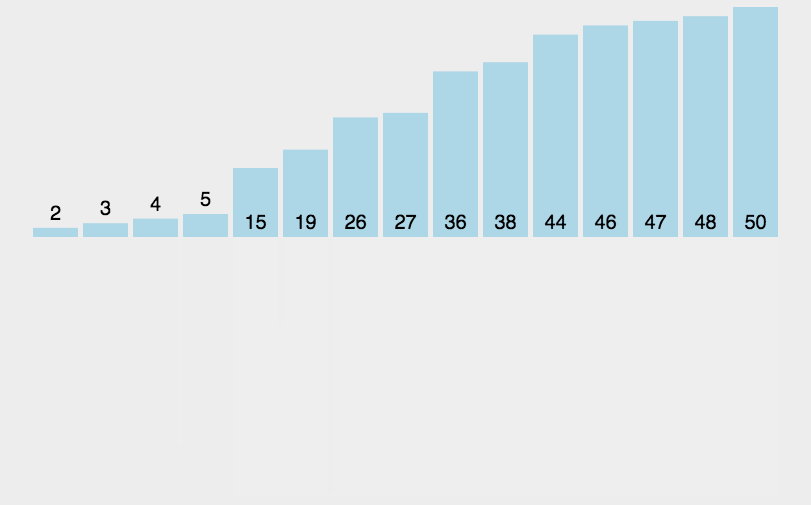
代码
将待排序序列传入mergeSort()。mergeSort会把序列一分为二,然后采用递归思路再次对左右序列进行一分为二,直到每个序列长度为1为止,此时单个序列必定有序。merge()函数会对一分为二的序列进行重新排序组合,能把两个有序序列排列为一个有序序列。
C++
//归并排序
vector<int> merge(vector <int> left, vector <int> right){
vector <int> result;
while(left.size() > 0 && right.size() > 0){
if(left[0] <= right[0]){
result.push_back(left[0]);
left.erase(left.begin());
}else{
result.push_back(right[0]);
right.erase(right.begin());
}
}
while(left.size()){
result.push_back(left[0]);
left.erase(left.begin());
}
while(right.size()){
result.push_back(right[0]);
right.erase(right.begin());
}
return result;
}
vector<int> mergeSort(vector <int> ary){
int len_merge = ary.size();
if(len_merge < 2) return ary;
int mid = len_merge/2;
vector <int> left(ary.begin(), ary.begin()+mid), right(ary.begin()+mid, ary.begin()+len_merge);
return merge(mergeSort(left), mergeSort(right));
}
Java
//归并排序
public Vector<Integer> merge(Vector<Integer> left, Vector<Integer> right) {
Vector<Integer> result = new Vector<>();
while (left.size() > 0 && right.size() > 0) {
if (left.get(0) <= right.get(0)) {
result.add(left.remove(0));
;
} else {
result.add(right.remove(0));
}
}
while (left.size() > 0) result.add(left.remove(0));
while (right.size() > 0) result.add(right.remove(0));
return result;
}
public Vector<Integer> mergeSort(Vector<Integer> ary) {
/*System.out.printf("%d:%s\n", testTime++, ary);*/
int mergeLen = ary.size();
if (mergeLen < 2) return ary;
int mid = mergeLen / 2;
Vector<Integer> left = new Vector<>();
Vector<Integer> right = new Vector<>();
int i = 0;
while (i < mid) {
left.add(ary.get(i++));
}
while (i < mergeLen) {
right.add(ary.get(i++));
}
return merge(mergeSort(left), mergeSort(right));
}
算法分析
归并排序是一种稳定的排序方法。和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(nlogn)的时间复杂度。代价是需要额外的内存空间
快速排序(Quick Sort)
通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
快速排序思路依旧来源于分治法。
算法思路
- 从序列中挑一个元素作为"基准数";
- 重排序列,将比基准小的元素放在基准数前,大的元素放在基准数后面。
- 对两边子序列使用递归重复1、2步。
图解
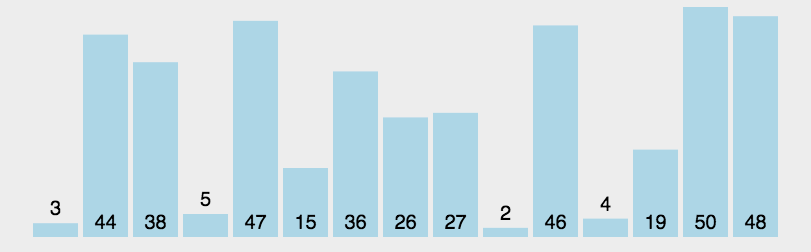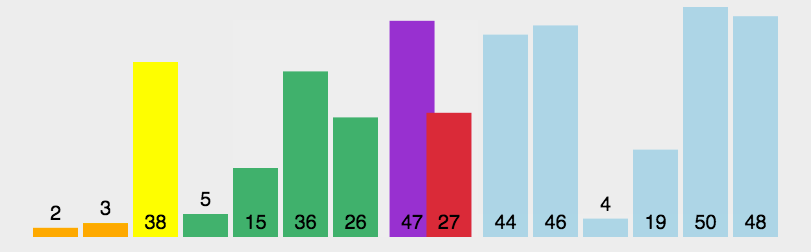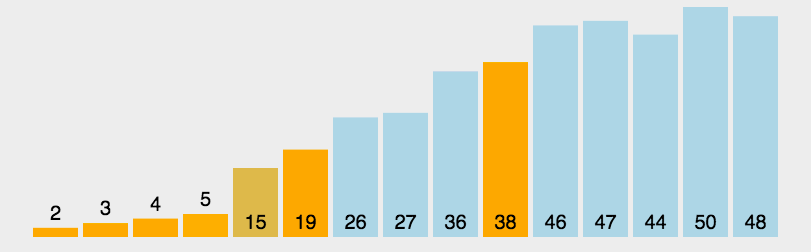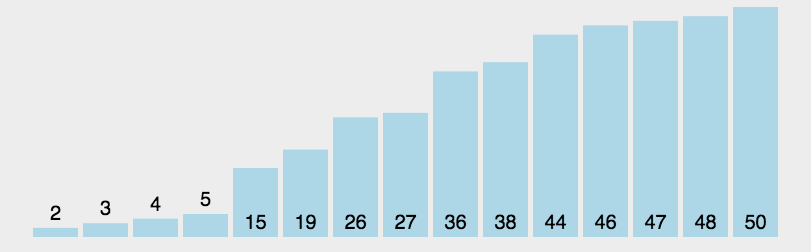
代码
v为待排序序列。对每个进行快排的(子)序列,以最左边的数为基准数,找到一个位置保证左边元素小于基准数,右边元素大于基准数。
C++
//快速排序 开始left=0 right=len-1
void quickSort(int left, int right){
if(left >= right) return;
int i = left, j = right, base = v[left];
while(i < j) {
while (v[j] >= base && i < j) j--;
while (v[i] <= base && i < j) i++;
if(i < j){
swap(v[i], v[j]);
}
}
v[left] = v[i];
v[i] = base;
quickSort(left, i-1);
quickSort(i+1, right);
}
Java
//快速排序
public void quickSort(int left, int right) {
if (left >= right) return;
int i = left, j = right, base = v.get(left);
while (i < j) {
while (v.get(j) >= base && i < j) j--;
while (v.get(i) <= base && i < j) i++;
if (i < j) swap(i, j);
}
v.set(left, v.get(i));
v.set(i, base);
quickSort(left, i - 1);
quickSort(i + 1, right);
}
堆排序(Heap Sort)
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
算法思路
- 将代排序列构成大顶堆(大顶堆构建思路就是对树的所有根节点,从下往上对每个根节点和他的两个或更少的节点进行比较,将其中对大的元素放在根节点位置上)
- 将堆(树)顶R[1]元素和最后一个R[n]元素进行交换。
- 对新的无序序列(R[1]...R[n-1])重复上述两步。
图解

代码
C++
//堆排序
void adjustHeap(int i){
int left = 2*i+1, right = 2*i+2;
int max_point = i;
if(left < len && v[left] > v[max_point]) max_point = left;
if(right < len && v[right] > v[max_point]) max_point = right;
if(max_point != i){
swap(v[i], v[max_point]);
adjustHeap(max_point);
}
}
void buildMaxHeap(){
len = v.size();
for(int i = len/2; i >=0; i--) adjustHeap(i);
}
void heapSort(){
buildMaxHeap();
for(int i = v.size()-1; i > 0; i--){
swap(v[0], v[i]);
len--;
adjustHeap(0);
}
len = v.size();
}
Java
//堆排序
public void adjustHeap(int i) {
int left = 2 * i + 1, right = 2 * i + 2; //二叉树子节点公式
int maxPoint = i;
if (left < len && v.get(left) > v.get(maxPoint)) maxPoint = left;
if (right < len && v.get(right) > v.get(maxPoint)) maxPoint = right;
if (maxPoint != i) {
swap(i, maxPoint);
adjustHeap(maxPoint);
}
}
public void buildMaxHeap() {
len = v.size();
for (int i = len / 2; i >= 0; i--) adjustHeap(i); //二叉树根节点 <= 叶子节点
}
public void heapSort() {
buildMaxHeap();
for (int i = v.size() - 1; i > 0; i--) {
swap(0, i);
len--;
adjustHeap(0);
}
len = v.size();
}
计数排序(Counting Sort)
计数排序思想很简单,从待排序序列找出最大和最小的数,在这个范围统计每个数出现的次数。计数排序不再是基于比较的排序,作为一种线性时间复杂度的排序,排序速度快于任何比较排序算法。当k不是很大并且序列比较集中时,计数排序是一个很有效的排序算法。
计数排序有基础班、优化版、进阶版等,整体思想不变,只是会在节约空间等方面做出更复杂的计算,一下提供进阶版思路。
算法思路
- 创建一个新数组Count,大小为待排序序列MaxNum-MinNum+1.创建一个数组(队列)result存储排序后队列。
- 以待排序序列中数值Value-MinNum为Key,在Count数组中进行计数处理。
- 对Count数组进行累加求和:count[i] += count[i - 1],此时Count中存储的就是每个数字在result数组中对应的位置(相同数位置下移)
- 根据Count数组中对应位置对result数组进行赋值。
图解
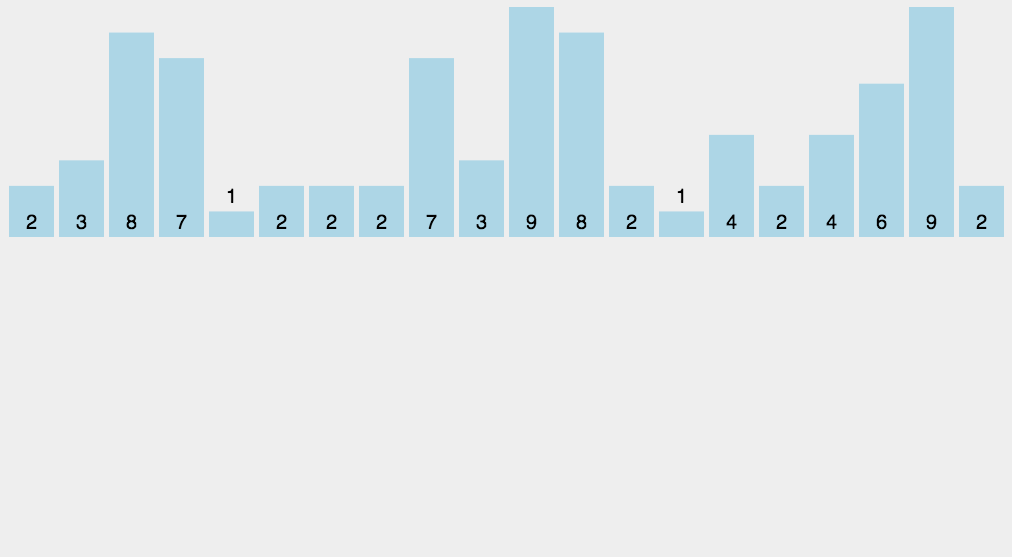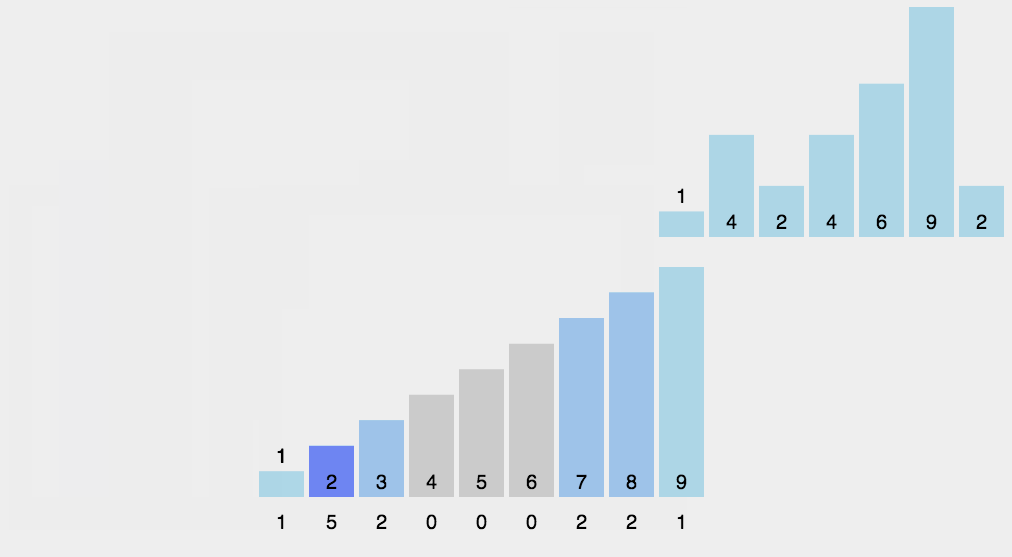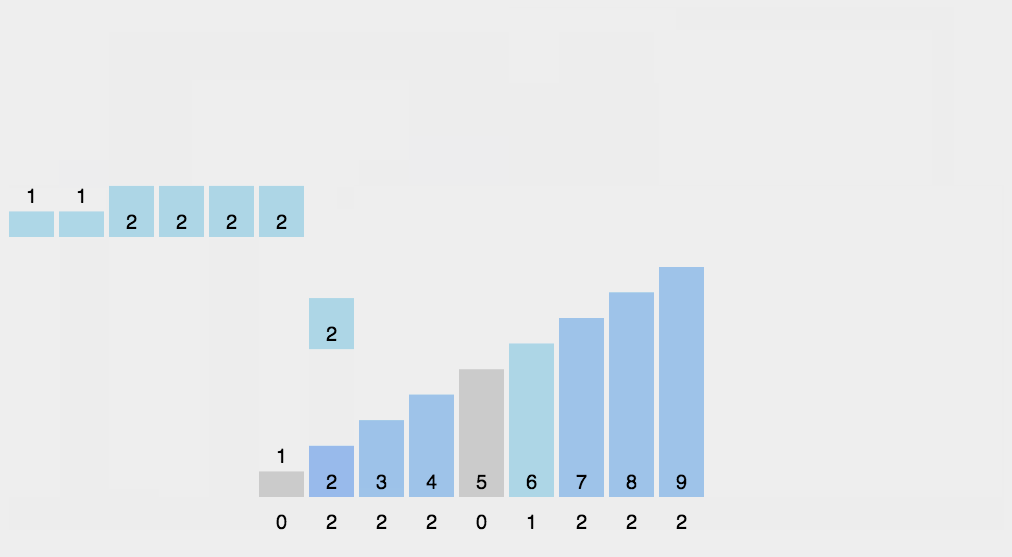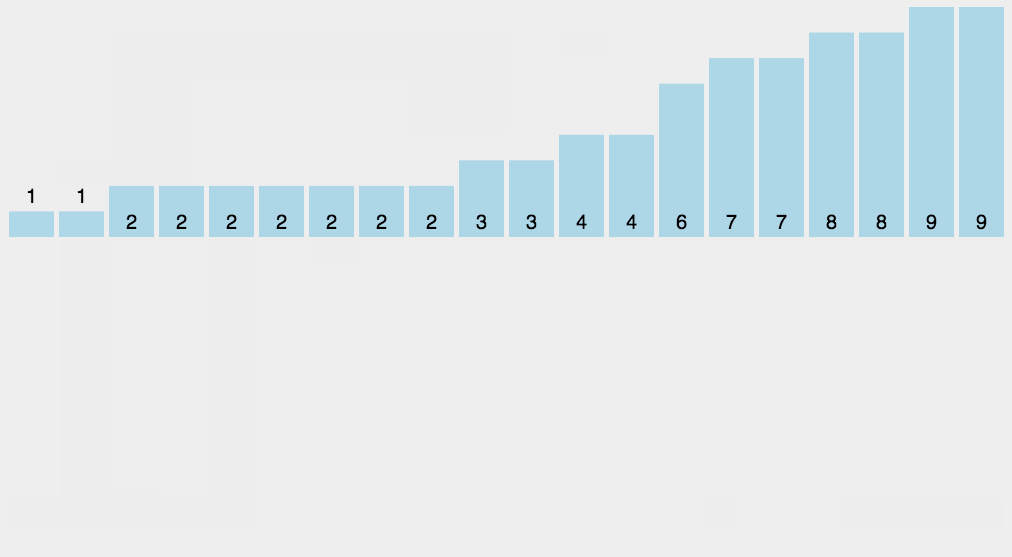
代码
C++
//计数排序
void countingSort() {
int max_num = *max_element(v.begin(), v.end()), min_num = *min_element(v.begin(), v.end());
len = v.size();
vector<int> result(len);
int count_size = max_num - min_num + 1;
int *count = new int[count_size];
memset(count, 0, sizeof(count)*count_size);
for (int i = 0; i < len; i++) {
count[v[i] - min_num]++;
}
for (int i = 1; i < count_size; i++) {
count[i] += count[i - 1];
}
for (int i = 0; i < len; i++){
result[count[v[i] - min_num] - 1] = v[i];
count[v[i] - min_num]--;
}
v = result;
}
Java
//计数排序
public void countingSort() {
int maxNum = Collections.max(v), minNum = Collections.min(v);
len = v.size();
Vector<Integer> vv = new Vector<Integer>();
vv.setSize(len);
int countSize = maxNum - minNum + 1;
int count[] = new int[countSize];
Arrays.fill(count, 0);
for (int i = 0; i < len; i++) {
count[v.get(i) - minNum]++;
}
for (int i = 1; i < countSize; i++) {
count[i] += count[i-1];
}
for (int i = 0; i < len; i++) {
vv.set(count[v.get(i)-minNum] - 1, v.get(i));
count[v.get(i) - minNum]--;
}
v = vv;
}
算法分析
计数排序是一个稳定的排序算法。当输入的元素是 n 个 0到 k 之间的整数时,时间复杂度是O(n+k),空间复杂度也是O(n+k),其排序速度快于任何比较排序算法。当是因为消耗空间巨大所以指在K不大且序列较集中时才是个有效的排序算法。
桶排序(Bucket Sort)
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排)。
算法思路
- 设置一个定量作为桶容量;
- 根据 ((maxNum - minNum) / bucketSize) + 1 求得所需桶的数量;
- 遍历数据,把所有数据放入对应桶里;
- 对每个桶单独排序;
- 把所有桶数据拼接起来。
图解
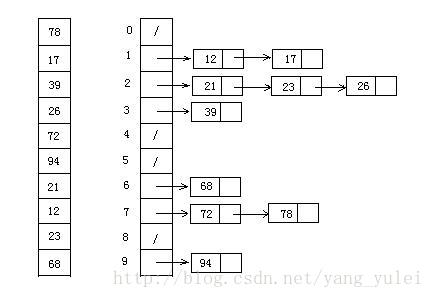
代码
C++
void bucketSort() {
int i, j, max_num = *max_element(v.begin(), v.end()), min_num = *min_element(v.begin(), v.end());
const int bucket_size = 5; //桶容量
int bucket_count = ((max_num - min_num) / bucket_size) + 1; //桶个数
vector<int> *buckets = new vector<int>[bucket_count];
vector<int> result;
for (i = 0; i < v.size(); i++) {
buckets[(v[i] - min_num) / bucket_size].push_back(v[i]);
}
for (i = 0; i < bucket_count; i++) {
v = buckets[i];
insertionSort();//调用插入排序,代码见插入排序代码。
for (j = 0; j < v.size(); j++) {
result.push_back(v[j]);
}
}
v = result;
len = v.size();
}
Java
//桶排序
public void bucketSort() {
int i, j, maxNum = Collections.max(v), minNum = Collections.min(v);
int bucketSize = 5; //桶容量
int bucketCount = ((maxNum - minNum) / bucketSize) + 1;
Vector<Integer> result = new Vector<>();
Vector<Vector<Integer>> buckets = new Vector<Vector<Integer>>();
for (i = 0; i < bucketCount; i++){
buckets.add(new Vector<>());
}
for (i = 0; i < v.size(); i++) {
buckets.get((v.get(i) - minNum) / bucketSize).add(v.get(i));
}
for (i = 0; i < bucketCount; i++) {
v = buckets.get(i);
insertionSort();
for (j = 0; j < v.size(); j++) {
result.add(v.get(j));
}
}
v = result;
len = v.size();
}
算法分析
桶排序最好情况下使用线性时间O(n),桶排序的时间复杂度,取决与对各个桶之间数据进行排序的时间复杂度,因为其它部分的时间复杂度都为O(n)。很显然,桶划分的越小,各个桶之间的数据越少,排序所用的时间也会越少。但相应的空间消耗就会增大。
基数排序(Radix Sort)
基数排序思路是根据分别根据一个数的每位数(个、十、百...)大小,从低位到高位进行排序,每次排序能保证:如果此位是某几个数的最高位,那么排序结束后队列中这几个数相对位置则是已排序状态。
算法思路
- 得到数组中最大数的位数:maxDigit;
- 循环maxDigit次,从最低位开始对原始数组进行计数排序(因为排序范围只有0~9);
图解

代码
C++
//基数排序
void radixSort() {
int mod = 10, dev = 1, bit_num, max_digit;
int i, j, k;
vector <int>* buckets;
max_digit = log10(*max_element(v.begin(), v.end())) + 1; //求容器中最大数的位数
for (i = 0; i < max_digit; i++, dev *= 10, mod *= 10) {
buckets = new vector<int>[10];
for (j = 0; j < v.size(); j++) {
bit_num = v[j] % mod / dev;
buckets[bit_num].push_back(v[j]);
}
v.clear();
for (j = 0; j < 10; j++) {
for (k = 0; k < buckets[j].size(); k++) {
v.push_back(buckets[j][k]);
}
}
}
len = v.size();
}
Java
//基数排序
public void radixSort() {
int mod = 10, dev = 1,bitNum, maxDigit;
int i, j;
Vector<Vector<Integer>> buckets;
maxDigit = String.valueOf(Collections.max(v)).length(); //获取数组v最最大数的位数
for (i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
buckets = new Vector<Vector<Integer>>();
buckets.setSize(10);
for (j = 0; j < v.size(); j++) {
bitNum = v.get(j) % mod / dev;
if (buckets.get(bitNum) == null) {
buckets.set(bitNum, new Vector<>());
}
buckets.get(bitNum).add(v.get(j));
}
v.clear();
for (j = 0; j < buckets.size(); j++) {
if (buckets.get(j) != null) {
while (buckets.get(j).size() != 0){
v.add(buckets.get(j).firstElement());
buckets.get(j).remove(0);
}
}
}
}
len = v.size();
}
算法分析
基数排序基于分别排序,分别收集,所以是稳定的。但基数排序的性能比桶排序要略差,每位数的桶分配都需要O(n)的时间复杂度,而分配之后得到的新序列又需要O(n)的时间复杂度。假如待排数据的最大数的位数(max_digit)为d,则基数排序的时间复杂度将是O(d*2n) ,当然d要远远小于n,因此基本上还是线性级别的。
基数排序的空间复杂度为O(n+k),其中k为桶的数量。一般来说n>>k,因此额外空间需要大概n个左右。
源代码下载
链接:https://pan.baidu.com/s/1hUbSsRV8rZUEYleyHF0UFQ
提取码:Yuri

