SkipList原理与实现

合集 - 数据结构与算法(2)
1.SkipList原理与实现
2.二叉堆原理与实现
收起

机制

链表中查询的效率的复杂度是O(n), 有没有办法提升这个查询复杂度呢? 最简单的想法就是在原始的链表上构建多层索引.
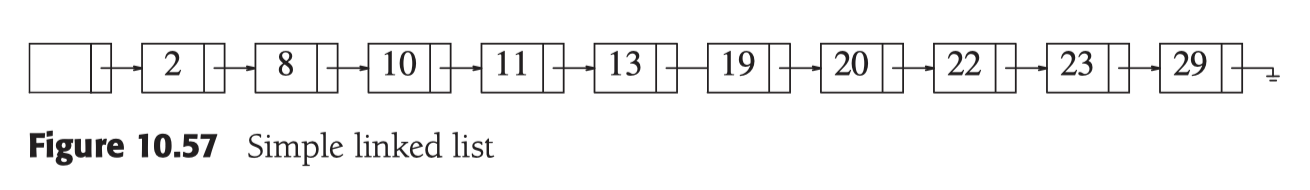
image.png

在level 1(最底层为0), 每2位插入一个索引, 查询复杂度便是 O(N/2 + 1)
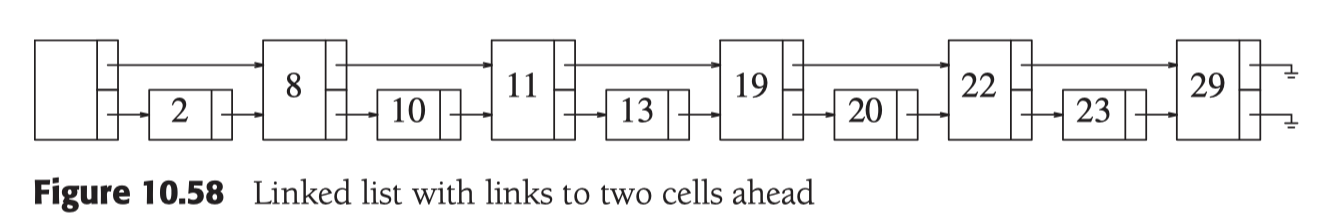
image.png

在level 2, 每四位插入一个索引, 查询复杂度便是 O(N/4 + 2)
image.png

那么推广开来, 如果我们有这样的一组链表, 在level i, 每间隔第 \(2^{i}\)元素就有一个链接
image.png
在level 1, 每一个节点之间有一个链接
在level 2, 每两个节点之间有一个链接
在level 3, 每四个节点之间有一个链接
在level 4, 每八个节点之间有一个链接.
这样我们可以看到, 每向上一层, 数据量就减少了 1/2, 所以查询的过程就近似变成了2分查找, **查询性能就变成了稳定的O(logN). **
索引的存储空间为\(Sn = n/2 + n/4 + n/8 + n/16 + ... + 8 + 4 + n/2^k\) 其中 \(k = log(n/2)\)

\(1/2 * Sn = n/4 + n/8 + n/16 + ... + 8 + 4 + n/2^{k+1}\)

两式相减得到 \(1/2 * Sn = n/2 - n/2^{k+1}\) 所以 \(Sn = n - n/2^k\)所以 \(Sn = n - 2\)
因此这样的数据结构总的空间复杂度为 2n - 2.

但是这样的数据结构存在一个问题, 严格要求每一层按照 \(2^{i}\)的间隔链接很难在持续插入的过程中维护.

当插入一个新元素的时候, 需要为他分配一个新的节点, 此时我们需要决定该节点是多少阶的. 通过观察 Figure 10.60 可以发现, 有1/2的元素是1阶的, 有 1/4 的元素是2阶的, 所以大约 \(1/2^i\)的节点是第 i 阶的.
那么根据这个性质, 我们就可以通过随机统计的方式来判断新元素应该插入的阶数. 最容易得做法就是抛一枚硬币直到正面出现并把抛硬币的总次数用作该节点的阶数.

连续抛i次才出现正面的概率是 \(1/2^i\), 而\(1/2^i\)**的节点是属于第 i 阶的. **

通常的计算阶数的方法

/**
 * 这个函数返回的是levelCount, 最小为1, 表示不构建索引.
 *
 * <p>
 * <li>1/2 概率返回1 表示不用构建索引
 * <li>1/2 概率返回2 表示构建一级索引
 * <li>1/4 概率返回3 表示构建二级索引
 * <li>1/8 概率返回4 表示构建三级索引
 *
 * @return
 */
private int randomLevel() {
    int level = 1;
    while (Math.random() < SKIPLIST_P && level < MAX_LEVEL) {
        level++;
    }
    return level;
}

通常p取值为 1/2 或者 1/4 表示两层之间的数据分布概率, Math.random()随机返回一个0-1之间的数, 这个就是模拟不断抛硬币的过程, height 为累计的抛硬币的次数.

因此跳表的实现, 是利用了随机化算法来计算新插入节点的阶数, 而这个阶数的数学期望能保证每一层数据能随机化的递减 1/2, 通过这样来保证最终插入和查找复杂度的期望都为 O(logN).

相比于红黑树
优势

  1. 插入 查找 删除的复杂度和红黑树一样
  2. 区间查找的效率更高
  3. 代码实现更简单
  4. 并且可以通过插入节点阶数生成的策略来平衡时间和空间复杂度的不同需求. 比如我们可以让每一层的数据为下一层的1/3. 这种情况下索引存储量 为 n/3 + n/9 + n/27 + ... 2 = n / 2 空间占用就缩小一半.

劣势

  1. 跳表的内存占用相比会大一点, 不过因为索引其实可以只存储key和指针, 实际的空间开销往往没有那么大

实现

定义数据结构

public class Node {
    public int value = -1;
    private Node forwards[] = new Node[MAX_LEVEL];
}

每一个元素表示为一个Node, Node 的level由上面提到的随机函数决定. Level i 的 node 有 i 个 forward 指针. 这里会比较费空间, 因为即使是 level 1, forwards数组的空间也分配了. 感觉这不是一个很好的做法, 欢迎读者给我指点下

查找

image.png
从最高层查找到最底层, 如果下一个Node的value比搜索值小, 那么在同层向后继续搜索. 如果下一个Node为空或下一个Node的value大于搜索值, 则跳转到下一层.
最后会走到最下层 level1, 和 搜索值进行比较.
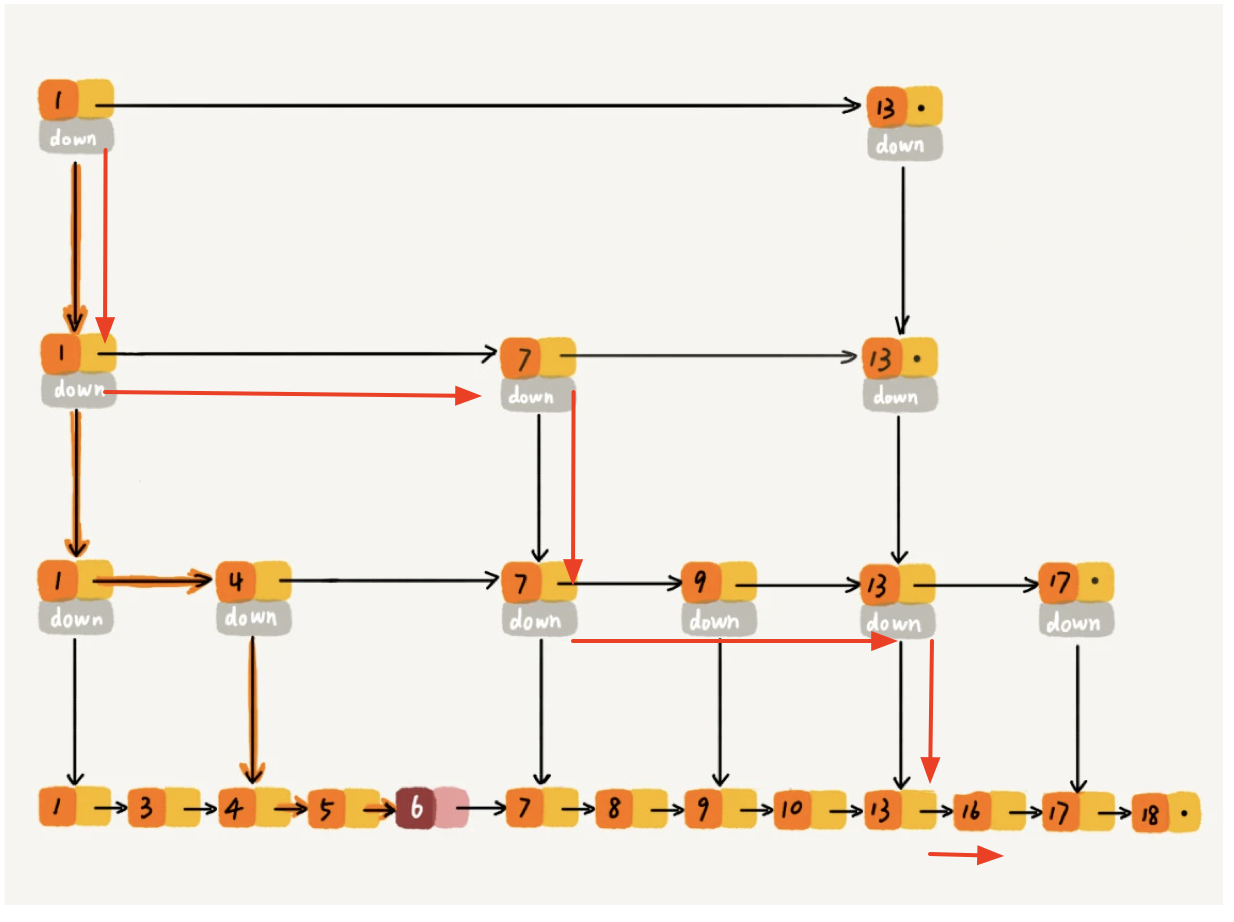
image.png
样例实现

public Node find(int value) {
    Node p = head;
    for (int i = levelCount - 1; i >= 0; i--) {
        // 先同层查找, 直到出现 value > target. 出现后 level + 1
        while (p.forwards[i] != null && p.forwards[i].value < value) {
            p = p.forwards[i];
        }
    }
 
    // 最后会跳转到level 1
    if (p.forwards[0] != null && p.forwards[0].value == value) {
        return p.forwards[0];
    } else {
        return null;
    }
}

插入

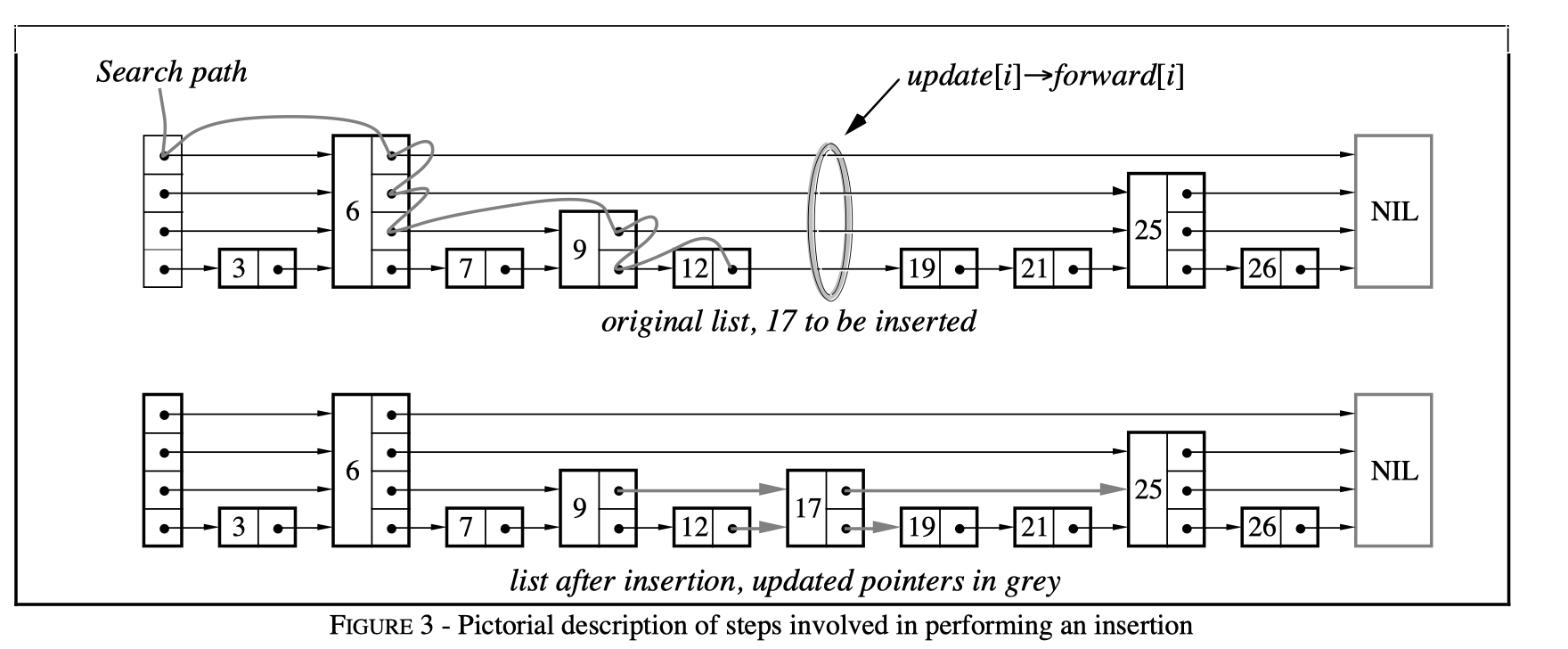
image.pngimage.png

  1. 从最大level到最小level遍历搜索, 和前面的搜索过程类似, 只不过在每次转折向下的时候记录该level的Node(这个就是要插入位置的前置level)
  2. 如果在最低层找到了这个searchKey, 则更新该value, 这个有点类似于map的语义
  3. 如果没有则通过randomLevel 生成随机高度
  4. 如果level比当前高度高, 那么将高出那部分的updates[i] 指向 head节点
  5. 插入新value update[i] -> newNode -> update[i].old_forward

样例实现
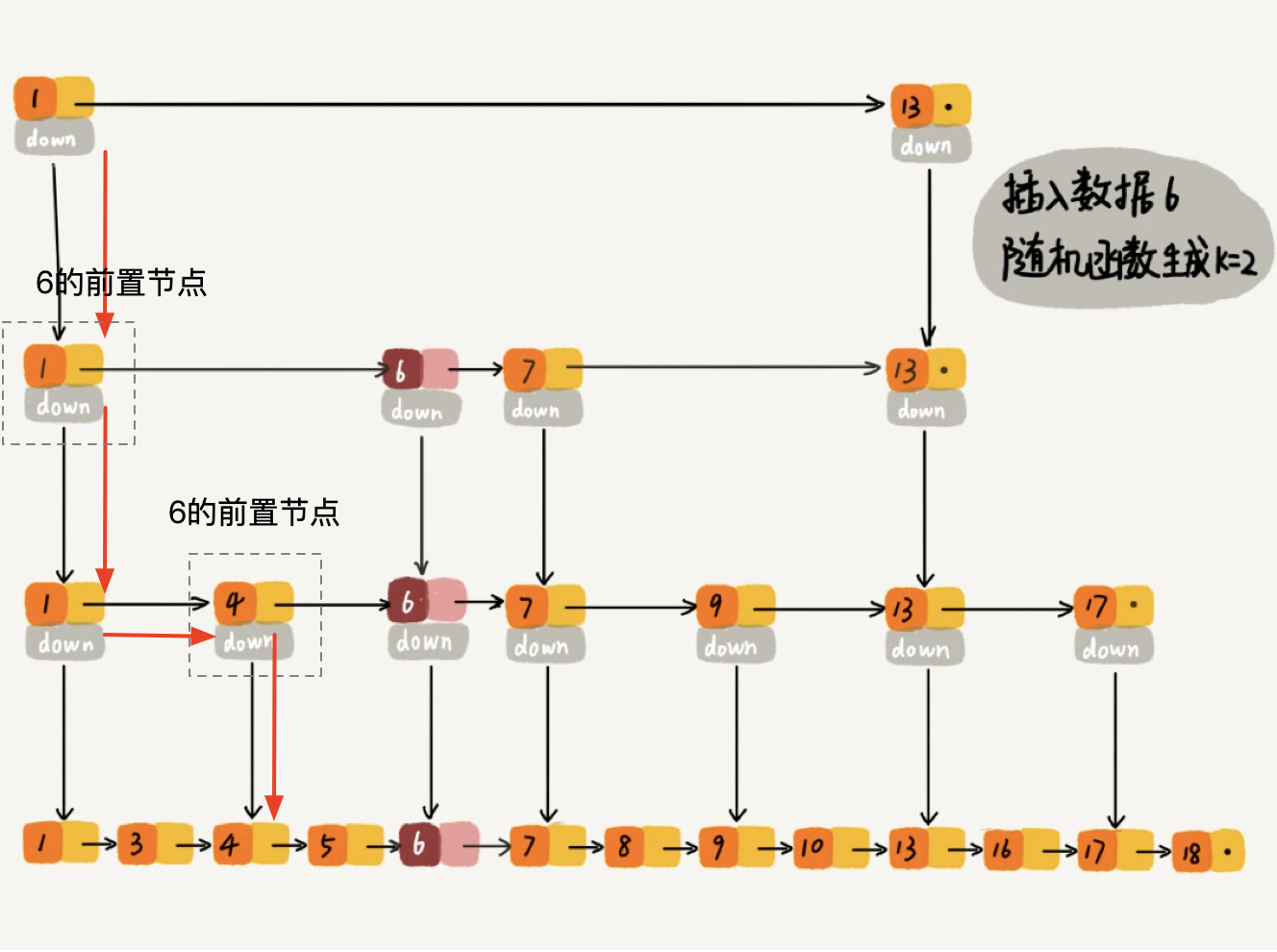
image.png

public void insert(int value) {
    int level = randomLevel();
 
    Node newNode = new Node();
    newNode.value = value;
    Node[] updates = new Node[level];
    for (int i = 0; i < level; i++) {
        updates[i] = head;
    }
 
    Node p = head;
    for (int i = level - 1; i >= 0; i--) {
        while (p.forwards[i] != null && p.forwards[i].value < value) {
            p = p.forwards[i];
        }
        // 向前一直查找直到找到 末节点或者p.value > value
        // updates 存储的要保存的前置节点
        updates[i] = p;
    }
    for (int i = 0; i < level; i++) {
        newNode.forwards[i] = updates[i].forwards[i];
        updates[i].forwards[i] = newNode;
    }
 
    if (level > this.levelCount) {
        this.levelCount = level;
    }
}

删除

image.png

  1. 删除过程同样也是先搜索, 并找到前置节点
  2. 如果最后一层遇到有相同key, 那么遍历各层将前置节点的指向更新
  3. 最后检查head Node的最高层如果指向为空则降低当前level.
public void delete(int value) {
    Node p = head;
    Node[] updates = new Node[levelCount];
    // 找到前置节点
    for (int i = levelCount - 1; i >= 0; i--) {
        while (p.forwards[i] != null && p.forwards[i].value < value) {
            p = p.forwards[i];
        }
        updates[i] = p;
    }
 
    if (p.forwards[0] != null && p.forwards[0].value == value) {
        for (int i = levelCount - 1; i >= 0; i--) {
            if (updates[i].forwards[i] != null && updates[i].forwards[i].value == value) {
                updates[i].forwards[i] = updates[i].forwards[i].forwards[i];
            }
        }
    }
 
    // head 指向为空的节点都剔除.
    while (levelCount > 1 && head.forwards[levelCount] == null) {
        levelCount--;
    }
}

第二种实现 不记录updates的方法, 在循环的过程中就执行删除

public void delete2(int value) {
    Node p = head;
    // 找到前置节点
    for (int i = levelCount - 1; i >= 0; i--) {
        while (p.forwards[i] != null && p.forwards[i].value < value) {
            p = p.forwards[i];
        }
        if (p.forwards[i] != null && p.forwards[i].value == value) {
            p.forwards[i] = p.forwards[i].forwards[i];
        }
    }
 
    // head 指向为空的节点都剔除.
    while (levelCount > 1 && head.forwards[levelCount] == null) {
        levelCount--;
    }
}

打印

在实现的过程中期望能打印skiplist的结构来检测插入和删除的准确性. print的难点在于怎么去实现每一层的数据对齐.
大致思路是

(1) 首先计算最底层 每一个Node 到第一位的位次
例如以下样例中

level 1:                                  10               111      300
level 0:        1        2        4       10       80      111      300     1213

1 的位次为1, 2的位次为2, 4的位次为3

(2) 通过String.format("% 8d", p.value)保证每个value打印的宽度对齐

(3) 通过计算上面每一层的Node和本层距离第一位的差值补齐空格

public void print() {
    List<String> strings = new ArrayList<>(levelCount);
 
    // 最底层每个Node和第一个node的delta
    Map<Node, Integer> bottomNode2Delta = new HashMap<>();
    Node p = head.forwards[0];
    int delta = 0;
    StringBuilder builder = new StringBuilder();
    while (p.forwards[0] != null) {
        bottomNode2Delta.put(p, ++delta);
        builder.append(String.format("% 8d", p.value));
        builder.append(" ");
        p = p.forwards[0];
    }
    bottomNode2Delta.put(p, ++delta);
    builder.append(String.format("% 8d", p.value));
    strings.add(builder.toString());
 
    if (levelCount > 1) {
        for (int i = 1; i <= levelCount - 1; i++) {
            p = head.forwards[i];
            builder = new StringBuilder();
            int count = 0;
            while (p.forwards[i] != null) {
                // 相差的数字个数
                int number = (bottomNode2Delta.get(p) - ++count);
                // 空格 + 数字本身间隔设置为8
                int blank = number + number * 8;
                for (int j = 0; j < blank; j++) {
                    builder.append(" ");
                }
                // 补齐之后count 对齐
                count = bottomNode2Delta.get(p);
                builder.append(String.format("% 8d", p.value));
                builder.append(" ");
                p = p.forwards[i];
            }
            int number = (bottomNode2Delta.get(p) - ++count);
            int blank = number + number * 8;
            for (int j = 0; j < blank; j++) {
                builder.append(" ");
            }
 
            builder.append(String.format("% 8d", p.value));
            strings.add(builder.toString());
        }
    }
 
    for (int i = strings.size() - 1; i >= 0; i--) {
        System.out.printf("level% 2d: %s%n", i, strings.get(i));
    }
}

效果

    public static void main(String[] args) {
        SkipList skipList = new SkipList();
        skipList.insert(2);
 
        skipList.insert(1);
        skipList.insert(4);
        skipList.insert(300);
        skipList.insert(80);
        skipList.insert(10);
        skipList.insert(111);
        skipList.insert(1213);
        skipList.insert(32);
 
        skipList.print();
 
        skipList.delete2(32);
 
        System.out.println("after delete");
 
        skipList.print();
    }
 
level 2:                                                            111
level 1:                                  10                        111      300
level 0:        1        2        4       10       32       80      111      300     1213
after delete
level 1:                                  10               111      300
level 0:        1        2        4       10       80      111      300     1213

这样就非常的直观可以看到跳表的结构

工业实现

redis的sorted set
hbase中LSM Tree的内存的有序集合
java ConcurrentSkipListSet ConcurrentSkipListMap

参考

Skip Lists: A Probabilistic Alternative to Balanced Trees
<数据结构与算法分析 Java描述> 10.4.2
<HBase原理与实践> 2.1 跳跃表
王争数据结构与算法之美#17
Skip List--跳表（全网最详细的跳表文章没有之一）
https://zhuanlan.zhihu.com/p/33674267

posted @   Aitozi  阅读(206)  评论(0)  编辑  收藏  举报
相关博文：
· 二叉堆原理与实现
· Paimon的写入流程
· 跳表的设计与实现
· 【数据结构】跳表(SkipList)
· 数据结构之跳表SkipList、ConcurrentSkipListMap
阅读排行：
· 被坑几百块钱后，我竟然真的恢复了删除的微信聊天记录！
· 没有Manus邀请码？试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单，K8s 太复杂？w7panel 让容器管理更轻松！
点击右上角即可分享
微信分享提示