博客作业04--树
1.学习总结
1.1树结构思维导图
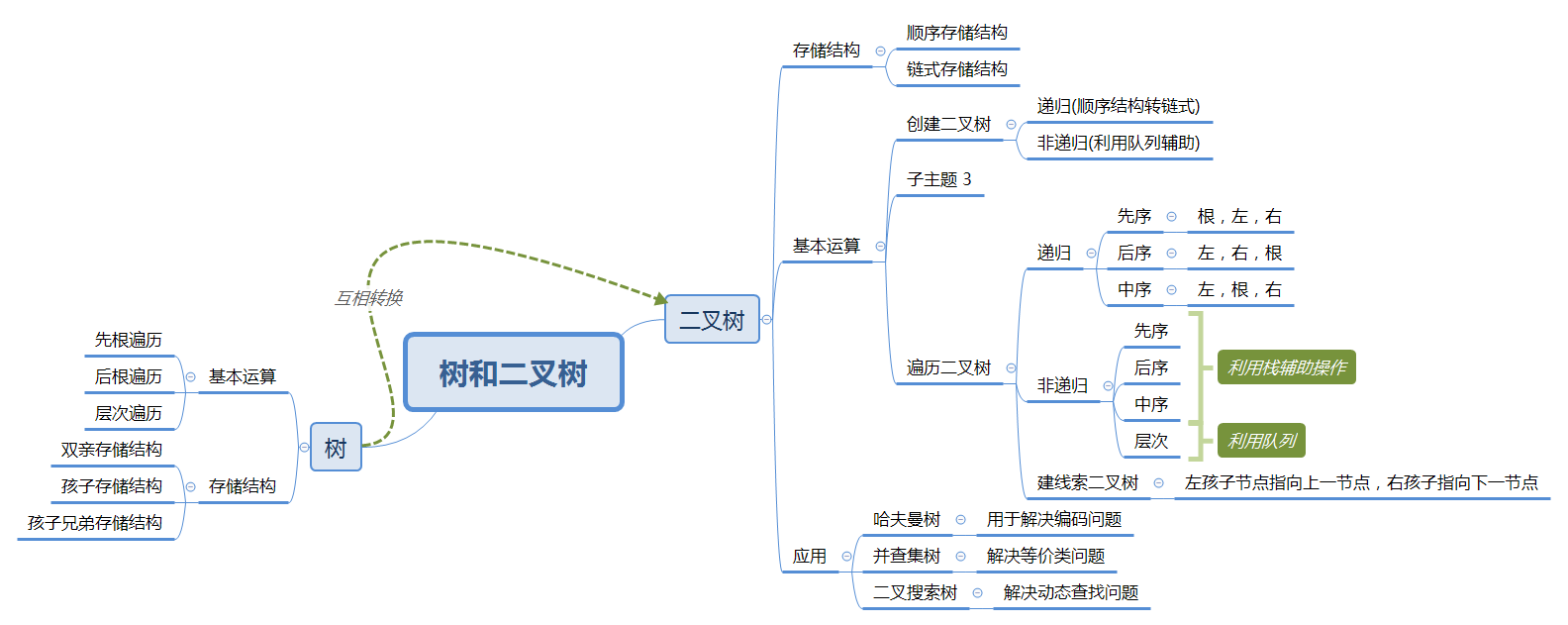
1.2 树结构学习体会
树这一章比前面的线性结构难,特别是其中递归的运用,让人觉得难以理解,而且树的应用也很多,所以要学好这一章要花更多时间
2.PTA实验作业
题目1:6-4 jmu-ds-表达式树
设计思路
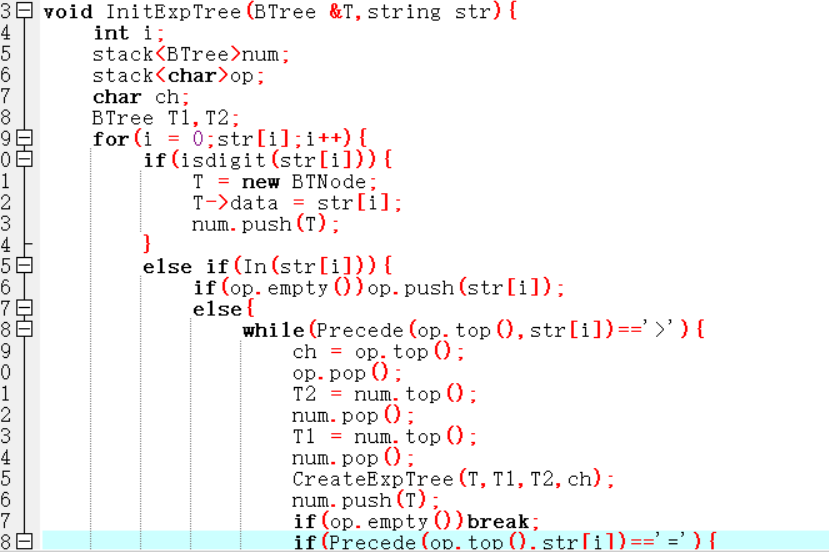
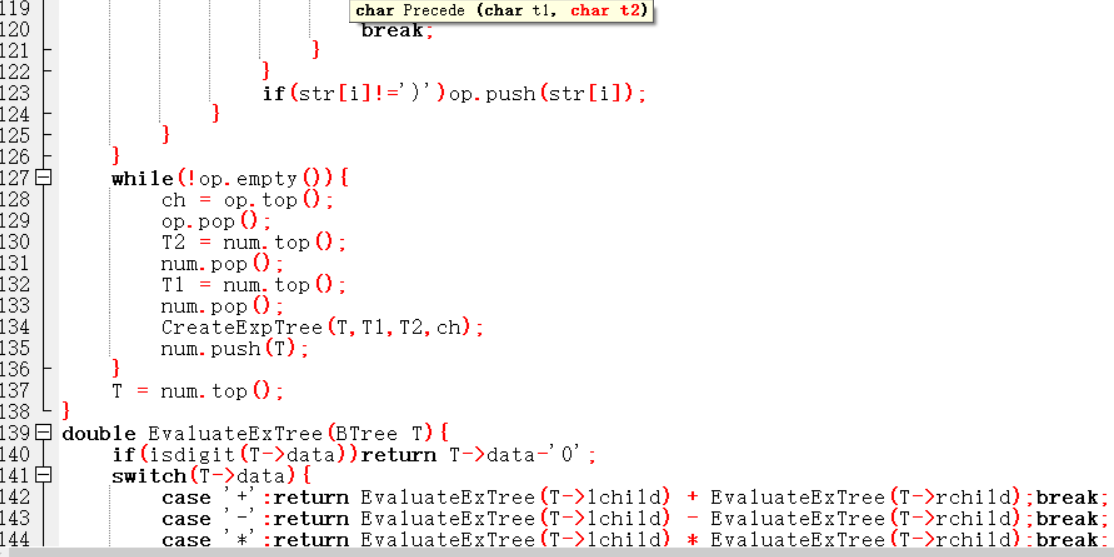
void InitExpTree(BTree &T,string str):
定义一个树栈和符号栈
for i = 1 to 字符串结束
如果str[i]是数字
建树存入树栈
如果str[i]是字符
如果栈为空,则直接存入符号栈
否则比较优先级
当栈内优先级和str[i]较高,符号出栈和树栈内两个数字建树
当栈内优先级和str[i]相等,这种情况是左括号遇到右括号直接出栈
否则符号入字符栈
end for
符号栈全部出栈建树并存入树栈
T = 树栈.top()
double EvaluateExTree(BTree T):
如果 T->data 为数字 转换成数字
如果 T->data 为符号,就递归调用该函数来计算要注意0不能为除数
代码截图
PTA提交列表说明

我觉得这题挺难的,只得5分的那次是因为判断优先级的函数理解的不够清楚
之后15分是由于没有考虑括号的情况,让右括号也入栈,弄了很久,最后看了同
学的代码才会做
题目2:7-3 jmu-ds-二叉树层次遍历
设计思路
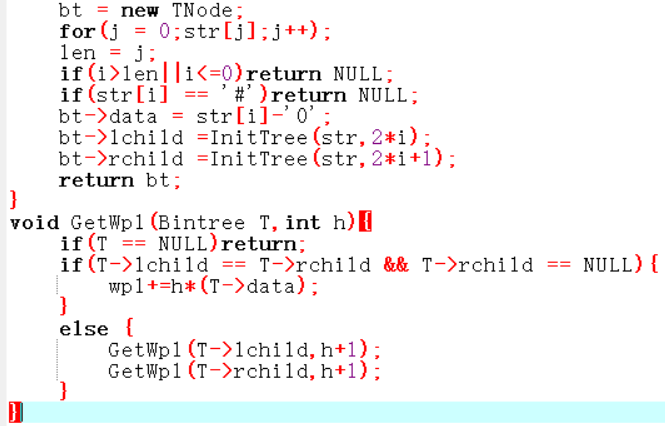
递归法建二叉树:
len = str长度
如果i不合法或str[i] = #,返回NULL
bt->data = str[i]
分别创建左右子树
返回bt;
GetWpl(Bintree T,int h):
如果 T = NULL 返回NULL
如果T左右子树都空,wpl+=T->data*h
否则 GetWpl(T->lchild)GetWpl(T->rchild)
代码截图

PTA提交列表说明

这题主要是一开始建树时使用了层次遍历法,代码量较大,还不能正确,改了递归法后就好了
题目3:7-2 根据后序和中序遍历输出先序遍历
设计思路
Bintree InitBintree(int * in,int * post,int length):
如果length 为0返回NULL
否则T->data = 中序遍历最后一位
forroot = 0 to root>=length
找到后序遍历最后一位在中序遍历的位置
递归建立左右子树:
T->lchild = InitBintree(in,post,root);
T->rchild = InitBintree(in + root+1,post+root,length - root - 1)
返回T
void Postorder(Bintree T):
递归出口:T == NULL
输出T->data
Postorder(左子树)
Postorder(右子树)
代码截图

PTA提交列表说明

没什么问题
3.截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的得分:199
4. 阅读代码
问题:求反转二叉树
#include <stdio.h>
#include <stdlib.h>
typedef struct Tree {
int val;
struct Tree* left;
struct Tree* right;
}Tree;
void CreateBiTree(Tree**T)
{
int val;
scanf("%d", &val);
if(val == -1)
*T = NULL;
else
{
*T = (Tree *)malloc(sizeof(Tree));
(*T)->val = val;
CreateBiTree(&(*T)->left);
CreateBiTree(&(*T)->right);
}
}
void ExchangeLeftRight(Tree **root)
{
Tree * node = (*root)->right;
(*root)->right = (*root)->left;
(*root)->left = node;
}
void RecursiveReversal(Tree *root) //反转二叉树
{
if (root != NULL)
{
ExchangeLeftRight(&root);
RecursiveReversal(root->left);
RecursiveReversal(root->right);
}
}
void Print(Tree*root)
{
if (root != NULL)
{
Print(root->left);
printf("%d ", root->val);
Print(root->right);
}
}
int main()
{
Tree* root;
CreateBiTree(&root);
Print(root);
printf("\n");
RecursiveReversal(root);
Print(root);
return 0;
}
这一题主要用到的是递归的算法,只要把左右子树调换,并不是很难,但是我对递归的方法理解的不够好,这一题用递归大大简化了代码,确实不错
5. 代码Git提交记录截图




