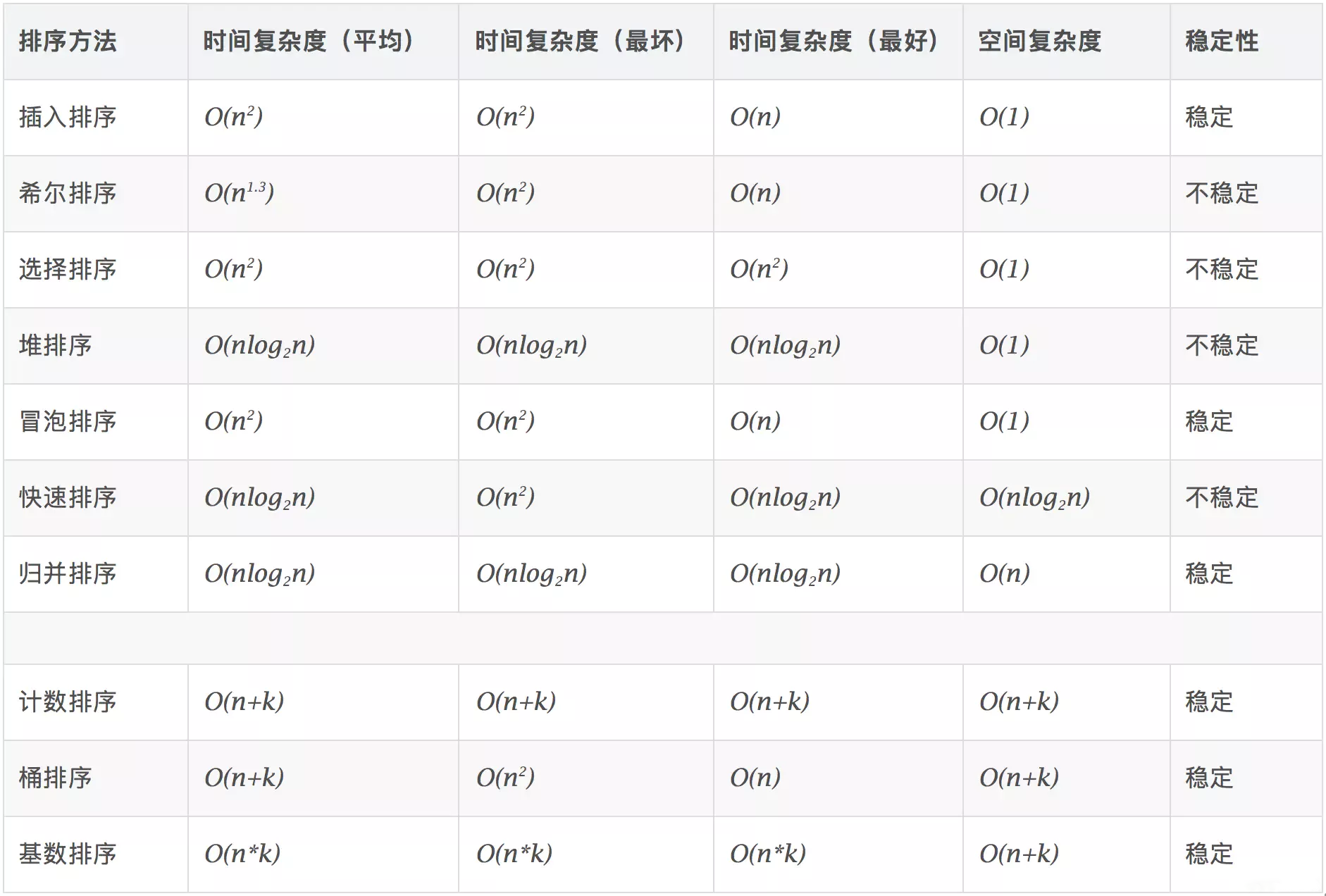
十大排序
(平均/最好/最坏)时间复杂度、空间复杂度、稳定性
注意:main方法测试调用统一提取出来,按照需求自己打开/关闭注释去调用
public static void main(String[] args) {
//随机数个数
int number = 1000;
//随机数最大值
int maxNum = 1000;
//随机数最小值
int minNum = 1;
Random random = new Random();
Integer[] arr = new Integer[number];
for (int i = 0; i < number; i++) {
arr[i] = random.nextInt(maxNum - minNum) + minNum;
}
//输出排序前的样子
System.out.println(Arrays.toString(arr));
long startTime = System.currentTimeMillis();
//调用排序方法,主函数的其他代码无关紧要,主要是为了生成数据,打印结果
BubbleSort.bubbleSort(arr);
//SelectSort.selectSort(arr);
//InsertSort.insertSort(arr);
//ShellSort.shellSort(arr);
//QuickSort.quickSort(arr);
//MergeSort.mergeSort(arr);
long endTIme = System.currentTimeMillis();
//输出排序后的样子
System.out.println(Arrays.toString(arr));
//输出排序用时,生成数据时间不算,结果保留两位小数
System.out.println((endTIme - startTime) / 1000.0 + "秒");
}
注意:以下实现方法不唯一,只是给出相对于好的实现方式。
一、冒泡排序(Bubble Sort)
解释:前一个和后一个相比,如果前一个大于后一个,那么他们互换,每次循环找出一个最大的。
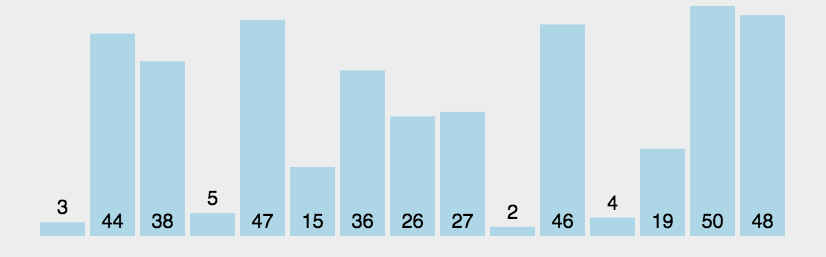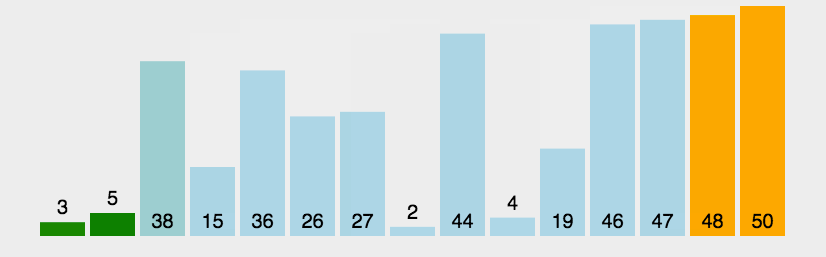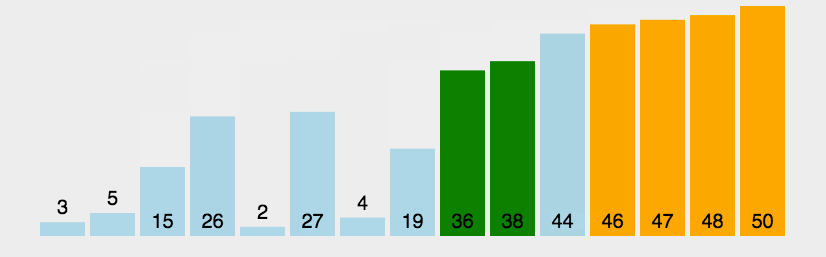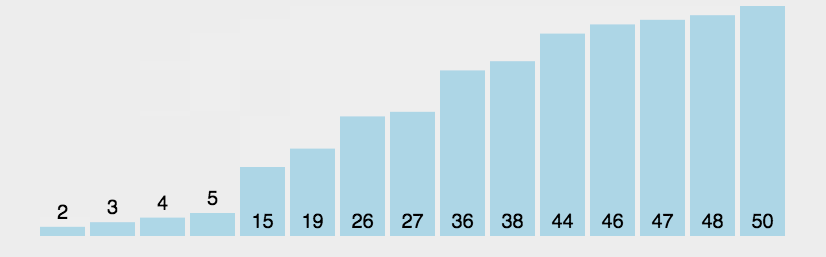
//冒泡排序
public class BubbleSort {
public static void bubbleSort(Integer[] arr) {
Integer t;
//例:arr.length=5,那么要执行4 3 2 1,总共四次
for (int i = arr.length - 1; i > 0; i--) {
/**
* 这个的作用就是说如果在一轮比较中没有发生对换的情况,
* 那么代表数组在这个时刻已经是有序的了,所以直接退出比较
*/
boolean flag = true;
//第一次应该循环0~4,第二次就循环0~3,以此类推
for (int j = 0; j < i; j++) {
//如果前一个大于后一个,那么他们对换
if (arr[j] > arr[j + 1]) {
t = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = t;
flag = false;
}
}
if (flag) {
break;
}
}
}
}
二、选择排序(Select Sort)
解释:每次循环中找到一个最小的,记录它的下标,然后对调。
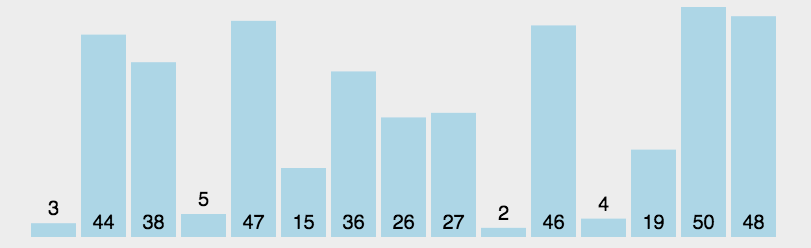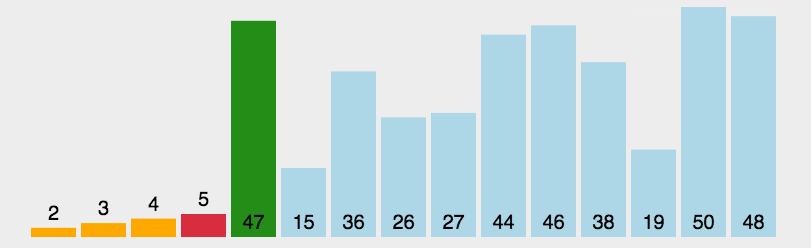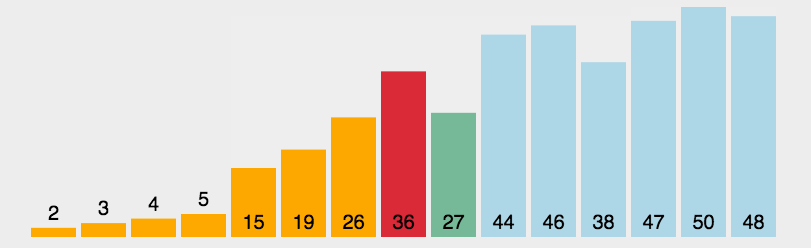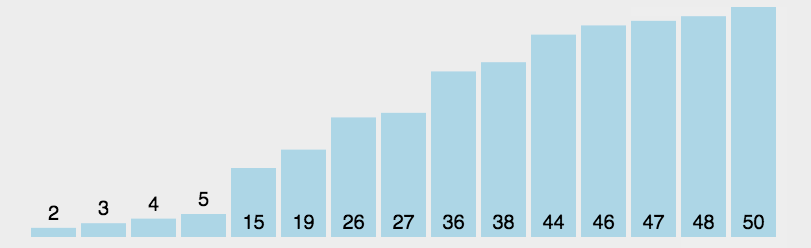
//选择排序
public class SelectSort {
public static void selectSort(Integer[] arr) {
Integer t;
for (int i = 0; i < arr.length - 1; i++) {
//把当前数组中的第i个当做最小的
int index = i;
for (int j = i + 1; j < arr.length; j++) {
//如果arr[j] < arr[index],记录更小的下标j
if (arr[j] < arr[index]) {
//在满足上面条件后,我们应该记录当前最小的下标
index = j;
}
}
//最后执行完本次循环后会得到arr中未完成排序部分最小的下标index,让他们交换
t = arr[i];
arr[i] = arr[index];
arr[index] = t;
}
}
}
三、插入排序(Insert Sort)
解释:将无序序列中的元素逐个插入到有序序列中,直到整个序列有序(一开始把第一个元素当做有序序列,其他后面元素是无序序列)
//插入排序
public class InsertSort {
public static void insertSort(Integer[] arr) {
Integer t;
for (int i = 0; i < arr.length - 1; i++) {
//拿出无序序列的第一个元素,去遍历整个有序序列进行比较
for (int j = i + 1; j > 0; j--) {
//如果arr[j]小于arr[j-1]他们对换
if (arr[j] < arr[j - 1]) {
t = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = t;
} else {
//当arr[j-1]小于arr[j]时,代表当前元素已经插入到有序序列的合适位置,退出当前循环进行下一个元素排序
break;
}
}
}
}
}
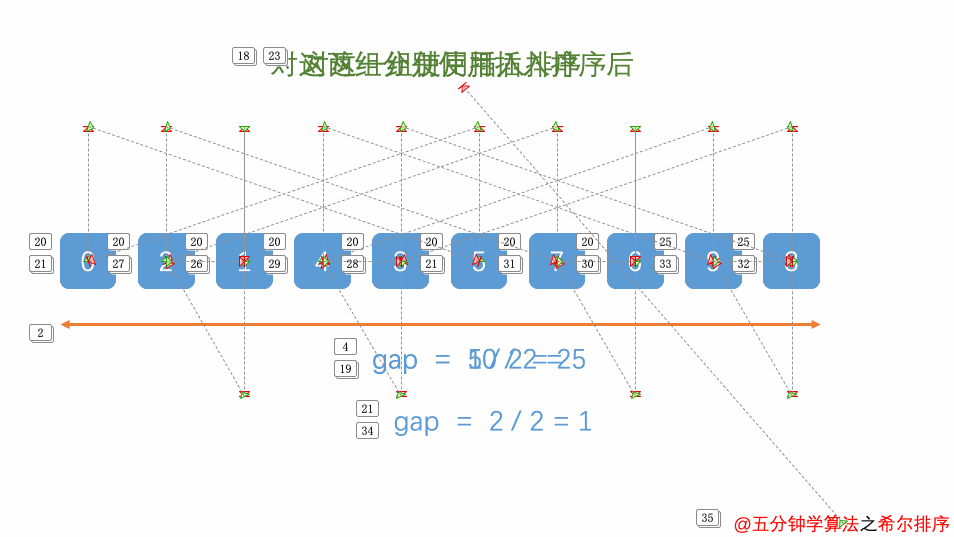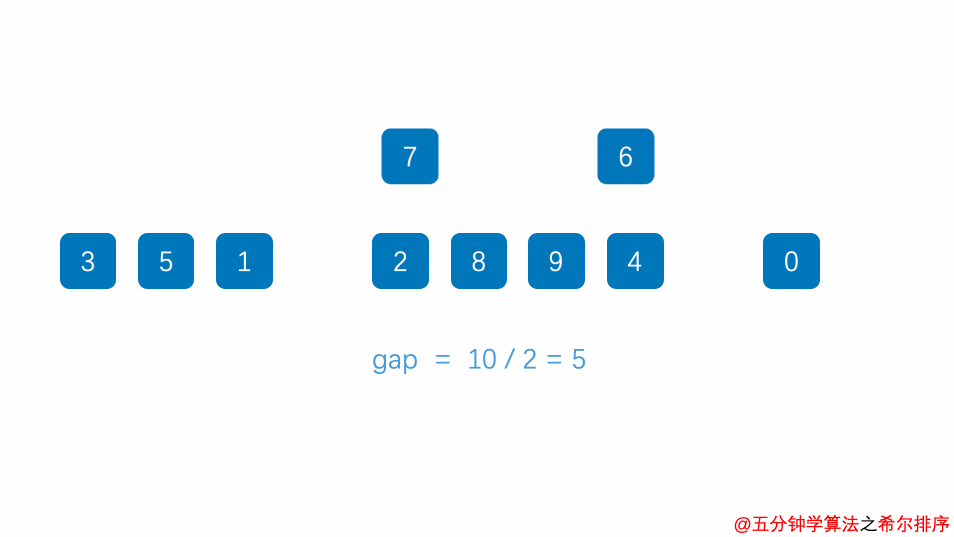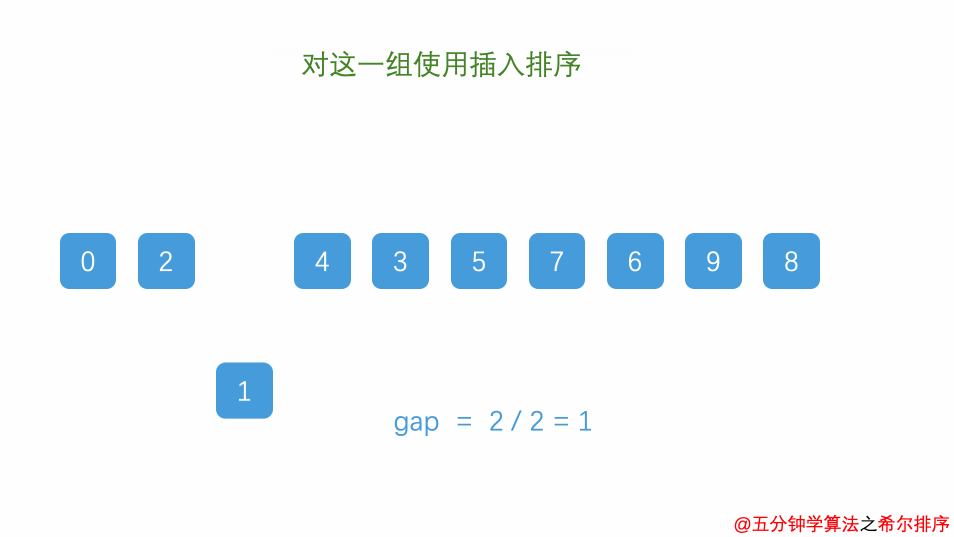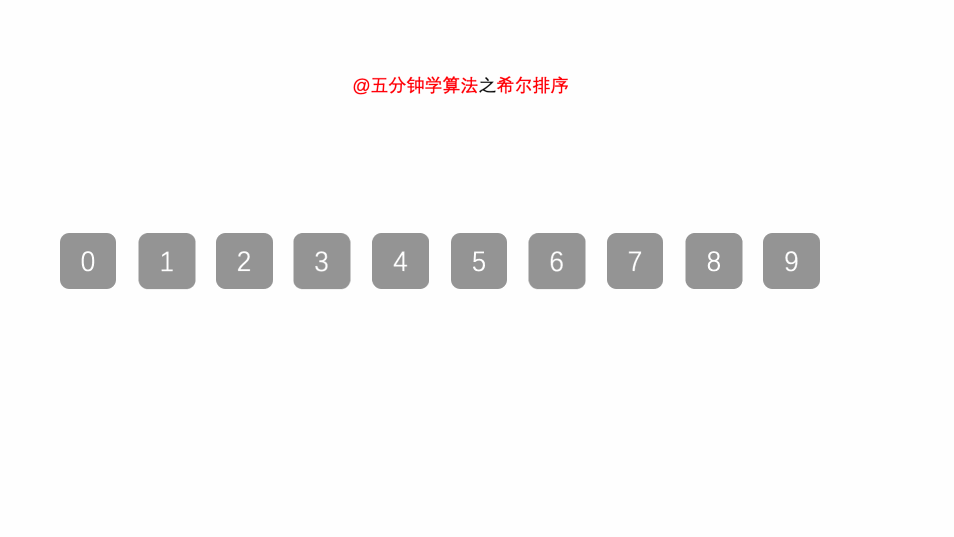
四、希尔排序(Shell Sort)
解释:基于插入排序的排序算法,通过比较一定间隔(增量)的元素来进行插入排序,不断缩小增量直至为1,最终完成排序。
//计算首次合适的一定间隔h的方法
int h=1;
while (h< arr.length/2){
h=2*h+1;
}
//例:arr的长度为10,那么一开始h等于7
//那按照h等于7的情况来看,希尔排序完成,它要走的间隔h分别为 7 3 1,因为每次执行一轮排序就会进行h=h/2
//希尔排序
public class ShellSort {
public static void shellSort(Integer[] arr) {
Integer t;
//计算首次合适的一定间隔h的
int h = 1;
while (h < arr.length / 2) {
h = 2 * h + 1;
}
while (h >= 1) {
/**这就是根据间隔h计算本次运行次数,不会就记代码吧
* 例arr.length=10,h=7是循环3次
* 例arr.length=10,h=3是循环7次
* 例arr.length=10,h=1是循环9次
*/
for (int i = 0; i < arr.length - h; i++) {
//这边要注意间隔是从arr后面往前取
for (int j = i + h; j >= h; j -= h) {
if (arr[j] < arr[j - h]) {
t = arr[j - h];
arr[j - h] = arr[j];
arr[j] = t;
} else {
break;
}
}
}
h = h / 2;
}
}
}
五、快速排序(Quick Sort)
解释:选取一个基准值(pivot),将序列分为小于和大于基准值的两部分,并对这两部分分别进行递归排序,最终完成排序。
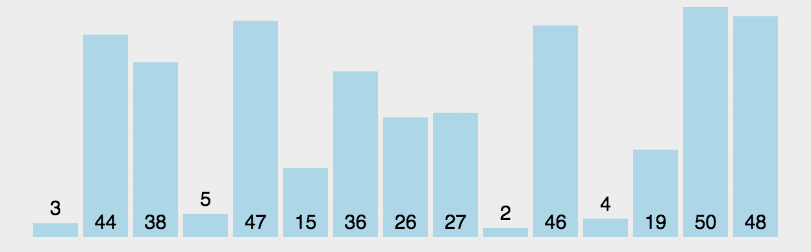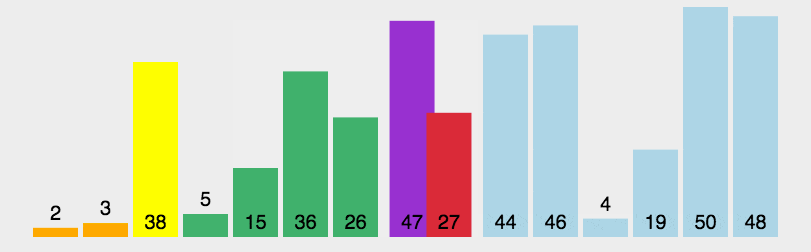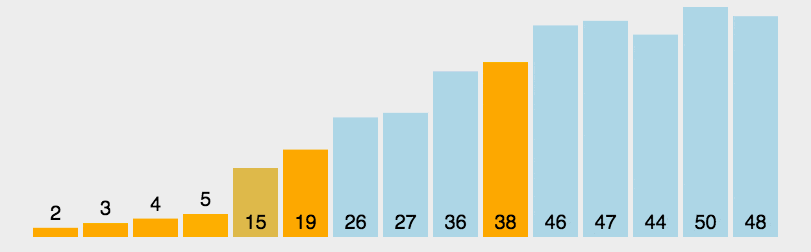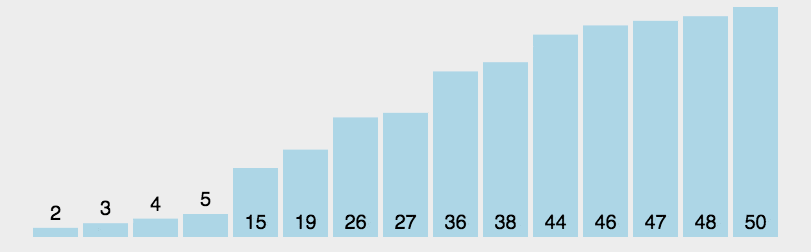
//快速排序,实现方法有很多,这是其中一种,但是原理是一样的
public class QuickSort {
public static void quickSort(Integer[] arr) {
//获取arr的左右下标,然后调用开始排序
int l = 0;
int r = arr.length - 1;
quickSort(arr, l, r);
}
public static void quickSort(Integer[] arr, int l, int r) {
if (l >= r) {
return;
}
//进行排序
int partition = partition(arr, l, r);
//左分区
quickSort(arr, l, partition - 1);
//又分区
quickSort(arr, partition + 1, r);
}
public static int partition(Integer[] arr, int l, int r) {
//记录基准下标,默认左边第一个
int leftBaseIndex = l;
Integer t;
while (l < r) {
//要先右边在左边,顺序不能错
//右边是找出大于arr[leftBaseIndex]的
while (l < r && arr[r] > arr[leftBaseIndex]) {
--r;
}
//左边是找出小于arr[leftBaseIndex]的
while (l < r && arr[l] <= arr[leftBaseIndex]) {
++l;
}
if (l < r) {
//交换
t = arr[l];
arr[l] = arr[r];
arr[r] = t;
}
}
t = arr[leftBaseIndex];
arr[leftBaseIndex] = arr[r];
arr[r] = t;
return r;
}
}
六、归并排序(Merge Sort)
解释:将序列不断划分为更小的子序列并对子序列进行排序,最后将子序列合并成一个有序序列,完成排序。
//获得中间位置
mid = l + (r - l) / 2
//归并排序
public class MergeSort {
public static void mergeSort(Integer[] arr) {
Integer[] assist = new Integer[arr.length];
int l = 0;
int r = arr.length - 1;
mergeSort(arr, l, r, assist);
}
public static void mergeSort(Integer[] arr, int l, int r, Integer[] assist) {
if (l >= r) {
return;
}
int mid = l + (r - l) / 2;
mergeSort(arr, l, mid, assist);
mergeSort(arr, mid + 1, r, assist);
merge(arr, l, mid, r, assist);
}
public static void merge(Integer[] arr, int l, int mid, int r, Integer[] assist) {
int i = l, p1 = l, p2 = mid + 1;
//把当前排序的左右两边的数据从小到大放到assist中
while (p1 <= mid && p2 <= r) {
if (arr[p1] < arr[p2]) {
assist[i++] = arr[p1++];
} else {
assist[i++] = arr[p2++];
}
}
//有可能是左边放完了,右边没放完
while (p1 <= mid) {
assist[i++] = arr[p1++];
}
//有可能是又边放完了,右边没放完
while (p2 <= r) {
assist[i++] = arr[p2++];
}
//将当前有序的数组返回arr
if (r + 1 - l >= 0) System.arraycopy(assist, l, arr, l, r + 1 - l);
}
}
注意:从这边开始,以下代码是偷来的,还没看,不知道有没有错,等有空再看再更新。。。。
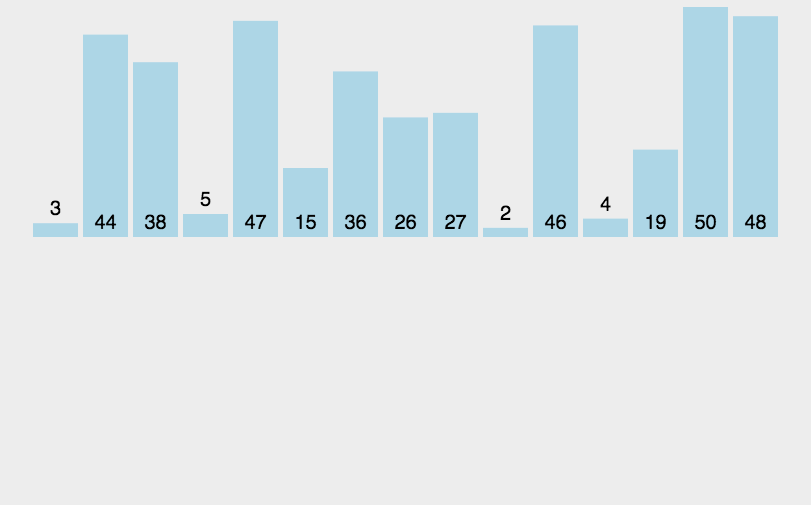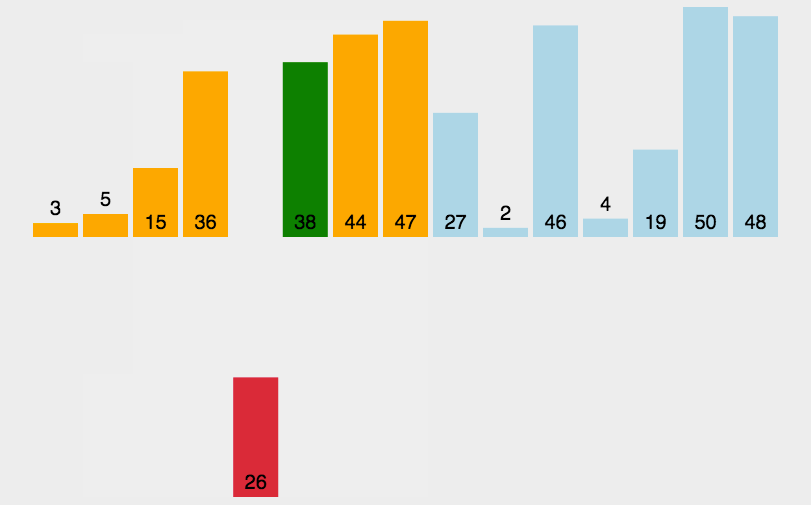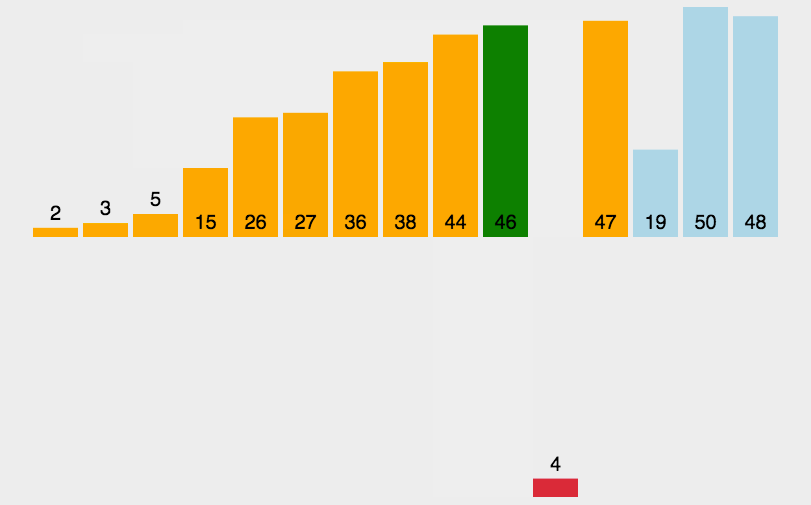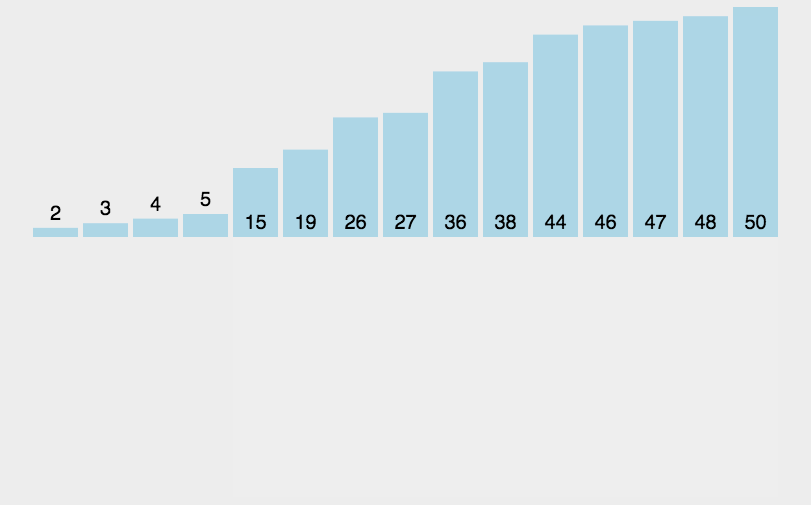
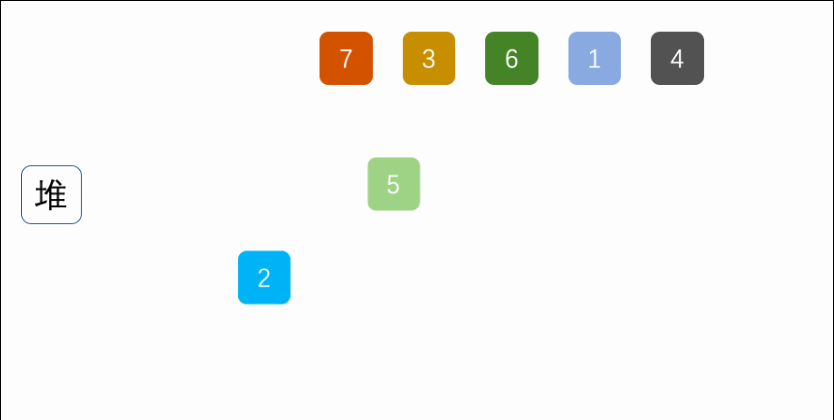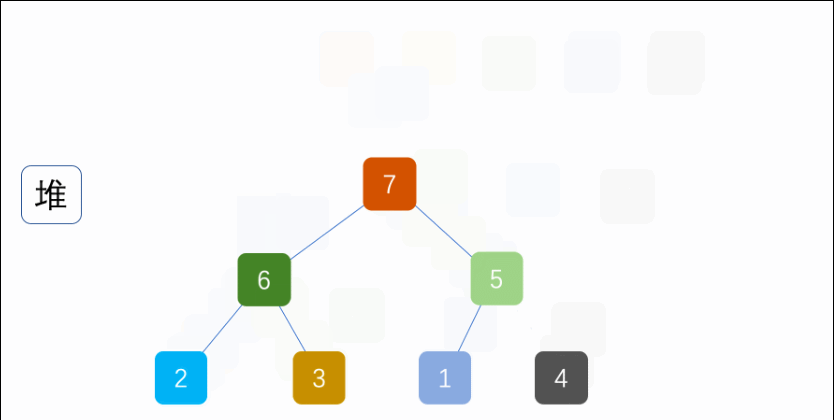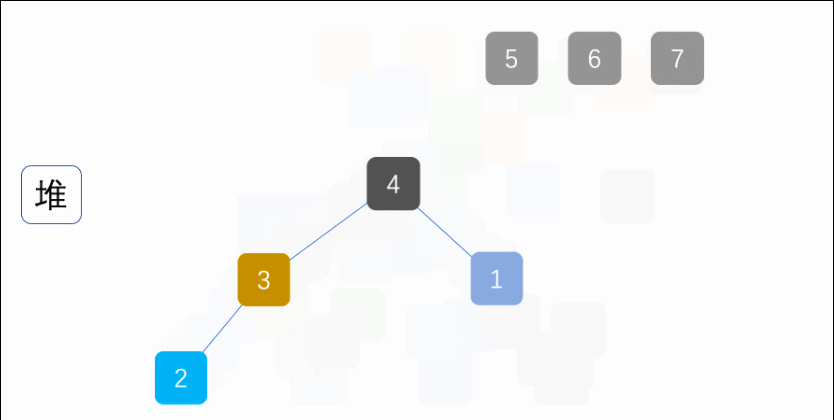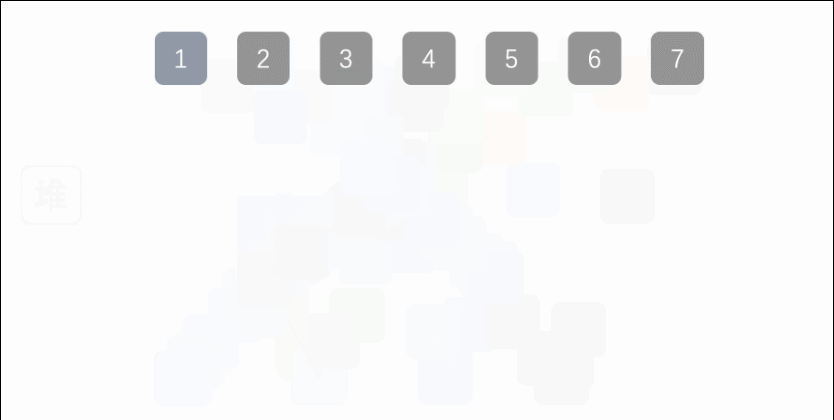
七、堆排序(Heap Sort)
解释:将待排序序列构建成最大堆或最小堆,不断将堆顶元素取出并调整堆结构,最终得到一个有序序列。
public class HeapSort {
public static void main(String[] args) {
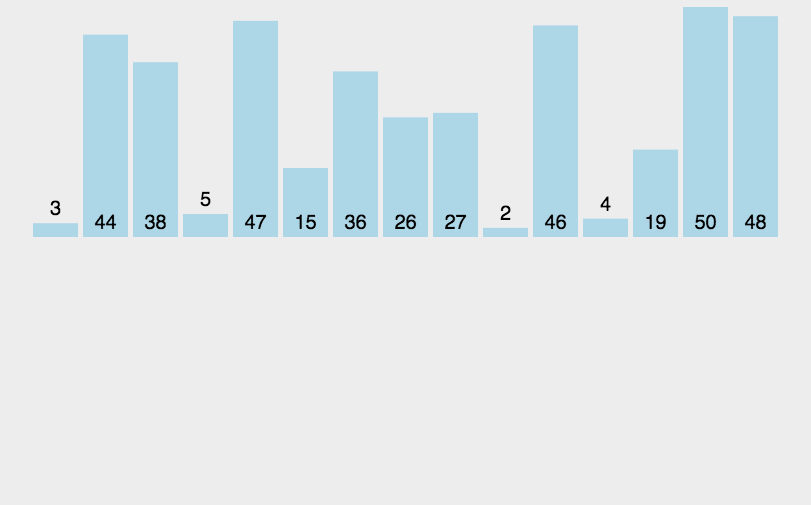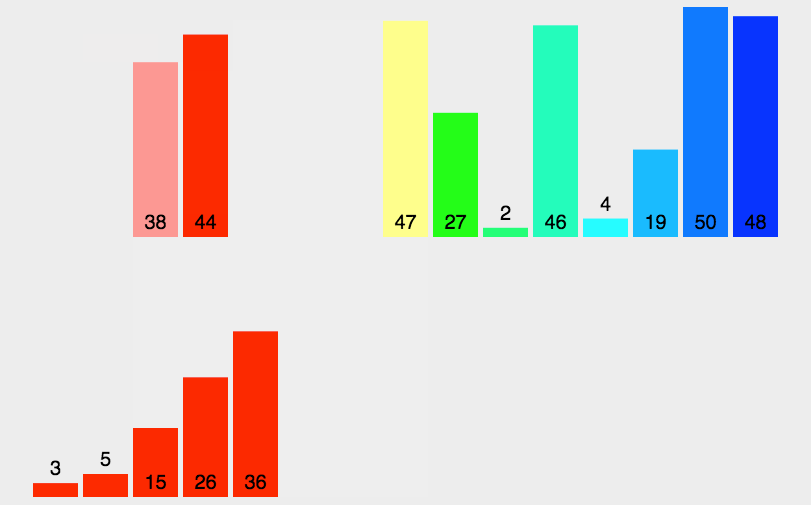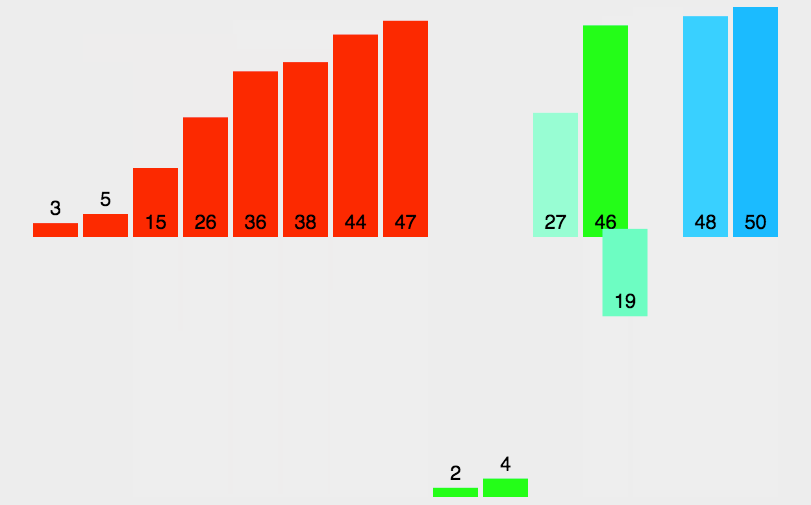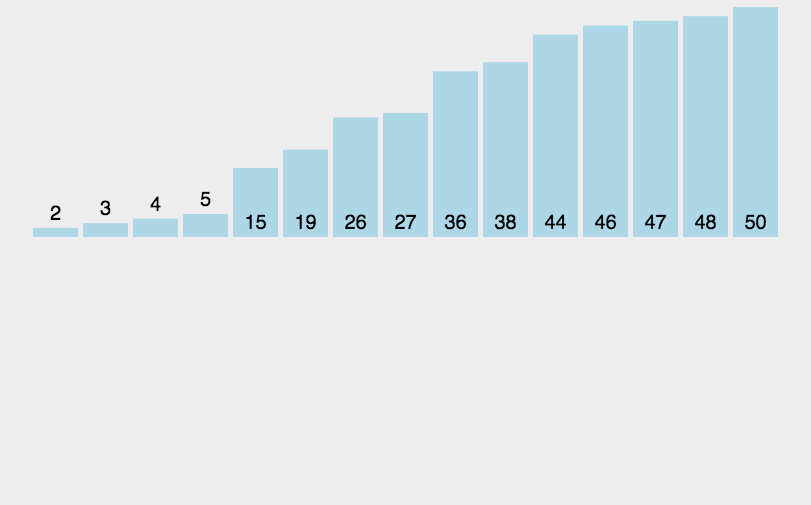
int a[]={3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
sort(a);
System.out.println(Arrays.toString(a));
}
public static void sort(int[] arr) {
int length = arr.length;
//构建堆
buildHeap(arr,length);
for ( int i = length - 1; i > 0; i-- ) {
//将堆顶元素与末位元素调换
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
//数组长度-1 隐藏堆尾元素
length--;
//将堆顶元素下沉 目的是将最大的元素浮到堆顶来
sink(arr, 0,length);
}
}
private static void buildHeap(int[] arr, int length) {
for (int i = length / 2; i >= 0; i--) {
sink(arr,i, length);
}
}
private static void sink(int[] arr, int index, int length) {
int leftChild = 2 * index + 1;//左子节点下标
int rightChild = 2 * index + 2;//右子节点下标
int present = index;//要调整的节点下标
//下沉左边
if (leftChild < length && arr[leftChild] > arr[present]) {
present = leftChild;
}
//下沉右边
if (rightChild < length && arr[rightChild] > arr[present]) {
present = rightChild;
}
//如果下标不相等 证明调换过了
if (present != index) {
//交换值
int temp = arr[index];
arr[index] = arr[present];
arr[present] = temp;
//继续下沉
sink(arr, present, length);
}
}
}
八、计数排序 (Count Sort)
解释:统计序列中每个元素的出现次数,将元素映射到有序的桶中,最后按照桶的顺序输出元素,完成排序。
public class CountSort {
public static void main(String[] args) {
int[] array = { 4, 2, 2, 8, 3, 3, 1 };
// 找到数组中最大的值 ---> max:8
int max = findMaxElement(array);
int[] sortedArr = countingSort(array, max + 1);
System.out.println("计数排序后的数组: " + Arrays.toString(sortedArr));
}
private static int findMaxElement(int[] array) {
int max = array[0];
for (int val : array) {
if (val > max)
max = val;
}
return max;
}
private static int[] countingSort(int[] array, int range) { //range:8+1
int[] output = new int[array.length];
int[] count = new int[range];
//初始化: count1数组
for (int i = 0; i < array.length; i++) {
count[array[i]]++;
}
//计数: count2数组,累加次数后的,这里用count2区分
for (int i = 1; i < range; i++) {
count[i] = count[i] + count[i - 1];
}
//排序:最后数组
for (int i = 0; i < array.length; i++) {
output[count[array[i]] - 1] = array[i];
count[array[i]]--;
}
return output;
}
}
九、桶排序(Bucket Sort)
解释:将待排序序列均匀地分到若干个桶中,对每个桶中的元素进行排序,最后按照桶的顺序输出所有元素,完成排序。

public class BucketSort {
public static void sort(int[] arr){
//最大最小值
int max = arr[0];
int min = arr[0];
int length = arr.length;
for(int i=1; i<length; i++) {
if(arr[i] > max) {
max = arr[i];
} else if(arr[i] < min) {
min = arr[i];
}
}
//最大值和最小值的差
int diff = max - min;
//桶列表
ArrayList<ArrayList<Integer>> bucketList = new ArrayList<>();
for(int i = 0; i < length; i++){
bucketList.add(new ArrayList<>());
}
//每个桶的存数区间
float section = (float) diff / (float) (length - 1);
//数据入桶
for(int i = 0; i < length; i++){
//当前数除以区间得出存放桶的位置 减1后得出桶的下标
int num = (int) (arr[i] / section) - 1;
if(num < 0){
num = 0;
}
bucketList.get(num).add(arr[i]);
}
//桶内排序
for(int i = 0; i < bucketList.size(); i++){
//jdk的排序速度当然信得过
Collections.sort(bucketList.get(i));
}
//写入原数组
int index = 0;
for(ArrayList<Integer> arrayList : bucketList){
for(int value : arrayList){
arr[index] = value;
index++;
}
}
}
}
十、基数排序(Raix Sort)
解释:将待排序序列按照每一位数字的大小关系进行排序,从低位到高位进行多次排序,最终得到一个有序序列。

import java.util.Arrays;
public class RaixSort {
public static void main(String[] args) {
int[] arr = { 53, 3, 542, 748, 14, 214 };
// 得到数组中最大的数
int max = arr[0];// 假设第一个数就是数组中的最大数
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
// 得到最大数是几位数
// 通过拼接一个空串将其变为字符串进而求得字符串的长度,即为位数
int maxLength = (max + "").length();
// 定义一个二维数组,模拟桶,每个桶就是一个一维数组
// 为了防止放入数据的时候桶溢出,我们应该尽量将桶的容量设置得大一些
int[][] bucket = new int[10][arr.length];
// 记录每个桶中实际存放的元素个数
// 定义一个一维数组来记录每个桶中每次放入的元素个数
int[] bucketElementCounts = new int[10];
// 通过变量n帮助取出元素位数上的数
for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {
for (int j = 0; j < arr.length; j++) {
// 针对每个元素的位数进行处理
int digitOfElement = arr[j] / n % 10;
// 将元素放入对应的桶中
// bucketElementCounts[digitOfElement]就是桶中的元素个数,初始为0,放在第一位
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
// 将桶中的元素个数++
// 这样接下来的元素就可以排在前面的元素后面
bucketElementCounts[digitOfElement]++;
}
// 按照桶的顺序取出数据并放回原数组
int index = 0;
for (int k = 0; k < bucket.length; k++) {
// 如果桶中有数据,才取出放回原数组
if (bucketElementCounts[k] != 0) {
// 说明桶中有数据,对该桶进行遍历
for (int l = 0; l < bucketElementCounts[k]; l++) {
// 取出元素放回原数组
arr[index++] = bucket[k][l];
}
}
// 每轮处理后,需要将每个bucketElementCounts[k]置0
bucketElementCounts[k] = 0;
}
}
System.out.println(Arrays.toString(arr));//[3, 14, 53, 214, 542, 748]
}
}



