[poj2406]Power Strings
Description
对于两个字符串\(a,b\),定义\(a\;\times\;b\)为将\(b\)接到\(a\)的末尾组成新的字符串。对于一个字符串\(a\)的幂运算的定义与我们在数学中的定义一样:\(a^0=''\)(空字符),\(a^{n+1}=a^n\;\times\;a\)。
Input
输入数据每一行为一个字符串,长度为\(L\)。输入数据以\('.'\)结尾。
Output
对于每个字符串\(s\),输出最大的\(n\)使得字符串\(s\)满足条件:\(s=a^n\)(\(a\)为一个字符串)。
Sample Input
abcd
aaaa
ababab
.
Sample Output
1
4
3
HINT
\(1\;\leq\;L\;\leq\;10^6\)
Solution
题意就是给你一个字符串,求这个字符串是为哪个子串循环而成的,要求子串循环的次数最大。
因为是字符串,而且需要自我匹配,就会想到\(kmp\)的\(next[\;]\)。
然后通过一些模拟后发现,如果一个字符串\(s\)是有其长度为\(l\)的子串\(a\)循环而成的,则将\(s\)左移或右移\(l\)为后得到\(s'\),\(s'\)与\(s\)在第\(1\)~\(n-l\)位依然重合(如下图)。
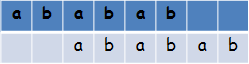
还有一个需要考虑的是,\(l\)必须为\(s\)的因数,否则无法形成\(s\)。
到这里,问题就基本解决了,具体细节参见代码。
#include<set>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<cstdio>
#include<vector>
#include<string>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 1000002
using namespace std;
int next[N],l[N],n,ans;
char a[N];
inline void get_next(){
for(int i=2,j=0;i<=n;i++){
while(j&&a[i]!=a[j+1]) j=next[j];
j+=(a[i]==a[j+1]);
next[i]=j;
}
}
inline bool chk(int k){
return !(n%(n-k));
}
inline void init(){
while(true){
scanf("%s",a+1);
n=strlen(a+1);
if(n==1&&a[1]=='.') break;
fill(next+1,next+1+n,0);
get_next();
for(ans=next[n];ans;ans=next[ans])
if(chk(ans)) break;
ans=n-ans;
printf("%d\n",n/ans);
}
}
int main(){
freopen("pow.in","r",stdin);
freopen("pow.out","w",stdout);
init();
fclose(stdin);
fclose(stdout);
return 0;
}


