[bzoj1912][Apio2010]patrol 巡逻
Description
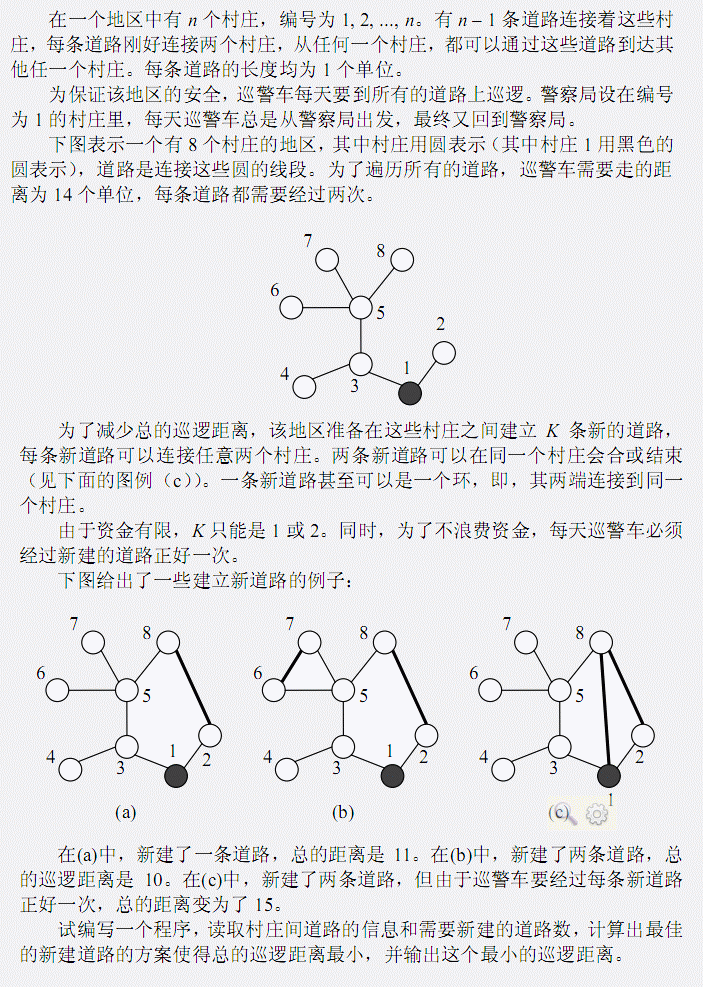
Input
第一行包含两个整数 n, K(1 ≤ K ≤ 2)。
接下来 n – 1行,每行两个整数 a, b,表示村庄a与b之间有一条道路(1 ≤ a, b ≤ n)。
Output
输出一个整数,表示新建了K 条道路后能达到的最小巡逻距离。
Sample Input
8 1
1 2
3 1
3 4
5 3
7 5
8 5
5 6
Sample Output
11
HINT
3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。
Solution
不建道路时方案数为2(n-1)。
建一条道路时,把树直径两段连上,答案为2(n-1)-r+1。
此基础上再建一条道路:把树直径删去,在现在的图上再求一条直径。
那么,\(k\leq10^5\)要怎么做呢?
#define N 100005
struct graph{
int nxt,to,w;
}e[N<<1];
int g[N],f1[N],f2[N],n,m,mx,id,ans,cnt=1;
bool vis[N];
inline void addedge(int x,int y){
e[++cnt].nxt=g[x];g[x]=cnt;e[cnt].to=y;e[cnt].w=1;
}
inline void adde(int x,int y){
addedge(x,y);addedge(y,x);
}
inline int dfs(int u,int fa){
int s1=0,s2=0;
for(int i=g[u],tmp;i;i=e[i].nxt)
if(e[i].to!=fa){
tmp=e[i].w+dfs(e[i].to,u);
if(tmp>s1){
s2=s1;s1=tmp;f2[u]=f1[u];f1[u]=i;
}
else if(tmp>s2){
s2=tmp;f2[u]=i;
}
}
if(s1+s2>mx) mx=s1+s2,id=u;
return s1;
}
inline void Aireen(){
n=read();m=read();
for(int i=1;i<n;++i)
adde(read(),read());
ans=(n-1)<<1;
while(m--){
memset(f1,0,sizeof(f1));
memset(f2,0,sizeof(f2));
mx=id=0;dfs(1,0);ans+=1-mx;
for(int i=f1[id];i;i=f1[e[i].to]) e[i].w=e[i^1].w=-1;
for(int i=f2[id];i;i=f1[e[i].to]) e[i].w=e[i^1].w=-1;
}
printf("%d\n",ans);
}
2017-05-03 22:23:28

![[bzoj1912][Apio2010]patrol 巡逻](https://img2022.cnblogs.com/blog/958077/202201/958077-20220127005216215-719095766.png) 如图.
如图.

