ICPC2019-HK

G

Description

对于一棵树，可以选一些点放置障碍，希望所有叶子到根的路径上都有障碍且被放置障碍的点权和最小。
给定最优方案数K(\(10^9\)量级），希望给出一棵满足要求的树（要求树的大小不超过\(10^5\))。

Solution

• 不考虑树大小的限制，对于任意K构造以下树即可：
  

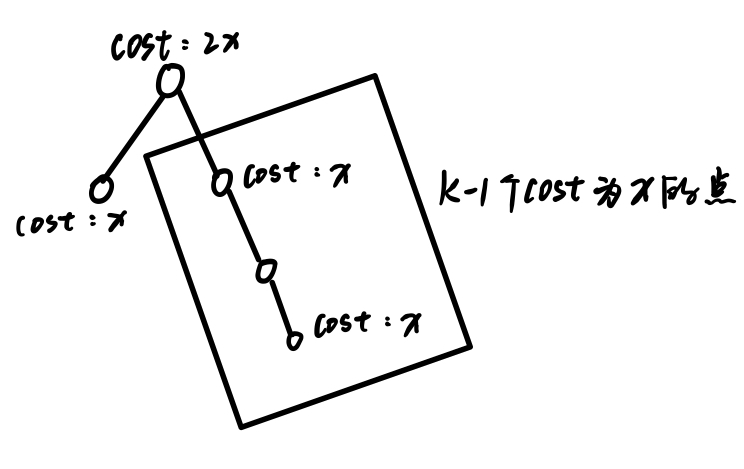
• 考虑到树大小的限制，我们令\(K=K1\times K2+K3\;(K1=\lfloor\sqrt{K}\rfloor,\;K3=K\;mod\;K1)\)，那么树大小为K1+K2+K3（大约为\(3\sqrt{K}\)，树形态如下：
  

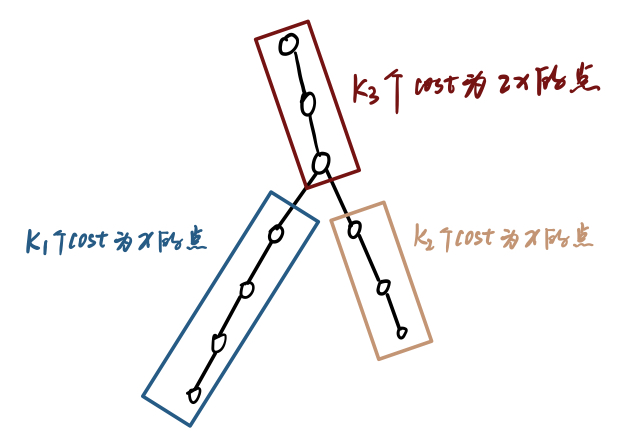
E

Description

给定一个长度为n且元素互不相同的数组，每次可以任选数组中连续的三个数，将三个数中的最小数和最大数删掉，重复操作直至只剩一个数。问数组中哪些数有可能留到最后。

Solution

观察到n的规模支持\(O(n^2)\)的算法，所以考虑对每个数进行判定。
（假定现在判定的数为x)
显而易见的是，当只剩三个数且x的大小在中间，那么x能留到最后。(情况(1))
观察到，对于任意一种满足 比x大的数（称为L）的个数=比x小的数（称为S）的个数 的情况，都能消成情况(1)，因为每次都能找到同时包含L和S的连续的三个数，然后消去L和S各一个。
那么我们只需判定能否有一种消法使得L和S的个数相等。
（假定现在L的个数>S，我们需要减少L的个数）

• 对于连续的个数\(\geq3\)的一串L，我们可以两个两个地消去。
• 对于S，我们可以将它与它前面的L一起消掉，让后面出现新的L串时，可以与前面剩余的L串连在一起消。

记录最多可以比S多消去几个L，即可知道能否有一种消法使得L和S的个数相等。

code

#include<bits/stdc++.h>
using namespace std;
const int N=5005;
int a[N],ans[N],n;
int chk(int x){
//	printf("chk(%d)\n",x);
	int del=abs((n-a[x])-(a[x]-1));
	if(!del) return 1;
	int del_type=a[x]<=(n/2)?1:0;
	for(int i=1,tot=0,type;i<x;++i){
		type=a[i]<a[x]?0:1;
		if(type==del_type) ++tot;
		else if(tot) --tot;
		
		if(tot>=3){
			tot-=2;del-=2;
		}
		if(!del) return 1;
	}
	for(int i=x+1,tot=0,type;i<=n;++i){
		type=a[i]<a[x]?0:1;
		if(type==del_type) ++tot;
		else if(tot) --tot;
		
		if(tot>=3){
			tot-=2;del-=2;
		}
		if(!del) return 1;
	}
	
	return (!del)?1:0;
}
int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		scanf("%d",&n);
		for(int i=1;i<=n;++i)
			scanf("%d",&a[i]);
		for(int i=1;i<=n;++i)
			printf("%d",chk(i));
		printf("\n");
	}
	return 0;
}