[学习笔记]FFT
多项式
\(n\)次多项式 \(f(x)=\sum_{i=0}^{n}a_ix^i,a_i\)为系数.
系数表示
系数组成的 \(n+1\) 维向量.
点值表示
取 \(n+1\) 互不相同的\(x_i\)代入多项式, 取到 \(n+1\) 个值, 称为点值表示.
通过 \(n+1\) 个值可以求出唯一确定的多项式(插值法).
复数
设 \(i=\sqrt{-1}\), 表示虚数单位.
设 \(a,b\in{R}\), 形如 \(a+bi\) 的数表示复数.
复平面
复平面
\(x\)轴表示实数, \(y\)轴表示复数, \(a+bi\) 对应复平面上从\((0,0)\)指向\((a,b)\)的一个向量.
模长
向量长度\(\sqrt{a^2+b^2}\).
幅角
从\(x\)轴正方向到该向量的转角角度(以逆时针为正方向).
计算
复数相加: 四边形定则.
复数相乘: 模长相乘,幅角相加.
单位根
n次单位根
满足方程 \(x^n=1\) 的复数,一共有\(n\)个, 构成复平面上的单位圆的\(n\)个\(n\)等分点.
根据复数乘法可得, \(n\)次单位根的模长为 \(1\) , 幅角的\(n\)倍为 \(0\) ,
设 \(\theta=\frac{2\pi}{n},\omega_n^k(0\leq{k}<n,k\in{N})\) 表示\(n\)个根, 则 \(\omega_n^k=cos(k\cdot\theta)+i\times{sin(k\cdot\theta)}\).
性质
- \(\omega_{2n}^{2k}=\omega_n^k\).
二者几何表示终点相同,即
\(\begin{split}\omega_{2n}^{2k}&=cos(2k\cdot\frac{2\pi}{2n})+i\times{sin(2k\cdot\frac{2\pi}{2n})}\\&=cos(k\cdot\frac{2\pi}{n})+i\times{sin(k\cdot\frac{2\pi}{n})}\\&=\omega_n^k\end{split}\)
- \(\omega_{n}^{k+\frac{n}{2}}=-\omega_n^k\)
\(\omega_{n}^{k+\frac{n}{2}}=\omega_{n}^{k}\times\omega_{n}^{\frac{n}{2}}\)
\(\begin{split}\omega_{n}^{\frac{n}{2}}&=cos(\frac{n}{2}\cdot\frac{2\pi}{n})+i\times{sin(\frac{n}{2}\cdot\frac{2\pi}{n})}\\&=cos\pi+i\times{sin\pi}\\&=-1\end{split}\)
多项式乘法
给定两个多项式\(A(x),B(x),A(x)=\sum_{i=0}^{n}a_ix^i,B(x)=\sum_{i=0}^{n}b_ix^i\).
\(\begin{split}C(x)&=A(X)\times{B(x)}\\&=\sum_{i=0}^{2n}c_ix^i\\&=\sum_{i=1}^{2n}\sum_{j=0}^{min(i,n)}a_jb_{i-j}\end{split}\)
直接计算的话, 需要\(O(n^2)\)的时间复杂度.
但如果能找到一种方式转化成点值表示(只有 \(n+1\) 个点), 就可以用\(O(n)\)的时间复杂度得到\(c_i\)了.
快速傅里叶变换
分为 \(DFT,IDFT\), 分别用于在\(O(n\;logn)\)的时间内实现系数表示到点值表示, 点值表示到系数表示.
离散傅里叶变换(DFT)
对于 \(n-1\) 次多项式 \(f(x)=\sum_{i=0}^{n-1}a_ix^i\)(若\(n\)不是\(2\)的幂次,高次系数用\(0\)补).
将\(n\)次单位根的 \(0\) 到 \(n−1\) 次幂\(\omega_n^0\dots\omega_n^{n-1}\)代入多项式的系数表示, 得到点值向量\(f(\omega_n^0)\dots{}f(\omega_n^{n-1})\).
此时直接计算还需\(O(n^2)\).
将系数奇偶分类:
\(f(x)=(a_0+a_2x^2+...a_{n-2}a^{n-2})+(a_1x+a_3x^3+...a_{n-1}a^{n-1})\).
设 \(f_1(x)=a_0+a_2x+...a_{n-2}x^{\frac{n}{2}-1}\\f_2(x)=a_1+a_3x+...a_{n-1}x^{\frac{n}{2}-1}\)
则 \(f(x)=f_1(x^2)+xf_2(x^2).\)
利用单位根性质,
对于 \(\omega_{n}^{k}(k<\frac{n}{2})\),
\(\begin{split}f(\omega_{n}^{k})&=f_1(\omega_{n}^{2k})+\omega_{n}^{k}f_2(\omega_{n}^{2k})\\&=f_1(\omega_{\frac{n}{2}}^{k})+\omega_{n}^{k}f_2(\omega_{\frac{n}{2}}^{k})\end{split}\)
对于\(\omega_{n}^{k+\frac{n}{2}}\),
\(\begin{split}f(\omega_{n}^{k+\frac{n}{2}})&=f_1(\omega_{n}^{2k+n})+\omega_{n}^{k+\frac{n}{2}}f_2(\omega_{n}^{2k+n})\\&=f_1(\omega_{n}^{2k}\cdot\omega_{n}^{n})-\omega_n^kf_2(\omega_{n}^{2k}\cdot\omega_{n}^{n})\\&=f_1(\omega_{n}^{2k})-\omega_n^kf_2(\omega_{n}^{2k})\\&=f_1(\omega_{\frac{n}{2}}^{k})-\omega_n^kf_2(\omega_{\frac{n}{2}}^{k})\end{split}\)
此时只需代入\(\omega_{\frac{n}{2}}^{0}\dots\omega_{\frac{n}{2}}^{\frac{n}{2}-1}\), 就可求出\(\omega_{n}^{0}\dots\omega_{n}^{n-1}\)
复杂度就降成了\(O(n\;logn)\).
傅立叶逆变换(IDFT)
设 \(y_i=f(\omega_n^i)=\sum_{j=0}^{n-1}a_j(\omega_n^i)^j,g(x)=\sum_{i=1}^{n-1}y_ix^i\)
\(b_k=g(\omega_n^{-k})=\sum_{i=0}^{n-1}y_i(\omega_n^{-k})^i,b_k\)为 \(\omega_n^{-k}\) 的点值表示.
设\(s(\omega_n^k)=\sum_{i=0}^{n-1}(\omega_n^k)^i=\frac{1-(\omega_n^k)^n}{1-\omega_n^k}\)(等比数列求和).
当 \(k=0\) 时, \(\omega_n^0=1,s(\omega_n^k)=n\);
当 \(0<k<n\) 时, \((\omega_n^k)^n=1\), \(s(\omega_n^k)=0\).
\(\begin{split}b_k&=\sum_{i=0}^{n-1}y_i(\omega_n^{-k})^i\\&=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j(\omega_n^i)^j(\omega_n^{-k})^i\\&=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j(\omega_n^{j-k})^i\\&=\sum_{j=0}^{n-1}a_j\sum_{i=0}^{n-1}(\omega_n^{j-k})^i\\&=\sum_{j=0}^{n-1}a_j\times{s(\omega_n^{j-k})}\\&=a_k\times{n}\end{split}\)
所以,\(a_k=\frac{c_k}{n}\).
以单位根的倒数代替单位根做一次 \(DFT\), 结果\(/n\)就行了.
模板
#define M 800005
typedef long double ld;
const ld pi=acos(-1.0);
struct cp{
ld x,y;
cp() {}
cp(ld x,ld y):x(x),y(y) {}
friend cp operator + (cp a,cp b){
return cp(a.x+b.x,a.y+b.y);
}
friend cp operator - (cp a,cp b){
return cp(a.x-b.x,a.y-b.y);
}
friend cp operator * (cp a,cp b){
return cp(a.x*b.x-a.y*b.y,a.y*b.x+a.x*b.y);
}
};
namespace FFT{
int re[M],n;cp w[2][M];
inline void init(int k){
k<<=1;n=1;while(n<k) n<<=1;
for(int i=0;i<n;++i){
w[0][i]=cp(cos(pi*2/n*i),sin(pi*2/n*i));
w[1][i]=cp(w[0][i].x,-w[0][i].y);
}
k=0;while((1<<k)<n) ++k;
for(int i=0,t;i<n;++i){
t=0;
for(int j=0;j<k;++j)
if(i&(1<<j)) t|=(1<<k-j-1);
re[i]=t;
}
}
inline void DFT(cp *a,int ty){
cp *o=w[ty];
for(int i=0;i<n;++i)
if(i<re[i]) swap(a[i],a[re[i]]);
cp tmp;
for(int l=2,m;l<=n;l<<=1){
m=l>>1;
for(cp *p=a;p!=a+n;p+=l)
for(int i=0;i<m;++i){
tmp=o[n/l*i]*p[i+m];
p[i+m]=p[i]-tmp;p[i]=p[i]+tmp;
}
}
if(ty) for(int i=0;i<n;++i)
a[i].x/=(ld)(n),a[i].y/=(ld)(n);
}
}
// C(x)=A(x)*b(x)
inline void Aireen(){
for(int i=0;i<n;++i)
a[i]=cp((ld)(read()),0.0),b[i]=cp((ld)(read()),0.0);
FFT::init(n);
FFT::DFT(a,0);FFT::DFT(b,0);
for(int i=0;i<FFT::n;++i)
c[i]=a[i]*b[i];
FFT::DFT(c,1);
}
卷积
给定两个定义域 \(\in{N}\) 的函数 \(f(x),g(x)\),
定义它们的卷积为 \((f*g)(n)=\sum_{i=0}^{n}f(i)g(n-i)\).
对比多项式乘法:\(C(x)=A(x)\times{B(x)},c_i=\sum_{j=0}^{i}a_j\times{b_{i-j}}\)
可以发现 \(c_i=(A*B)(i)\).
至此,就可以用 \(FFT\) 优化卷积了.
循环卷积
首先对于一个一一对应的序列,
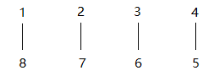
将其卷积后:
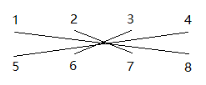
将其左移两位后:
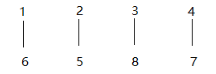
卷积为:
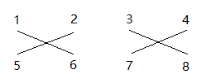
通过观察可以发现,循环卷积也就是将前 \(i\) 个系数做一次卷积 \(+\) 后 \(n-i-1\) 个系数做一次卷积.
2017-04-19 15:31:18


 浙公网安备 33010602011771号
浙公网安备 33010602011771号