[学习笔记]计算几何基础

三角函数

\(\;\)	0°	30°	45°	60°	90°
\(sin\alpha\)	0	\(\frac{1}{2}\)	\(\frac{\sqrt{2}}{2}\)	\(\frac{\sqrt{3}}{2}\)	1
\(cos\alpha\)	1	\(\frac{\sqrt{3}}{2}\)	\(\frac{\sqrt{2}}{2}\)	\(\frac{1}{2}\)	\(0\)
\(tan\alpha\)	\(0\)	\(\frac{\sqrt{3}}{3}\)	\(1\)	\(\sqrt{3}\)	不存在
\(cot\alpha\)	不存在	\(\sqrt{3}\)	\(1\)	\(\frac{\sqrt{3}}{3}\)	0

向量

线性空间中有大小和方向的量.

坐标表示:\(\small{P(x_1,y_1),Q(x_2,y_2)}\).

\(\small{\overrightarrow{PQ}=(x_2-x_1,y_2-y_1)}\).

\(\small{|PQ|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}\).

struct point{
    int x,y;
}

向量运算

\(a=(x_1,y_1),b=(x_2,y_2)\).

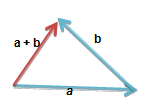
加法

\(a+b=(x_1+x_2,y_1+y_2)\).

inline point add(point a,point b){
    return (point){a.x+b.x,a.y+b.y};
}

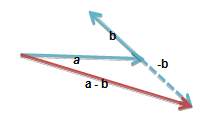
减法

\(a-b=(x_1-x_2,y_1-y_2)\).

inline point dec(point a,point b){
    return (point){a.x-b.x,a.y-b.y};
}

点乘

\(a\;\cdot\;b=x_1x_2+y_1y_2\).

\(a\;\cdot\;b=|a||b|cos<a,b>\)

应用:求两向量夹角,判断是否垂直(\(cos90\)°\(=0\)).

inline int dot(point a,point b){
    return a.x*b.x+a.y*b.y;
}

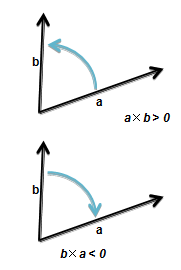
叉乘

\(a\;\times\;b=x_1y_2-x_2y_1\).

\(|a\;\times\;b|=|a||b|sin<a,b>\).

\(a\;\times\;b=0\),共线.

inline int mul(point a,point b){
    return a.x*b.y-a.y*b.x;
}

向量旋转

将\(a(x_1,y_1)\)逆时针旋转\(\theta\)(弧度)得到\(b(x_1cos\theta-y_1sin\theta,x_1sin\theta+y_1cos\theta)\).

\(P.S.\)只改变方向(长度不变).
记忆方法:旋转\(\pi/2\)得到的结果\((-y_1,x_1)\).

三点共线

夹角为\(0\)且\(a\;\times\;b=0\).

点是否在射线上

夹角为\(0\)且点乘\(\geq\;0\).

\(<0\)则为方向延长线上的点.

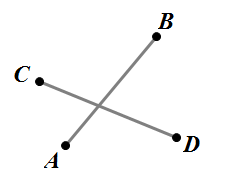
判断线段交

\(\small{(\overrightarrow{AC}\times\overrightarrow{AD})(\overrightarrow{BC}\times\overrightarrow{BD})\leq0}\)且\(\small{(\overrightarrow{CA}\times\overrightarrow{CB})(\overrightarrow{DA}\times\overrightarrow{DB})\leq0}\).

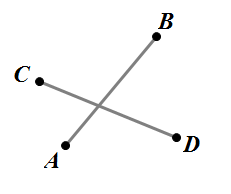
两直线求交点

\(\small{C(x_1,y_1),D(x_2,y_2)}\)

\(s_1\small{=\overrightarrow{AB}\;\times\;\overrightarrow{AC}},\;s_2\small{=\overrightarrow{AD}\;\times\;\overrightarrow{AB}}\)

交点为\(\large{(\frac{x_1s_2+x_2s_1}{s_1+s_2},\frac{y_1s_2+y_2s_1}{s_1+s_2})}\)

inline point inter(line a,line b){
    ld s1,s2,t;point ret;
    s1=mult(dec(b.e,a.s),dec(a.e,a.s));
    s2=mult(dec(a.e,a.s),dec(b.s,a.s));
    t=s2/(s1+s2);
    ret.x=b.s.x+(b.e.x-b.s.x)*t;
    ret.y=b.s.y+(b.e.y-b.s.y)*t;
    return ret;
}

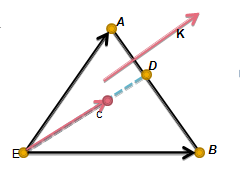
点到直线垂足

点到直线垂足\(\small{D,ED\;}\perp\small{\;AB}\).

旋转\(\small{\overrightarrow{AB}}\;\;\pi/2\),直线求交.

圆的位置关系

\(d\)为两圆圆心距,\(R,r\)分别为两圆半径.

\(d>R+r\) 外离;

\(d=R+r\) 外切;

\(|R – r|<d<R+r\) 相交;

\(d=|R–r|\) 内切;

\(d<|R–r|\) 内含.

点是否在凸多边形内

转角法.

inline point dec(point x,point y){
    return (point){x.x-y.x,x.y-y.y};
}
inline double mul(point x,point y){
    return x.x*y.y-y.x*x.y;
}
inline bool onseg(point p,point a,point b){  
    if(cmp(mul(dec(a,p),dec(b,p)))) return false;  
    return cmp(a.x-p.x)*cmp(b.x-p.x)<=0&&cmp(a.y-p.y)*cmp(b.y-p.y)<=0;
} 
inline int chk(point p){
    int cnt=0,k,d1,d2;
    for(int i=1;i<=n;++i){
        if(onseg(p,a[i],a[i+1])) return -1;
        k=cmp(mul(dec(a[i+1],a[i]),dec(p,a[i])));
        d1=cmp(a[i].y-p.y);d2=cmp(a[i+1].y-p.y);
        if(k>0&&d1<=0&&d2>0) ++cnt;
        if(k<0&&d2<=0&&d1>0) --cnt;
    }
    if(cnt) return 1;
    return 0;
}

多边形面积

设多边形顶点依次为\(\small{P_1,P_2,...,P_n}\).

\(S=\large{|\frac{\sum_{i=1}^{n-1}\overrightarrow{OP_i}\times\overrightarrow{OP_{i+1}}\;+\;\overrightarrow{OP_n}\times\overrightarrow{OP_{1}}}{2}}|\).

#define N 100005
struct point{
	int x,y; 
}a[N];
int n;
inline int mul(point x,point y){
	return x.x*y.y-x.y*y.x;
}
inline double area(){
	int ret=0;
	a[n+1]=a[1];
	for(int i=1;i<=n;i++)
		ret+=mul(a[i],a[i+1]);
	return fabs((double)(ret)/2.0);
}