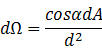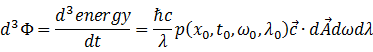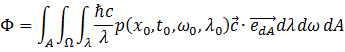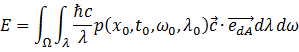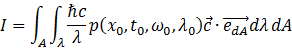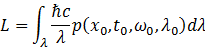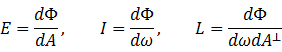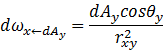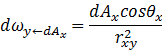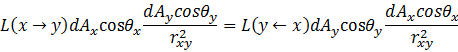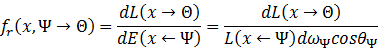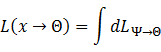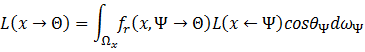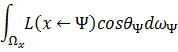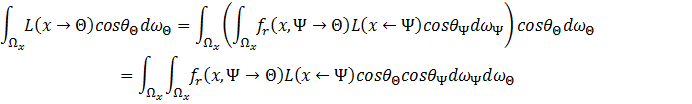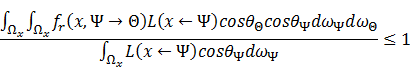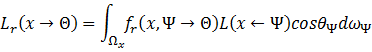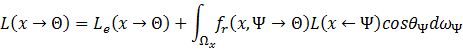全局照明算法基础——从辐射亮度到渲染方程
全局照明(Global Illumination)问题上已经有很多著名的算法,如路径追踪(Path Tracing),辐照度(Radiosity)等。绝大部分书籍/教材都直接介绍了做法,在理论方面有所欠缺(比如算法的正确性)。这段时间在看《Advanced Global Illumination》,大呼爽快,所以做了这些笔记。
一、方向和立体角
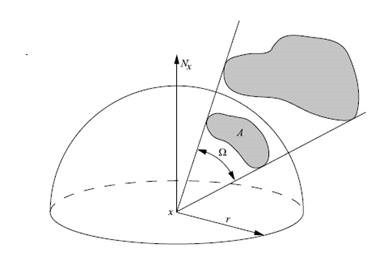
立体角(Solid Angle)是平面角的推广。如上图,考虑一块不规则的曲面,其在单位球体(球心在原点,半径![]() )上的投影为曲面
)上的投影为曲面![]() ,则
,则![]() 的面积
的面积![]() 为该曲面对应的立体角
为该曲面对应的立体角![]() 。根据定义易知,任何包含原点的球体对应的立体角都为
。根据定义易知,任何包含原点的球体对应的立体角都为![]() 。如果用球坐标
。如果用球坐标![]() 来刻画立体角,那么其微分
来刻画立体角,那么其微分![]() 可以被表示为
可以被表示为
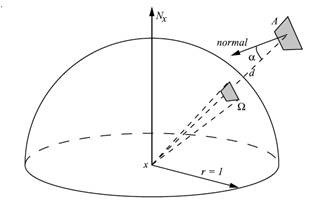
此外,根据立体角的定义,可以给出任何曲面元对应立体角的计算公式——
其示意图如下:
二、Radiance的定义
考虑密度函数![]() ,它给出在时空坐标
,它给出在时空坐标![]() 处单位体积内沿方向
处单位体积内沿方向![]() 、波长为
、波长为![]() 的光子的数量。那么给定位置
的光子的数量。那么给定位置![]() 、时间
、时间![]() 、方向
、方向![]() 以及波长
以及波长![]() ,容易知道单位时间内沿方向
,容易知道单位时间内沿方向![]() 通过面元
通过面元![]() 的、波长在
的、波长在![]() 间的光子的能量为
间的光子的能量为
其中![]() 是这些光子的速度。在波长范围
是这些光子的速度。在波长范围![]() 、全体立体角
、全体立体角![]() 、曲面
、曲面![]() 上对
上对![]() 积分得
积分得
类似地,定义辐射照度(Irradiance)为
辐射强度(Intensity)为
以及辐射亮度(Radiance)——
这几个量间有以下关系:
三、Radiance的守恒性质
从![]() 的定义可知,Radiance是空间位置和方向的函数可以写作
的定义可知,Radiance是空间位置和方向的函数可以写作![]() ,表示从空间位置
,表示从空间位置![]() 出发、朝向
出发、朝向![]() 的Radiance。(类似地,
的Radiance。(类似地,![]() 表示空间位置
表示空间位置![]() 处朝方向
处朝方向![]() 的Radiance)若
的Radiance)若![]() 与
与![]() 间没有遮挡,则有以下重要性质成立:
间没有遮挡,则有以下重要性质成立:
证明:
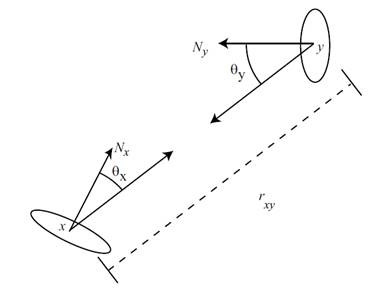
如上图,由Radiance的定义有
其中![]() 是从
是从![]() 出发向
出发向![]() 发射的能量。根据能量守恒,它们必定都被
发射的能量。根据能量守恒,它们必定都被![]() 接收,即
接收,即
又由立体角的性质
代入得
四、以Radiance来量度传感设备响应
摄像机、人眼等感光设备所得到的光的量度可以用Radiance来衡量,而非Flux等。由此可以得出一些结论,比如一个明亮的物体随着观察者距离的增加不会显得更暗,这是因为在光的传播过程中Radiance不随距离改变。
五、BRDF
一束光照射到某个表面上,反射的效果随着表面的材质有所不同。譬如,理想的镜子会把所有的入射光反射到某个特定的方向,而在其他方向上的反射光为0;理想的Lambertian表面会把入射光往所有的方向均匀地反射。反射光在不同方向上的多少分布,再结合入射光的方向所构成的函数,称为bidirectional reflectance distribution function(BRDF),记作![]() ,表示沿
,表示沿![]() 方向照射到
方向照射到![]() 处的光在
处的光在![]() 方向上的分布。准确地说:
方向上的分布。准确地说:
并非所有的物体表面的反射都能用BRDF来建模,譬如通透的玉石(入射光可以从某一处进入玉石内部,然后从另一处穿出)等。一个把透明物体的表面纳入考虑的函数叫做bidirectional scattering distribution function(BSDF),它描述了所有方向的入射光和出射光的分布;Bidirectional surface scattering reflectance distribution function(BSSRDF)则更加强大(使用起来也更为困难),它可以描述前面提到的通透的玉石对光的作用。在这里,为了简化问题,假设所有的物体表面都使用BRDF描述。
六、BRDF的几个性质
由BRDF的性质可知,某不透明的、不发光的表面上某一点![]() 处朝
处朝![]() 的Radiance是此点反射外来光的结果,可表示为
的Radiance是此点反射外来光的结果,可表示为
于是,
该式在之后会介绍的渲染方程中扮演了重要的角色。
Reciprocity:规定任意BRDF满足![]() ,由此,不妨将BRDF记作
,由此,不妨将BRDF记作![]() 。
。
能量守恒:单位面积的入射能量为
而单位面积反射的总能量为
于是由能量守恒:
七、渲染方程(The Rendering Equation)
![]() 可以被分为两部分:
可以被分为两部分:![]() 处自身向
处自身向![]() 方向发出的光和
方向发出的光和![]() 点反射外来光产生的光。即
点反射外来光产生的光。即
其中![]() 是自发光项,
是自发光项,![]() 是反射项。根据6中的推导,反射项
是反射项。根据6中的推导,反射项![]() 可以被表示为
可以被表示为
代入得
这就是所谓的渲染方程。可以看到该方程是递归的,且包含了一个不易计算的积分(只有在某些极简单的场景下才能求出解析解)。几乎所有的全局照明算法都是在求解渲染方程,因此称其为图形学的理论基石之一也不为过。