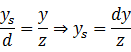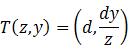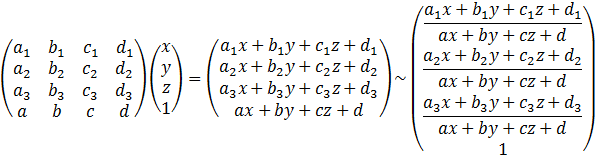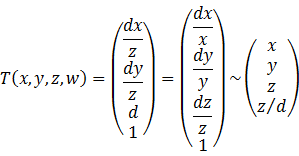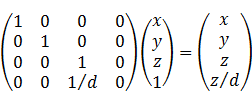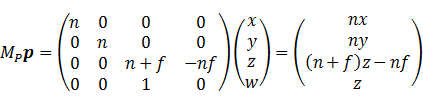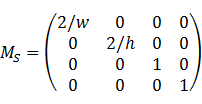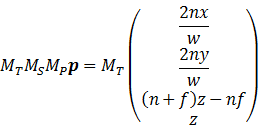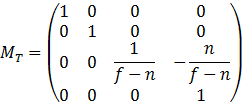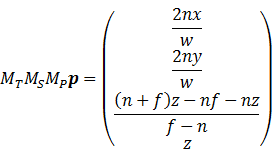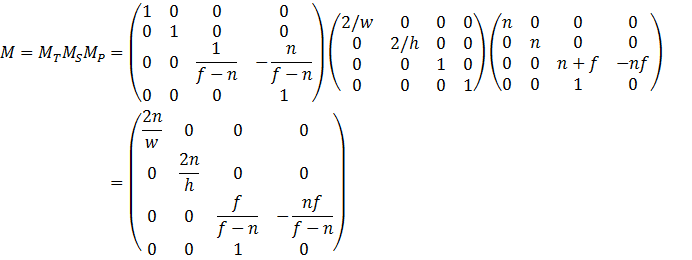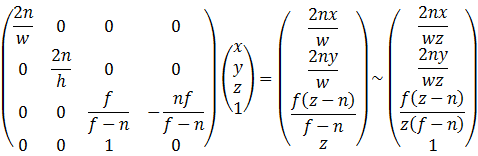透视投影矩阵推导
计算机图形学中,建模自小孔成像原理的透视摄像机是常用的摄像机模型。然而,由于光栅化渲染中的几何变换多基于四阶方阵与齐次坐标表示的向量的乘法,而四阶方阵只能表示仿射变换,无法实现透视摄像机“近大远小”的特性(仿射变换维持平行线相互平行,而“近大远小”不具有该性质),因此透视摄像机模型的实现要多费一番功夫。
1. 基本原理
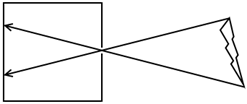
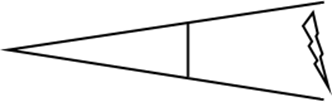
小孔成像是大多数人所熟知的最简单的成像原理之一,而常用的透视摄像机就是把小孔和屏幕(成像平面)的顺序交换,维持相似关系不变,因而这一模型达到了拟真的效果而被广泛应用。
小孔成像与简单的透视摄像机模型
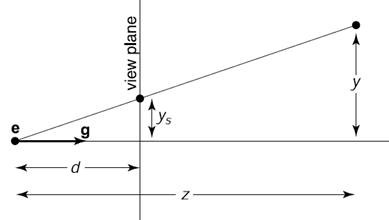
透视摄像机模型用在光栅化渲染管线的结果,就是透视投影过程。考虑简图——
图中从e点(原点)发出的一条射线上所有在view plane之后的点都被投影到view plane与该射线的交点。由相似关系显然有
这就得到了所需的映射关系:
显然![]() 并非仿射变换,也就不能直接借助四阶方阵乘法来实现。这时齐次坐标表示的另一个作用就表现出来了,设齐次坐标
并非仿射变换,也就不能直接借助四阶方阵乘法来实现。这时齐次坐标表示的另一个作用就表现出来了,设齐次坐标![]() 表示点
表示点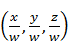 ,定义全体
,定义全体![]() 的齐次坐标上的等价关系:
的齐次坐标上的等价关系:![]() 当且仅当
当且仅当![]() ,则有
,则有![]() ,该式的右边正是常用的齐次坐标中点的表示方法(
,该式的右边正是常用的齐次坐标中点的表示方法(![]() )。这样一来,这一等价关系为我们提供了“除法”的能力,也扩充了仿射变换的能力。注意到,仿射变换可以将
)。这样一来,这一等价关系为我们提供了“除法”的能力,也扩充了仿射变换的能力。注意到,仿射变换可以将![]() 、
、![]() 、
、![]() 中的任意一个分量设置为
中的任意一个分量设置为![]() ,而该方法允许这样的变换形式——
,而该方法允许这样的变换形式——
注意到透视投影需要的变换是(假设viewing transform后摄像机面向+z方向)
这就是齐次坐标投影的基本原理。
2. 完整的投影矩阵推导
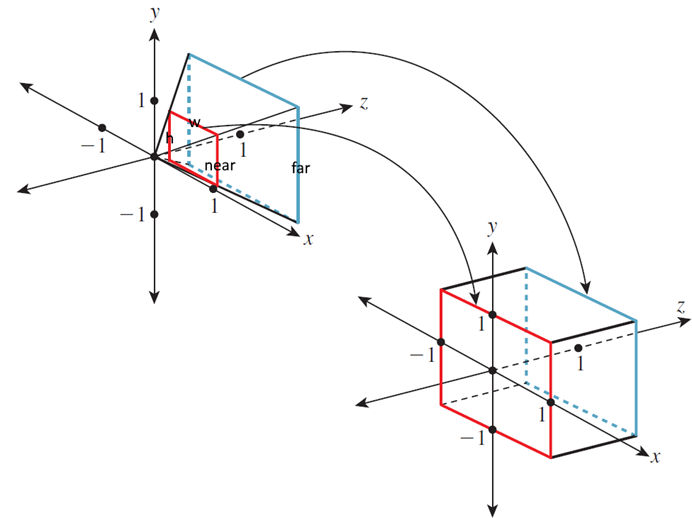
现实中使用的投影矩阵因为考虑了摄像机视截体,形式更加复杂。考虑下图中的透视投影变换——
显然该变换把近平面(near plane)区域投影到xOy平面上的单位正方形。在这里可以把该变换过程拆分成三个子过程:完成“透视”投影、把near plane上的视窗变换为单位正方形、把near plane的z坐标变换为0。第一个过程可以利用矩阵乘法:
其中n与f分别是视截体近平面与远平面与原点的距离。![]() 的第三行有些特殊。它的作用是保持被投影到near plane上同一点的各点间的深度关系不变(这样才能在稍后做depth test)。此外,由于
的第三行有些特殊。它的作用是保持被投影到near plane上同一点的各点间的深度关系不变(这样才能在稍后做depth test)。此外,由于![]() (齐次化过程),位于near plane上的点的
(齐次化过程),位于near plane上的点的![]() 、
、![]() 坐标都不会变化。
坐标都不会变化。
然后把near plane上的有效区域变换为单位正方形。假设near plane上有效区域的宽度为![]() ,高度为
,高度为![]() ,则一个简单的scaling即可解决问题——
,则一个简单的scaling即可解决问题——
再把near plane挪到xOy平面上,一个平移就能解决问题;另外深度的变化范围应该被固定在0~1之间。注意到
故只需要令
即可得
最后是一直没有进行的齐次化过程,即
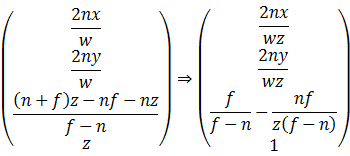
这就求得了所需的透视投影变换矩阵——
验证一下:
满足透视投影的要求。使用时,只需要将![]() 乘上待投影的坐标,再齐次化即可。
乘上待投影的坐标,再齐次化即可。
3. 其他
在一些别的条件/要求下,透视投影矩阵可能具有与此稍微不同的形式。譬如,OpenGL采用右手系,通常其viewing transform把坐标变换到camera space,其中camera是指向-z的(本例使用的是+z);此外,OpenGL中的z值被映射到-1~+1(本例使用的是0~1),但是,总体的推导思路是相同的。可以证明
是一个满足这些要求的投影矩阵(这里,l、r、t、b是视截体近平面的左、右、上、下坐标,本例中没有考虑这种不对称的情况)。
posted on 2017-02-04 16:36 AirGuanZ 阅读(24428) 评论(4) 编辑 收藏 举报