【数论】POJ1845 Sumdiv

最近本渣渣做了一道快搞死我的题，就是这个！

下面隆重给出题目以及链接：

Sumdiv

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 29696		Accepted: 7312

Description

Consider two natural numbers A and B. Let S be the sum of all natural divisors of A^B. Determine S modulo 9901 (the rest of the division of S by 9901).

Input

The only line contains the two natural numbers A and B, (0 <= A,B <= 50000000)separated by blanks.

Output

The only line of the output will contain S modulo 9901.

Sample Input

2 3

Sample Output

15

Hint

2^3 = 8. 
The natural divisors of 8 are: 1,2,4,8. Their sum is 15. 
15 modulo 9901 is 15 (that should be output). 

 

题目一眼就能看懂对吧？？不就是求A^B所有因子的和嘛！我第一眼看到题目这么短就心知不好，绝对有坑啊！！搜了一下，竟然要用到数论的知识，学离散的时候数论就学的不好，为了做这道题，把离散初等数论的章节又从头到尾复习了一遍。下面罗列一下这道题要用到的知识点：

 

埃氏筛法

这是里面最简单的一个知识点了！关于埃氏筛法前几天刚好写了篇随笔，可以戳一下看看。在这里是用来筛素的，提供一个素数表，方便后面的计算。

这是模板：

//埃氏筛法筛素
const int MAX_N = 10005;
int prime[MAX_N];
bool is_prime[MAX_N];
void getPrime(){
    int p = 0;
    for(int i = 2; i < MAX_N; i++) is_prime[i] = true;
    for(int i = 2; i < MAX_N; i++){
        if(is_prime[i]){
            prime[p++] = i;
            for(int j = 2*i; j < MAX_N ; j+=i) is_prime[j] = false;
        }
    }
}

 

 

算术基本定理

这也是数论里的一个知识点：任何大于1的整数要么是素数，要么可以分解成素数的乘积，这样的分解是唯一的。

也就是说，题目中的A，我们可以把它分解成这样的形式：A = p₁^k₁ * p₂^k₂ ... * p_n^k_n   (p_i是素数且k_i>0)

比如36，我们可以把它分解2² * 3²，其中的2和3都是素数；再比如44，我们可以把它分解成2² * 11¹，其中的2和11都是素数。

把这个弄懂之后，显然可以得到：A^B = p₁^k₁B * p₂^k₂B ... * p_n^k_nB   (p_i是素数且k_i>0）

下面是代码，我们要得到 p_i 以及 k_i 的数组，以及A的素因子的个数，方便后面的计算：

//素因子分解 
int p[MAX_N],k[MAX_N];
int cnt;
void getFactors(long long x){
    memset(k,0,sizeof(k));
    cnt = 0;
    for(int i = 0; prime[i]*prime[i] <=x ; i++){
        if(x % prime[i] == 0){ 
            p[cnt] = prime[i];
            while(x % prime[i] == 0){
                k[cnt]++;
                x /= prime[i];
            }
            cnt++;
        }
    }
    if(x != 1){   
        p[cnt] = x;
        k[cnt++] = 1;
    }
}

可能有人（本渣渣）会觉得奇怪，最后那步x！=1是怎么回事呢？注意，在前面for循环的部分，循环条件写的是prime[i]*prime[i]<=x，也就是说，我们只考虑了小于等于√x的素因子。而x最多只可能有一个大于√x的素因子（由算术基本定理，x可以分解为素数的乘积，若有两个大于√x的素因子，那么乘积将大于x），所以x除以√x范围内的所有素因子后如果仍不为1，那么此时剩下的x一定是一个素数，即最后一个素因子。

 

约数和定理

对于已经分解的整数 A = p₁^k₁ * p₂^k₂ ... * p_n^k_n   (p_i是素数且k_i>0)

有A的所有因子之和为 S = (p₁⁰+p₁¹+p₁²+...p₁^k₁) * (p₂⁰+p₂¹+p₂²+...p₂^k₂) ... * (p_n⁰+p_n¹+p_n²+...p_n^k_n)

很容易可以想到，每一项 p_i^k_i 都有 k_i+1 个因子，即 p_i⁰ 、p_i¹ 、p_i²  ... p_i^k_i  ，所以 p_i^k_i 的因子和就是 p₁⁰+p₁¹+p₁²+...p₁^k₁ 。（不难看出，这是一个等比数列。）现在要求A的因子和，因为A是 p_i^k_i 的乘积，所以只要把每一项 p_i^k_i 的因子和都相乘就可以了。（这是我的理解，想看更严密的证明可以百度一下）

 

快速幂运算

快速幂也是很基础的一个点了，刚好前段时间也写了随笔，可以戳这里！

代码在这里：

//快速幂运算
long long quickPow(long long a,long long n){
    long long res = 1;
    while(n){
        if(n & 1)
            res = res * a % MOD;
        a =  a * a % MOD;
        n >>= 1;
    }
    return res;
}

 

 

等比数列二分求和

这个大概是这道题的核心了！从上面给出的约数和定理，我们发现A的所有因子之和是等比数列和的乘积。因为一般的等比数列求和公式中有除法，所以求和时不能直接用公式。据说本题有三种做法，二分，逆元，变换取模。本渣渣现在只会第一种，所以先介绍一下二分求和的方法~

观察等比数列的式子 a + a² + ... + aⁿ ，我们发现：

（1）时，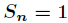

（2） n 为偶数时，

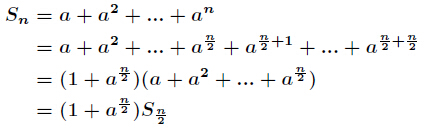
（3） n 为奇数时，

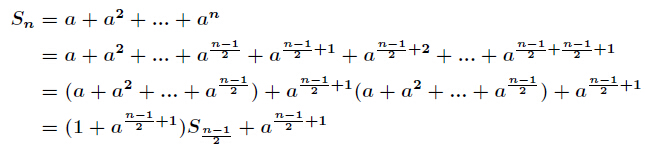
这边我们用到的式子还要再加上1，公式同样也可以像上面这样推出来：

n为奇数，S_n = （1 + a^n/2+1) * S_n/2 ；

n为偶数，Sn = （1 + a^n/2+1)S_n/2-1 + a^n/2 ；

 下面给出代码：

//等比数列二分求和
long long sum(long long p,long long n){  //计算1+p+p^2+...+p^n
    if(p == 0) return 0;
    if(n == 0) return 1;
    if(n & 1)
        return ((1 + quickPow(p,n/2+1)) * sum(p,n/2)) % MOD;
    else
        return ((1+quickPow(p,n/2+1)) * sum(p,n/2-1) + quickPow(p,n/2)) % MOD;

}

 

 

最后！

下面就可以开始写main函数啦，注意注意，一定要小心取模，本渣渣在这边wa了n次，最后才找到问题。话不多说，上代码：

int main(){
    long long A,B;
    getPrime();   //得到素数表
    while(cin>>A>>B){
        getFactors(A);  //分解质因子
        long long ans = 1;
        for(int i = 0; i < cnt; i++){
            ans = ans * sum(p[i],k[i]*B) % MOD; 
        }
        cout<<ans<<endl;
    }

    return 0;
}

筒子萌！！有没有看到那个for循环！！有没有看到里面的 ans = ans * sum(p[i],k[i]*B) % MOD; 这句！

我之前写的是：ans *= sum(p[i],k[i]*B) % MOD; 然后在for循环外面又写了个 ans %= MOD; 自以为万无一失了，然后。。我真的查了很久的错QAQ。。疯狂wa，内心是崩溃的！

注意在取模运算啥的时候能不写这种 *= 、+= 咱就别写啊，真的挺坑的（大佬请自动忽视我这句话），我前面随处都在留意着取模，没想到这边疏忽了，功亏一篑啊。

下面是完整的代码，有兴趣的可以参考一下，另附我参考的几个题解（题解一    题解二）和POJ讨论区的一些测试数据：

#include <iostream>
#include <cstring>
using namespace std;

#define MOD 9901

// 求A^B的所有约数之和%9901

//埃氏筛法筛素
const int MAX_N = 10005;
int prime[MAX_N];
bool is_prime[MAX_N];
void getPrime(){
    int p = 0;
    for(int i = 2; i < MAX_N; i++) is_prime[i] = true;
    for(int i = 2; i < MAX_N; i++){
        if(is_prime[i]){
            prime[p++] = i;
            for(int j = 2*i; j < MAX_N ; j+=i) is_prime[j] = false;
        }
    }
}


//素因子分解 A = p1^k1 * p2^k2 * ... * pn^kn
int p[MAX_N],k[MAX_N];
int cnt;
void getFactors(long long x){
    memset(k,0,sizeof(k));
    cnt = 0;
    for(int i = 0; prime[i]*prime[i] <=x ; i++){
        if(x % prime[i] == 0){  //如果x能被当前素数整除
            p[cnt] = prime[i];
            while(x % prime[i] == 0){
                k[cnt]++;
                x /= prime[i];
            }
            cnt++;
        }
    }
    if(x != 1){   //如果x不为1，剩下的一定是大于等于√x的一个素因子
        p[cnt] = x;
        k[cnt++] = 1;
    }
}

//带模快速幂运算
long long quickPow(long long a,long long n){
    long long res = 1;
    while(n){
        if(n & 1)
            res = res * a % MOD;
        a =  a * a % MOD;
        n >>= 1;
    }
    return res;
}

//等比数列二分求和
long long sum(long long p,long long n){  //计算1+p+p^2+...+p^n
    if(p == 0) return 0;
    if(n == 0) return 1;
    if(n & 1)
        return ((1 + quickPow(p,n/2+1)) * sum(p,n/2)) % MOD;
    else
        return ((1+quickPow(p,n/2+1)) * sum(p,n/2-1) + quickPow(p,n/2)) % MOD;

}

int main(){
    long long A,B;
    getPrime();   //得到素数表
    while(cin>>A>>B){
        getFactors(A);  //分解质因子
        long long ans = 1;
        for(int i = 0; i < cnt; i++){
            ans = ans * sum(p[i],k[i]*B) % MOD;
        }
        cout<<ans<<endl;
    }

    return 0;
}