Python一行流：生成任意长度K-mer序列的集合
太长不看版
reduce(lambda x,y: [i+j for i in x for j in y], [['A','T','C','G']] * K)
K-mer介绍
引用刘尧老师在科学网博文上的介绍：
mer，其在分子生物学领域中意义为单体单元 （monomeric unit，mer）。通常用于核酸序列中的单位，代表nt或者bp，例如，100 mer DNA代表这段DNA序列单链长度100nt，或者双链长度100bp。
而k-mer则是指将核酸序列分成包含k个碱基的字符串，即从一段连续的核酸序列中迭代地选取长度为K个碱基的序列，若核酸序列长度为L，k-mer长度为K，那么可以得到L-K+1个k-mers。如下图所示，假设这里存在某序列长度为21，设定选取的k-mer长度为7，则得到（21-7+1=15）个7-mers。
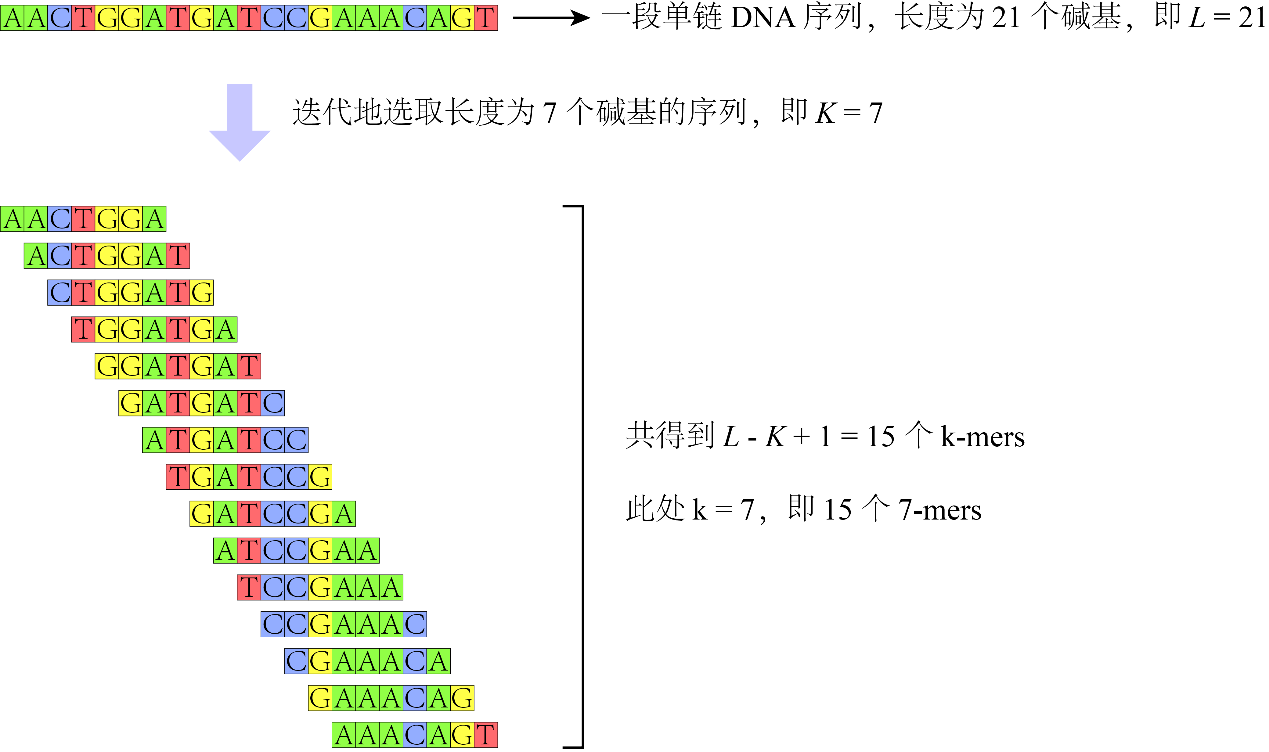
原理
Reduce思想
- Reduce：对于一串序列中的第一和二个元素计算出某个值（自己指定算法），用该计算结果与第三个元素计算，再用该计算结果与第四个元素进行计算……
- 比如计算阶乘
50!，可以用reduce( lambda x, y: x * y, range(1, 50) )。range(1, 50)是从1到50的序列，这里lambda函数是将传入的两个数相乘。应用reduce之后就变成了：res= 1 * 2res= res * 3res= res * 4- ……
res = res * 50
- 实际相当于
1 * 2 * 3 * 4 * ...... * 50 = 50!
算法原理
此处我们应用reduce的思想，将构建K-mer组合的过程想象成对于K列由[A, C, G, T]组成的碱基矩阵，进行reduce操作：每次都返回序列和碱基的所有拼接组合，如对于[A, C, G, T]和[A, C, G, T]，就会组合成一个K为2、长度为\(4^2\)的K-mer集合[AA, AC, AG, AT, CA, CC, ...... TG, TT]。
构造所有的8-mer序列组成集合的过程，用图形来表示就是：
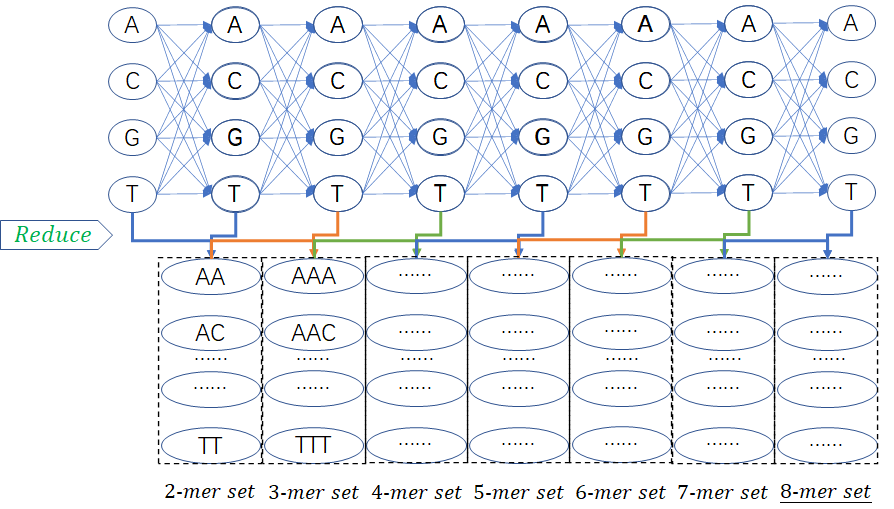
神似神经网络中的 Fully Connected layer？
常规实现
使用for...in...循环，代码结构比较复杂，行数多，函数要起名。因为这个K-mer集合生成算法和神经网络中的全连接层之间的传播过程类似，所以用了concate_fullconnect这个名字，写法如下：
from functools import reduce
K = 3
def concate_fullconnect(mer_set, bases):
res = []
for i in mer_set:
for j in bases:
res.append(i+j)
return res
reduce(concate_fullconnect, [['A','T','C','G']] * K)
一行流
介绍
用列表推导式、lambda、map、reduce、filter等等函数代替多行的for...in...循环，实现代码结构的简化。
特点
- 代码行数缩短，一行代码做一件事，逻辑更清晰；
map、reduce和推导式等的易读性稍弱于for...in...循环，但for...in...在嵌套过多时可读性非常差；- 执行效率更高，因为map、reduce、filter和推导式都是优化过了的，比直接循环效率高30%左右（后续有验证）。
一行流实现
使用如下的代码生成任意长度的所有K-mer序列组合
reduce(lambda x,y: [i+j for i in x for j in y], [['A','T','C','G']] * K)
[['A','T','C','G']] * K是长度为K、宽度为4的碱基矩阵[i+j for i in x for j in y]是Python列表推导式- 推导式放在
lambda中组成了一个匿名函数 - 最后使用
reduce将函数应用在碱基矩阵上就能够得到所有K-mer序列组合。
需要额外注意的是，在Python3中reduce函数被放在了functools模块里，需要导入才能使用，所以实际使用是这样的：
from functools import reduce
K = 3
reduce(lambda x,y: [i+j for i in x for j in y], [['A','T','C','G']] * K)
性能对比
- 计算长度为3的所有K-mer组合，使用Ipython console和
timeit模块进行运行时间统计。可以看到一行流写法快了接近5秒。
- 计算长度为4的所有K-mer组合，一行流快了25秒。
代码如下：
timeit('''from functools import reduce
K = 3
def concate_fullconnect(mer_set, bases):
res = []
for i in mer_set:
for j in bases:
res.append(i+j)
return res
reduce(concate_fullconnect, [['A','T','C','G']] * K)''')
timeit("from functools import reduce; reduce(lambda x,y: [i+j for i in x for j in y], [['A','T','C','G']]*3)")
- 如果你想了解推导式、reduce和lambda，推荐你阅读Interpy
