交错字符串

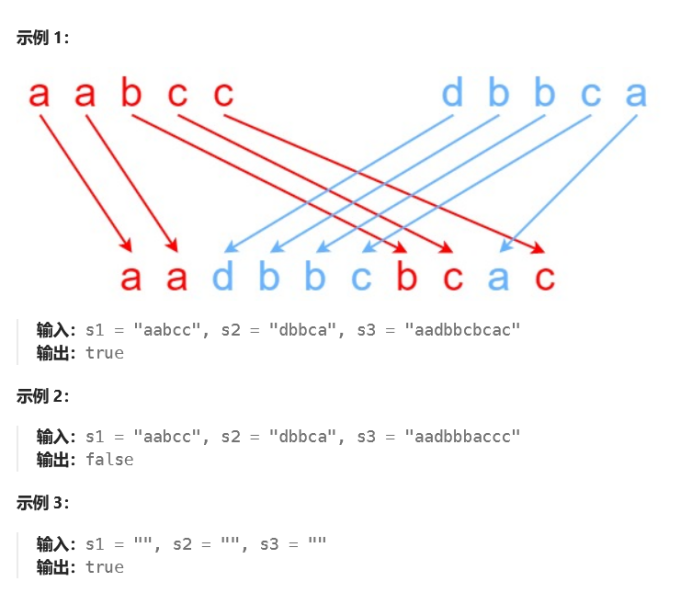
给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。

两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空 子字符串：

• s = s₁ + s₂ + ... + s_n
• t = t₁ + t₂ + ... + t_m
• |n - m| <= 1
• 交错 是 s₁ + t₁ + s₂ + t₂ + s₃ + t₃ + ... 或者 t₁ + s₁ + t₂ + s₂ + t₃ + s₃ + ...

注意：a + b 意味着字符串 a 和 b 连接。

思路

假设s3是由s1跟s2字符串拼接组成，那么

1、s3的最后一个字符一定是s1的最后一个字符或者s2的最后一个字符

2、且去掉最后一个字符后，上述1仍然成立

因此问题含有重复子结构，且含有最优解，考虑使用动态规划

1、定义最优解dp[i][j]:表示si跟sj是否可以交错分割组成s（i+j）

2、定义状态转移方程：

　　s（i+j）= (dp[i - 1][j] && s1.charAt(i - 1) == s3.charAt(i+j - 1)) || (dp[i][j - 1] && s2.charAt(j - 1) == s3.charAt(i+j - 1))

3、初始化dp[0][0]为true，表示空字符串是支持的

代码

class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        if (s1.isEmpty()){
            return s2.equals(s3);
        }
        if (s2.isEmpty()){
            return s1.equals(s3);
        }
        if (s1.length() + s2.length() != s3.length()){
            return false;
        }

        boolean[][] dp = new boolean[s1.length() + 1][s2.length() + 1];
        dp[0][0] = true;


        for (int i = 0; i <= s1.length(); i++) {
            for (int j = 0; j <= s2.length(); j++) {
                if (dp[i][j]){
                    continue;
                }
                if (i - 1 >= 0){
                    dp[i][j] = dp[i][j] || (dp[i - 1][j] && s1.charAt(i -1) == s3.charAt(i + j -1));
                }
                if (j - 1 >= 0){
                    dp[i][j] = dp[i][j] || (dp[i][j - 1] && s2.charAt(j - 1) == s3.charAt(i + j - 1));
                }
            }
        }
        return dp[s1.length()][s2.length()];
    }
}