最长公共子序列-套路级理解

题目：给定两个字符串 str1 和 str2，返回这两个字符串的最长公共子序列的长度
解释：一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串，如下图示：

 

 

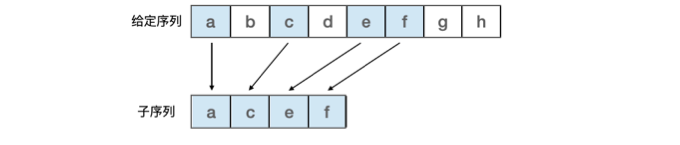
也就是说对于以下两个字符串 str1 和 str2，其最长公共子串为 「acg」。

 

 

动规套路

动态规划,简而言之就是求状态转移方程,然后根据方程自下而上地求出原问题的解.

总结了以下套路:

1、判断是否是动态规划

• 找最优子结构
  • 　　最优子结构:也就是说我们的问题可以分为N个子问题,每个子问题都有一个最优解,而最终解依赖于每个最优解的组合

• • 　　比如说:str1和str2的最优子结构是依赖于str1-1,str2-1

• 找重叠子问题
  • 　　也就是说大问题的解依赖于子问题的最优解的组合.
  • 比如说:str1和str2的最优子结构是依赖于str1-1,str2-1,而str1-1,str2-1依赖于str1-2,str2-2....

2、使用数组表示题目的含义

既然是两个字符串的公共子序列那么应该使用二维数组来表示.

• dp 是个二维数组，即 dp[i][j], 表示对于子串 str1[0..i] 与子串 str2[0..j], 它们的最长公共子序列长度为 dp[i][j]，这样的话根据定义， dp[str1.length-1][str2.length-1] 即为所求的解。

3、找状态转移方程

• 画dpTable,观察规律

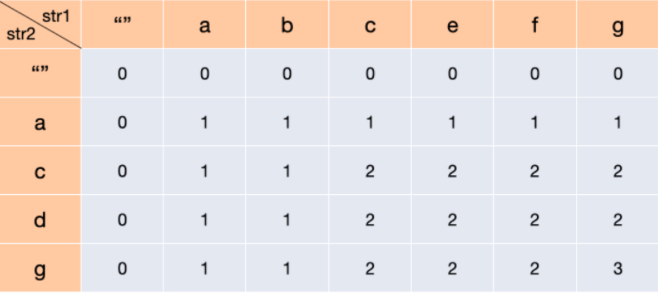
• 求状态转移方程
  • 当两个字符串 i，j 索引对应的字符相等时
    • 显然 dp[i][j] = dp[i-1][j-1] +1, 1 代表 i 和 j 指向的字符相等，dp[i-1][j-1] 代表除此相同字符外的 i，j 索引之前字符串的公共子序列。
  • 　　　　当两个字符串 i，j 索引对应的字符不相等时
    • 　　　　　　此时 dp[i][j] 值可能为 dp[i-1][j] 或 dp[i][j-1]， dp[i-1][j] 怎么理解，既然 i 与 j 指向的字符不等，那只要丢弃 i 字符，求 str1[0..i-1] 与 str2[0..j] 的最长公共子序列即可，即 dp[i-1][j], 同理对于dp[i][j-1]，即为丢弃 j ，求 str1[0..i] 与 str2[0..j-1] 的最长公共子序列
  • 　　既然 dp[i][j] 有可能等于这两个值，那么显然应该取这两者的较大值， 

    即 dp[i][j] = max(dp[i-1][j], dp[i][j-1])。因此状态转移方程为:　

4、找basecase

• 也就是找到数组的初始值,然后自下而上的求解我们的问题
• 因为我们不能确定初始值是否一定相等,所以我们可以把第一个字符设为空字符串“”,这样我们的第一个字符的最长子序列一定为0,也就找到了我们的初始值.

小结

状态转移方程的规律总是要去找dp[i][j]与dp[i-1][j-1],dp[i-1][j],dp[i][j-1]三者之间的关系的.

另外想清楚dp[i][j]代表的含义很容易理清我们的思路,而含义往往根据我们的题目要求自行理解.

代码

public class Soultion {
    public static int maxSubSequ(char[] str1, char[] str2) {
        int[][] dp = new int[str1.length][str2.length];
        for (int i = 1; i < str1.length; i++) {
            for (int j = 1; j < str2.length; j++) {
                if (str1[i] == str2[j]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[str1.length - 1][str2.length - 1];
    }

    public static void main(String[] args) {
        char[] x = {' ', 'a', 'b', 'c', 'e', 'f', 'g'};
        char[] y = {' ', 'a', 'c', 'd', 'g'};
        int maxSubSequ = maxSubSequ(x, y);
        System.out.printf("maxSubSequ = " + maxSubSequ);
    }
}