数组

一、二分查找

必要条件：递增有序数组、无重复元素
包括两种边界条件[ ]和[ )，决定到底是 while(left < right) 还是 while(left <= right)
while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
收缩边界 if (nums[middle] > target) 则right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1
>>右移符号相当于除以2

  class Solution {
  public:
      int search(vector<int>& nums, int target) {
          int left = 0;
          int right = nums.size()-1;
          while (left <= right){
              int middle = left + ((right - left) >> 1);
              if (nums[middle] > target)
                   right = middle-1;
              else if (nums[middle] < target)
                  left = middle+1;
              else
                  return middle;
          }
          return -1;
      }
  };

二、移除元素

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。示例 1: 给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。示例 2: 给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。

时间复杂度：时间复杂度的排序：由小到大依次为： O（1）< O(log n) < O(n) < O(nlog n) < O(n^2) ...<O(2^n) < O(n!)
暴力解法,解法就是两层for循环，一个for循环遍历数组元素，第二个for循环更新数组。

// 时间复杂度：O(n^2)
// 空间复杂度：O(1)
class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int size = nums.size();
        for (int i = 0; i < size; i++) {
            if (nums[i] == val) { // 发现需要移除的元素，就将数组集体向前移动一位
                for (int j = i + 1; j < size; j++) {
                    nums[j - 1] = nums[j];
                }
        //不需要      i--; // 因为下表i以后的数值都向前移动了一位，所以i也向前移动一位
                size--; // 此时数组的大小-1
            }
        }
        return size;

    }
};

双指针法（快慢指针法）：通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。双指针法（快慢指针法）在数组和链表的操作中是非常常见的，很多考察数组、链表、字符串等操作的面试题，都使用双指针法。

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex <nums.size(); fastIndex++ ){
            if (nums[fastIndex] != val){
                nums[slowIndex] = nums[fastIndex];
                slowIndex ++;
            }
        }
        return slowIndex;
    }
};

三、有序数组的平方

给你一个按非递减顺序排序的整数数组 nums，返回每个数字的平方组成的新数组，要求也按非递减顺序排序。

sort(nums.begin(),nums.end())时间复杂度nlog n;
先平方再排序
双指针法:两个指针，一个指向数组头，一个指向尾

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        int k = nums.size() - 1;
        vector<int> result(nums.size());
        for (int i = 0, j = nums.size() - 1; i<=j;){
            if (nums[i]*nums[i] < nums[j]*nums[j] ){
                result[k--] = nums[j] * nums[j];
                j--;
            }
            else{
                result[k--] = nums[i]*nums[i];
                i++;                
            }
        }
        return result;
    }
};

四、长度最小子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其和 ≥ target 的长度最小的连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

暴力解决：两个for循环遍历，一个指向起始位置，另一个做加法；时间复杂度O（n^2）
双指针法：滑动窗口法时间复杂度O（n）.所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX;
        int sum = 0; // 滑动窗口数值之和
        int i = 0; // 滑动窗口起始位置
        int subLength = 0; // 滑动窗口的长度
        for (int j = 0; j < nums.size(); j++) {
            sum += nums[j];
            // 注意这里使用while，每次更新 i（起始位置），并不断比较子序列是否符合条件
            while (sum >= s) {
                subLength = (j - i + 1); // 取子序列的长度
                result = result < subLength ? result : subLength;
                sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处，不断变更i（子序列的起始位置）
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

五、螺旋矩阵

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

思路
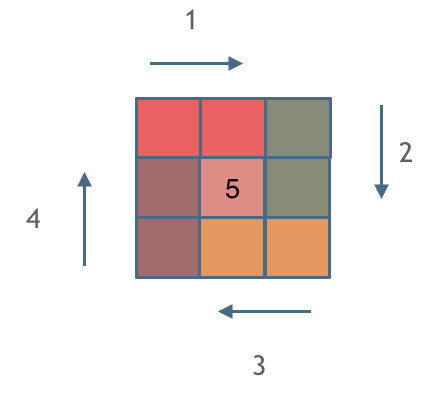
模拟顺时针画矩阵的过程:

填充上行从左到右
填充右列从上到下
填充下行从右到左
填充左列从下到上

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> res(n, vector<int>(n, 0)); // 使用vector定义一个二维数组
        int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
        int loop = n / 2; // 每个圈循环几次，例如n为奇数3，那么loop = 1 只是循环一圈，矩阵中间的值需要单独处理
        int mid = n / 2; // 矩阵中间的位置，例如：n为3， 中间的位置就是(1，1)，n为5，中间位置为(2, 2)
        int count = 1; // 用来给矩阵中每一个空格赋值
        int offset = 1; // 每一圈循环，需要控制每一条边遍历的长度
        int i,j;
        while (loop --) {
            i = startx;
            j = starty;

            // 下面开始的四个for就是模拟转了一圈
            // 模拟填充上行从左到右(左闭右开)
            for (j = starty; j < starty + n - offset; j++) {
                res[startx][j] = count++;
            }
            // 模拟填充右列从上到下(左闭右开)
            for (i = startx; i < startx + n - offset; i++) {
                res[i][j] = count++;
            }
            // 模拟填充下行从右到左(左闭右开)
            for (; j > starty; j--) {
                res[i][j] = count++;
            }
            // 模拟填充左列从下到上(左闭右开)
            for (; i > startx; i--) {
                res[i][j] = count++;
            }

            // 第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
            startx++;
            starty++;

            // offset 控制每一圈里每一条边遍历的长度
            offset += 2;
        }

        // 如果n为奇数的话，需要单独给矩阵最中间的位置赋值
        if (n % 2) {
            res[mid][mid] = count;
        }
        return res;
    }
};

posted @ 2021-10-06 11:09 Ada_CN 阅读(43) 评论(0) 编辑收藏举报

刷新页面返回顶部

Ada_CN

数组

一、二分查找

二、移除元素

三、有序数组的平方

四、长度最小子数组

五、螺旋矩阵

公告