堆排序(Heap Sort)

介绍：

　　顾名思义，堆排序就是利用堆(Heap)这种数据结构进行排序，在堆排序算法中，我们使用的是最大堆(大根堆)，堆排序是一种选择排序。

算法描述：

　　第一步：利用build_max_heap函数将输入数据构建大根堆。

　　第二步：因为大根堆中的最大元素总是在根节点，通过把它与堆的最后一个元素交换，就可以把该元素放在正确的位置(从此可以看出堆排序是一种选择排序)。

　　第三步：从堆中去掉最后一个元素，剩余结点中，原来根的孩子结点仍然是大根堆，而新的根结点可能会违背最大堆性质，因此，我们需要调用max_heapify函数维护最大堆性质。

　　第四步：重复上述过程，直到堆的大小减小到1；

图片演示：

 

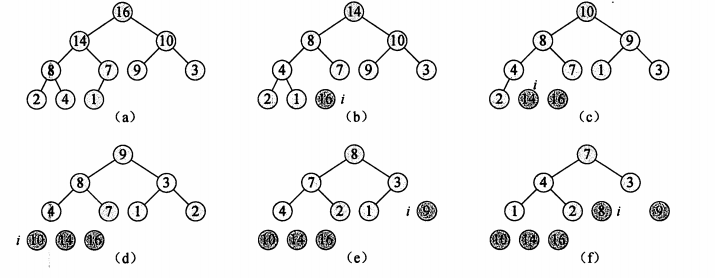
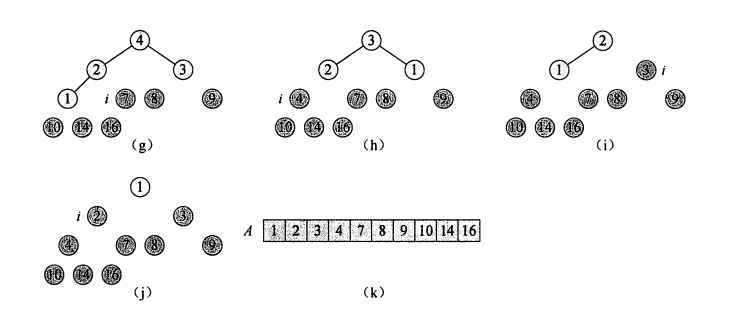
动图演示：

 　　　　　　　　　　　　　　　　　　　　　动图来源：www.runoob.com

 性能分析：

　　时间复杂度：O(NlogN)　　

   空间复杂度：O(1)

   稳定性：不稳定

代码实现：

// 堆排序(C++)
void heap_sort(int a[], int length) {
    build_max_heap(a, length);// 建大根堆
    
    // 每次将最大元素放在正确位置
    for (int i = length - 1; i > 0; --i) {
        int tmp = a[i];// 交换堆根与堆最后一个元素
        a[i] = a[0];
        a[0] = tmp;
        max_heapify(a, i, 0);// 维护大根堆性质
    }
}
// 维护大根堆性质
void max_heapify(int a[], int length, int i) {
    int left = 2 * i;// 左孩子位置
    int right = left + 1;// 右孩子位置
    int largeindex = i;// 记录当前结点与左孩子右孩子中最大
    
    // 判断左孩子是否大于当前结点
    if (left < length && a[left] > a[largeindex]) {
        largeindex = left;
    }
    // 判断右孩子是否大于当前最大结点
    if (right < length && a[right] > a[largeindex]) {
        largeindex = right;
    }
    // 判断是否已经不需维护
    if (largeindex != i) {
        int tmp = a[i];// 交换
        a[i] = a[largeindex];
        a[largeindex] = tmp;
        // 由于以该结点为根的子树有可能违反大根堆性质
        // 因此递归调用max_heapify
        max_heapify(a, length, largeindex);
    }
}
// 建堆
void build_max_heap(int a[], int length) {
    // 对length / 2到0维护大根堆性质
    for (int i = length / 2; i >= 0; --i) {
        max_heapify(a, length, i);
    }
}

参考书籍：《算法导论》