排序算法-------堆排序

对于n个元素的序列{R0, R1, ... , Rn}当且仅当满足下列关系之一时，称之为堆：

(1) Ri <= R2i+1 且 Ri <= R2i+2 (小顶堆)

(2) Ri >= R2i+1 且 Ri >= R2i+2 (大顶堆)

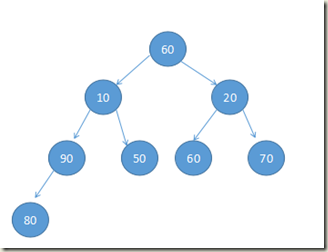
堆其实是一个顺序存储的完全二叉树

               完全二叉树：

               顺序存储：

 

              大顶堆：

                              

堆排序：

利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。

    其基本思想为(大顶堆)：

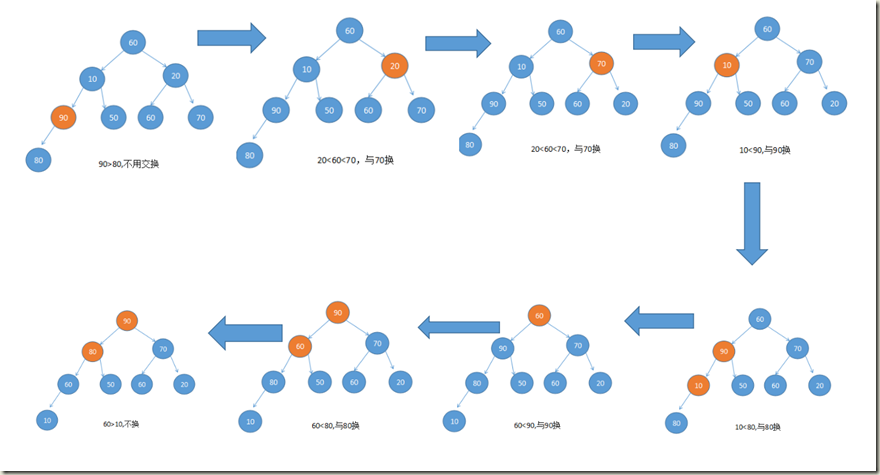
    1)将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆，此堆为初始的无须区；

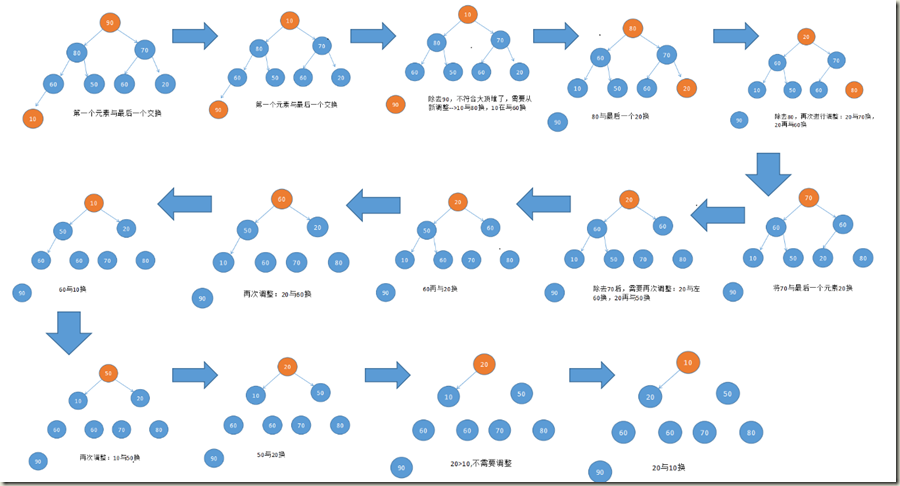
    2)将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n];

    3)由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

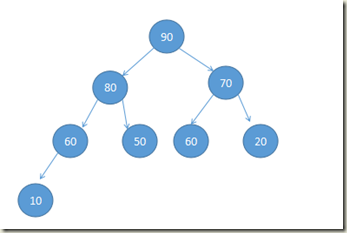
第一步如何将一个数组初始化成大顶堆：

如何排序呢？

经过排序后，数组就会变得有序

 

 

package com.neuedu.java;

import java.util.Arrays;

/**
 * 堆排序
 * @author wzc
 */
public class HeapSort {
     public static void main(String[] args) {
         int []a={60,50,30,90,80,20,10,50,40};
         //调用堆排序方法
         heapSort(a);
         //输出数组
         System.out.println(Arrays.toString(a));
    }
     
     /**
      * 堆排序方法
      * @param a   待排序数组
      */
     public  static void heapSort(int [] a){
          int end=a.length-1;   //end为数组最后一个数下标
          //初始化堆---->大顶堆
          for(int i=(end-1)/2;i>=0;i--){ //从第一个有孩子节点的节点开始
              //进行堆调整--->大顶堆
              headAdjuest(a, i, end);
              
          }
          //进行排序
          for(int j=end;j>0;j--){
              //1.第一个数与最后一个数进行交换
              int temp=a[0];
              a[0]=a[j];
              a[j]=temp;
              
              //2.交换后，再次进行堆调整--->大顶堆
              headAdjuest(a, 0, j-1);
          }
     }
     /**
      * 进行堆调整的方法
      * @param a    待调整的数组
      * @param parent   当前父节点下标
      * @param end      数组最后一个数的下标
      */
     public static void  headAdjuest(int [] a,int parent,int end){
         int temp =a[parent];   //存储一下当前父节点---便于后续比较和数据交换
         int child =2*parent+1;  //获取当前父节点的左孩子下标
         System.out.println(temp);
         //判断左孩子是否存在
         while(child<=end){
             if ((child+1)<=end&&a[child]<a[child+1]) {
                child++;         //判断右孩子是否存在，找到孩子节点中最大的那个
            }
             //如果父节点比孩子节点都大，那就没必要调整了，直接退出
            if (temp>=a[child]) { 
                break;
            }
            
            a[parent]=a[child];   //将孩子中最大的那个交给父节点
            parent=child;         //如果child节点也是个父节点，为了保证child节点交换后的数据比child自己孩子节点数据都大，
                                  //还要在进行循环，此时child节点有为父节点，和他自己的孩子节点在进行比较
            child=2*child+1;
         }
         a[parent]=temp;           //完成数据交换
     }
         
}