大话数据结构----栈
栈的定义:
栈(stack)是限定尽在表尾进行插入和删除操作的线性表。
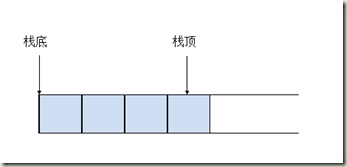
从定义中可以看出,栈也是线性表,是一个特殊的线性表,之前说线性的表的时候,线性表可以在任意位置进行插入插入,而栈比线性表特殊的地方的就是不能随意的插入和删除了,栈的插入和删除只能在规定的同一端进行,而被允许插入和删除的一端称为栈顶,另一端称为栈底。
从栈的特性中我们能发现:1).栈是一种后进先出的线性表,因为栈只有一个出入口,每次出栈是最后进的那个先出去,后一个才能出去,就像我们出电梯一样,里面的人被阻住,只有外面的人出去,里面的人才能出去。
2)栈的栈顶是在变化的,所以栈还得有一个栈顶指针,新元素入栈的后,栈顶指针要指向新栈顶,栈顶栈顶元素出栈时,栈顶指针也是需要变化指向新的栈顶
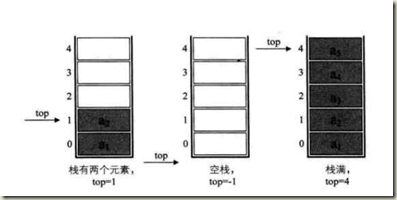
栈的 三种状态-----栈空、栈满、栈未满
栈空时:栈顶指针(top)=-1
栈满时:栈顶指针(top)=MAXSIZE-1;
栈未满:就是占中存在元素,top指针还未达到MAXSIZE-1.
进栈和出栈操作
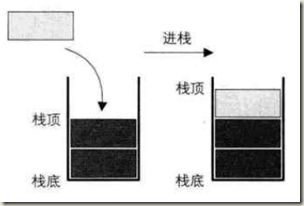
进栈
1).判断栈是否已经满了,如果满了当然就入不了栈。
2)、栈顶指针+1,在新栈顶位置存入要进栈的元素。
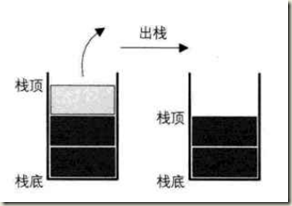
出栈:
1).判断栈是否为空,里面没有数据先出栈也没有。
2).将栈顶元素出栈,栈顶指针-1.
Java 实现栈的基本操作
package JavaStack; import javax.swing.table.TableColumn; /* * 项目名称:JavaStack * @author:wzc * @date 创建时间:2017年9月10日 下午2:22:08 * @Description:数据结构----栈 * @parameter * */ public class Stack<T> { public static final int MAXSIZE=10; private static final int T = 0; private T [] date=(T[])new Object[MAXSIZE]; int top; public Stack() { top=-1; } //判断栈是否为空 public boolean isEmpty(){ if (top==-1) { return true; } return false; } //判断栈是否满 public boolean isFull(){ if (top==MAXSIZE-1) { return true; } return false; } /*Method:push *Description:入栈操作 *param:T date 入栈的数据元素 */ public void push(T date){ //1.入栈之前判断是否栈满 if (isFull()) { System.out.println("栈已经满了"); return; } top=top+1; this.date[top]=date; System.out.println(date+"已经入栈"); } /*Method:enclosing_method *Description:出栈操作 *param: */ public T pop(){ //出栈之前判断呢栈是否为空 if (isEmpty()) { System.out.println("栈为空,无可出栈数据"); return null; } T date= this.date[top]; top=top-1; return date; } //输出栈 中有多少元素 public int getLength(){ return top+1; } //输出栈中所有元素 public void getDate(){ for(int i=0;i<=top;i++){ System.out.print(date[i]+" "); } System.out.println(); } }
测试一下:
@Test public void test() { Stack <Integer> stack=new Stack<>(); int length = stack.getLength(); System.out.println("栈长:"+length); stack.push(2); System.out.println("栈长"+stack.getLength()); stack.push(5); stack.push(9); System.out.println("栈长"+stack.getLength()); stack.getDate(); Integer pop = stack.pop(); System.out.println(pop+"出栈"); System.out.println("栈长"+stack.getLength()); stack.getDate(); stack.pop(); stack.pop(); System.out.println("栈长"+stack.getLength()); stack.getDate(); stack.pop(); }
测试结果::
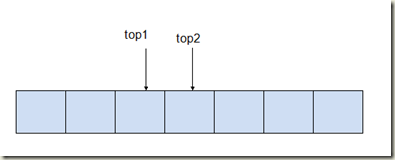
共享栈
共享栈 是开辟一块内存空间,两个栈结构共用这一块内存空间,每个栈占领这块空间的一头。
要求:两个栈的数据类型要相同。
栈满:判断栈满的条件是----top1+1=top2
栈空: 1.第一个栈空的条件:top=-1
2.第二个栈空的 条件:top2=MAXSIZE
在两个栈对于空间需求相反的时候,利用共享栈可以有效的节约空间。
package JavaStack; /* * 项目名称:JavaStack * @author:wzc * @date 创建时间:2017年9月10日 下午3:07:28 * @Description:共享栈 * @parameter * */ public class DoubleStack<T> { public static final int MAXSIZE=10; private T [] date=(T[])new Object[MAXSIZE]; int top1; int top2; public DoubleStack() { top1=-1; top2=MAXSIZE; } //判断栈1是否为空 public boolean isEmpty1(){ if (top1==-1) { return true; } return false; } //判断栈2是否为空 public boolean isEmpty2(){ if (top2==MAXSIZE) { return true; } return false; } //判断栈是否满 public boolean isFull(){ if (top1+1==top2) { return true; } return false; } /*Method:push *Description:入栈操作 *param:T date 入栈的数据元素,StackNum 哪个栈 */ public void push(T date,int StackNum){ //1.入栈之前判断是否栈满 if (isFull()) { System.out.println("栈已经满了"); return; } if (StackNum==1) { top1=top1+1; this.date[top1]=date; System.out.println(date+"已经入栈"); }else if (StackNum==2) { top2=top2-1; this.date[top2]=date; System.out.println(date+"已经入栈"); } } /*Method:enclosing_method *Description:出栈操作 *param:StackNum ,哪个栈 */ public T pop(int StackNum){ //第一个栈出栈 if (StackNum==1) { //出栈之前判断呢栈是否为空 if (isEmpty1()) { System.out.println("栈为空,无可出栈数据"); return null; } T date= this.date[top1]; top1=top1-1; return date; }else if (StackNum==2) {//第二个栈出栈 //出栈之前判断呢栈是否为空 if (isEmpty2()) { System.out.println("栈为空,无可出栈数据"); return null; } T date= this.date[top2]; top2=top2+1; return date; } //栈错误 return null; } }
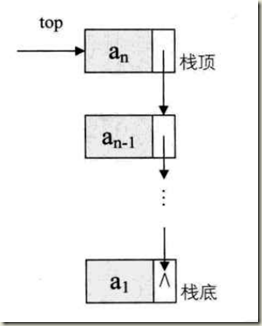
栈的链式存储结构
利用单链表的思想,栈中元素在内存中的存储位置是随机的,只需要它的前驱能找到就行,然后对数据的操作仍然是从栈顶操作,依旧是后进先出。
对于进栈、出栈的实现思想还是一样。
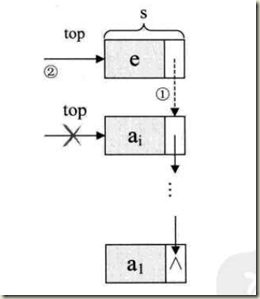
入栈:
1.入栈元素的指针域指向当前栈顶指针top指向的元素。
2.top指针+1,指向新的栈顶元素。
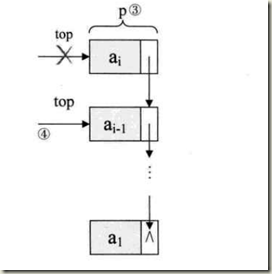
出栈
1.将出栈元素出栈;
2.将top指针-1,指向下一个元素;
package JavaStack; /* * 项目名称:JavaStack * @author:wzc * @date 创建时间:2017年9月10日 下午3:26:54 * @Description:链式存储栈结构 * @parameter * */ public class LinkStack <T>{ private class StackNode{ T date; StackNode next; } private StackNode top; private int count; public LinkStack() { count =0; top=null; } //判读是否为空 public boolean isEmpty(){ if (count==0) { return true; } return false; } /*Method:push *Description:入栈操作 *param:date 入栈元素 */ public void push(T date){ StackNode newNode=new StackNode(); newNode.date=date; newNode.next=top; top=newNode; count++; System.out.println(date+"入栈"); } /*Method:pop *Description:出栈操作 *param: */ public T pop(){ if (isEmpty()) { return null; } StackNode date=top; top=top.next; date.next=null; System.out.println(date.date+"出栈"); return date.date; } public void getDate(){ StackNode tmp=top; while(tmp!=null){ System.out.print(tmp.date+" "); tmp=tmp.next; } System.out.println(); } }