Prim算法-Python实现

流程图

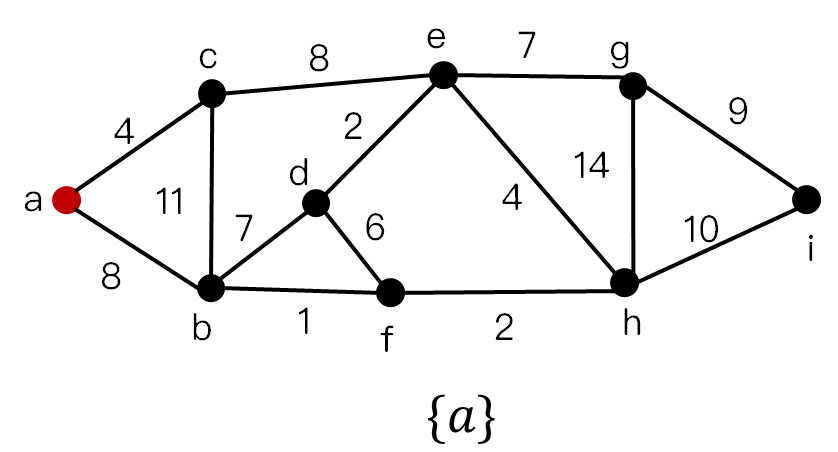
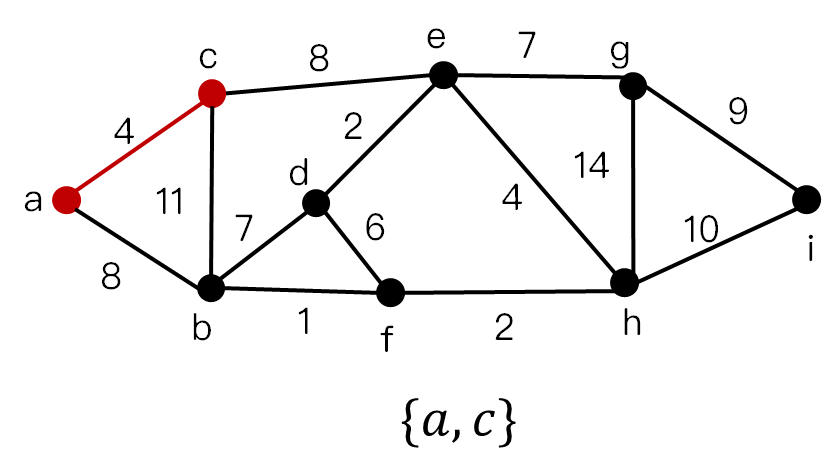
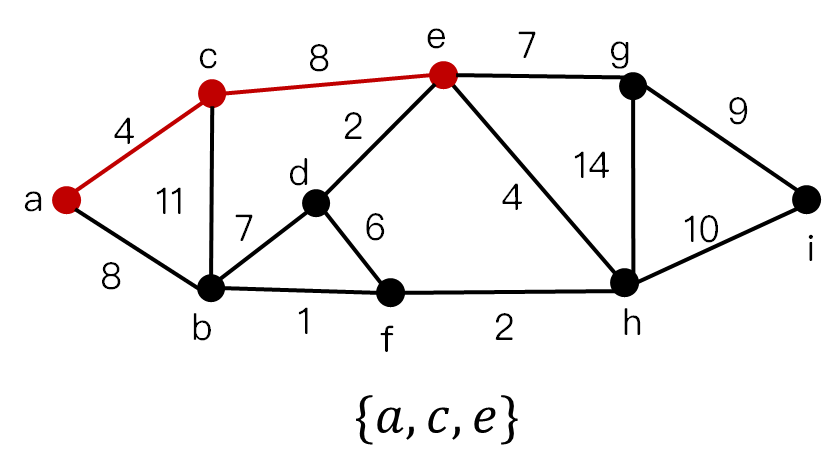
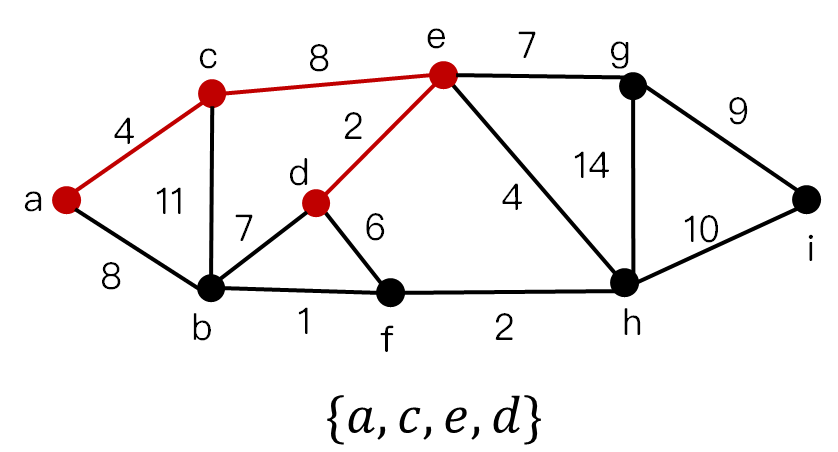
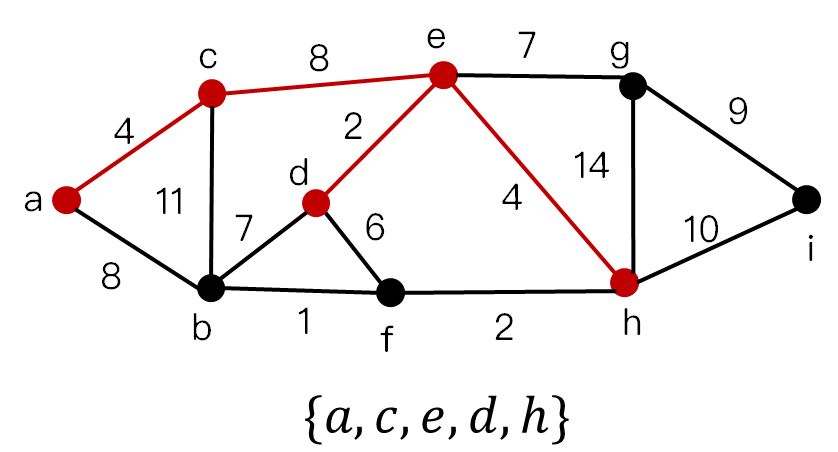
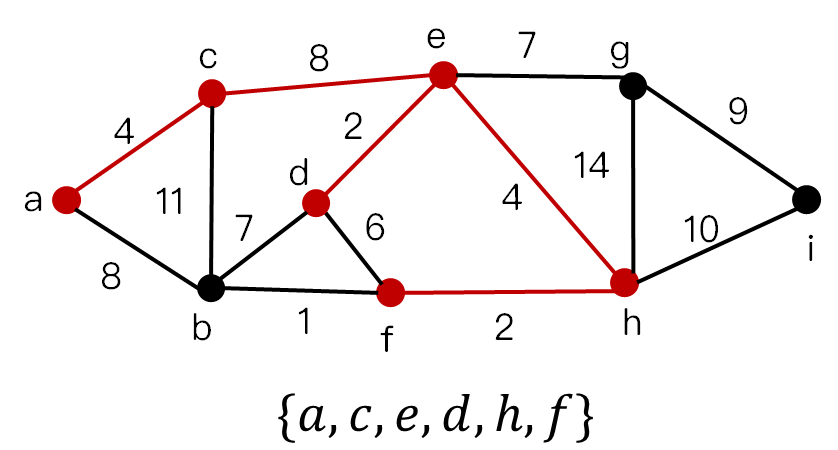
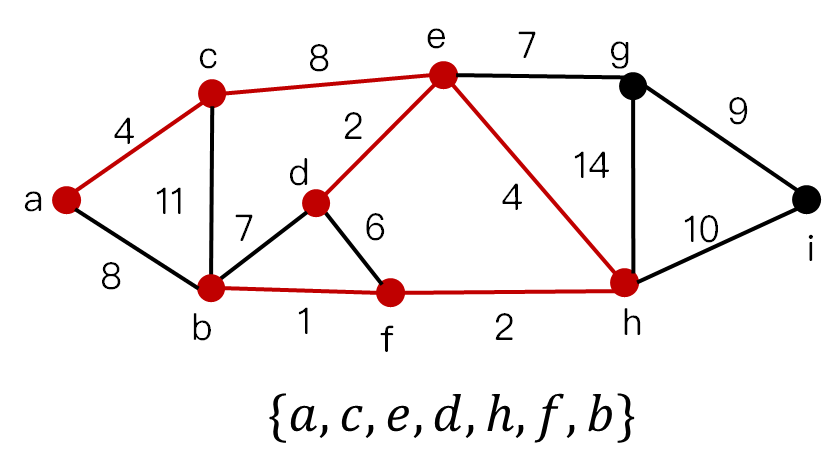
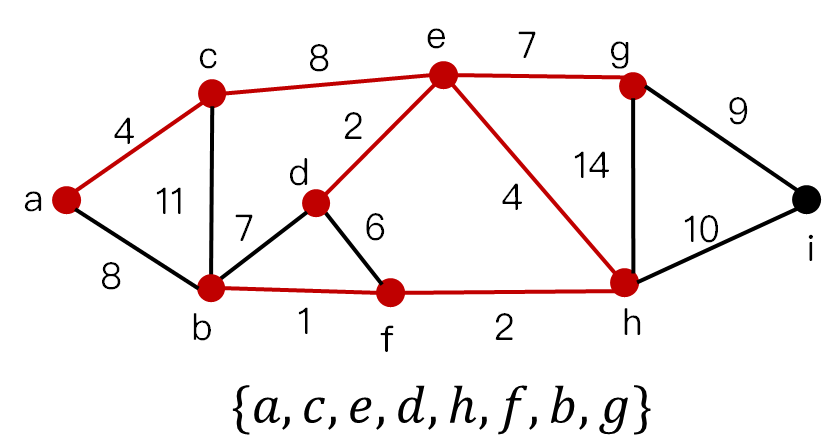
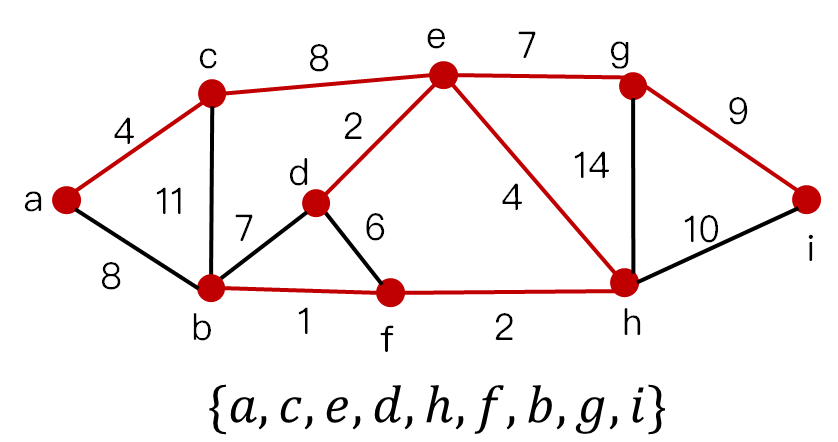
最小生成树

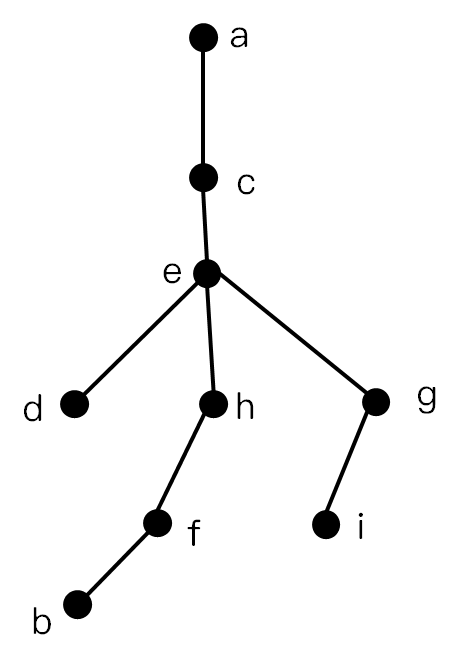
Python 实现

Graph = {
    'a': {
        'b': 8,
        'c': 4,
    },
    'b': {
        'a': 8,
        'c': 11,
        'd': 7,
        'f': 1
    },
    'c': {
        'a': 4,
        'b': 11,
        'e': 8
    },
    'd': {
        'b': 7,
        'e': 2
    },
    'e': {
        'c': 8,
        'd': 2,
        'h': 4,
        'g': 7
    },
    'f': {
        'd': 6,
        'b': 7,
        'h': 2
    },
    'g': {
        'e': 7,
        'h': 14,
        'i': 9
    },
    'h': {
        'e': 4,
        'f': 2,
        'g': 14,
        'i': 10
    },
    'i': {
        'g': 9,
        'h': 10
    }
}


def Prim(Graph, Root):
    # 已经访问的节点
    NodeVisited = []
    # 未访问的节点
    NodeNotVisited = list(Graph.keys())
    # 初始化最小生成树
    Tree = {}
    for item in NodeNotVisited:
        Tree[item] = {}

    # 访问根节点
    NodeVisited.append(Root)  # 将根节点标记为已访问
    NodeNotVisited.remove(Root)  # 从未访问列表里删除根节点

    # 当没有未访问的节点时退出循环
    while len(NodeNotVisited):
        ShortDist = 0  # 最小权值(距离)
        TargetNode = ''  # 目标节点
        PrecNode = ''
        # 以已经访问的节点作为起点
        # 获取已经访问过节点的键
        for item in NodeVisited:
            # 遍历访问过的节点的内容
            for (Key, Value) in Graph.get(item).items():
                # 如果不在已经访问过的节点里
                if Key not in NodeVisited:
                    # ShortDist == 0 或者不是最短的时候就修改
                    if ShortDist == 0 or ShortDist >= Value:
                        ShortDist = Value
                        TargetNode = Key
                        PrecNode = item

        # 遍历结束后将最短路径的那个节点加入已经访问节点列表
        NodeVisited.append(TargetNode)
        # 前一个节点和后一个节点互相绑定
        Tree[PrecNode].update({TargetNode: ShortDist})
        Tree[TargetNode].update({PrecNode: ShortDist})
        # 从未访问的节点中删除
        NodeNotVisited.remove(TargetNode)

    return Tree


if __name__ == '__main__':
    print(Prim(Graph, 'a'))

瞎写的，也不知道对不对，百度也查不到 😥
没有讨论特殊情况(因为暂时想不到特殊情况)
欢迎留言讨论 ( •̀ ω •́ )✧