栈
【题目描述】
考虑这样一个问题,有一个1~n的操作数序列,栈的深度大于n。
现在可以进行以下两种操作:
(1)将一个数,从操作数序列的头端移到栈的头端;
(2)将一个数,从栈的头端移到输出序列的尾端;
使用这两种操作,由一个操作数序列就可以得到一系列的输出序列。
现在给定一个n,询问经过操作1~n操作数序列可能得到的输出序列的总数。
【输入描述】
输入一个整数n(1 ≤ n ≤ 18)。
【输出描述】
输出一个数,表示可能的输出序列的总数。
【样例输入】
3
【样例输出】
5
【数据范围及提示】
样例解释:
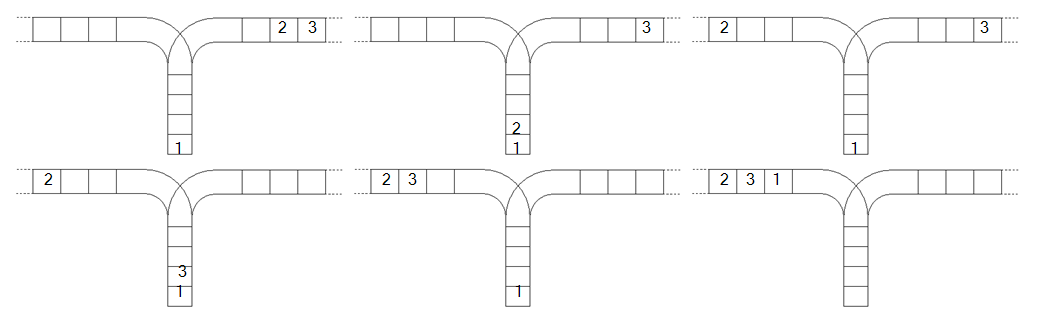
源代码: #include<cstdio> int n; long long ans=1; int main() //Catalan数。 { scanf("%d",&n); for (int a=1;a<=n;a++) ans=ans*(a*4-2)/(a+1); printf("%lld",ans); return 0; } /* 有必要详细地了解一下卡特兰数。 先用一道题来引出卡特兰数: 有10个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问有多少种排列方式。 解析: 我们可以先把这10个人从低到高排列,选择5个人排在第一排,那么剩下的5个人肯定是在第二排。 用0表示对应编号的人排在第一排,用1表示对应编号的人排在第二排,则含有5个0,5个1的序列,就对应一种方案。 比如:0000011111 就对应着: 第一排:0 1 2 3 4 第二排:5 6 7 8 9 比如:0101010101 就对应着: 第一排:0 2 4 6 8 第二排:1 3 5 7 9 所以问题相应的转换为满足条件的01序列有多少个。 观察规律,我们发现每个1的出现,前面必须有个相应的0,所以在从左到右的所有子序列中,0的个数总会大于等于1的个数。 那么这种数列究竟有多少种排列方式呢? 我们从左往右扫描,假设第一次出现1的个数等于0的个数是在第k位,那么在此之前,0的个数是大于1的个数的。在此之后,0的个数也是大于1的个数的,所以同理于进出栈问题。 即:f(n)=f(0)*f(n-1)+f(1)*f(n-2)+···+f(n-1)*f(0) Catalan公式:(令f(0)=0,f(1)=1) (1)f(n)=f(0)*f(n-1)+f(1)*f(n-2)+···+f(n-1)*f(0); (2)f(n)=C(2n,n)/(n+1); (3)f(n)=C(2n,n)-C(2n,n-1); 拓展问题: (1)一个栈的进栈序列为1 2 3 ··· n,询问有多少个不同的出栈序列; (2)在一个凸多边形中,通过作出若干条互不相交的对角线,把这个多边形划分成若干个三角形,询问不同划分的方案数; (3)给定N个节点,询问能构成多少种不同的二叉搜索树。 */
