距离咨询

【题目描述】

农夫约翰有N(2 <= N <= 40000)个农场，标号为1~N，有M(2 <= M <= 40000)条的不同的垂直或水平的道路连接着农场，道路的长度不超过1000。这些农场的分布就像下面的地图一样，在图中农场用F1~F7表示：

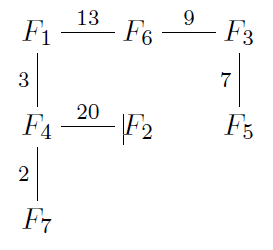
每个农场最多能在东西南北四个方向连接4个不同的农场，农场只会处在道路的两端，道路不会交叉而且每对农场之间有且仅有一条道路。约翰只知道每一条道路的信息如下：

从农场23往南经距离10到达农场17；

从农场1往东经距离7到达农场17；

······

现有一张如上的地图以及K个问题，每个问题包括两个农场的编号，询问它们之间的距离。

【输入描述】

第一行输入两个整数N和M；

接下来M行，每行输入四个整数F1、F2、L、D，分别表示两个农场的编号、道路的长度、F1到F2的方向N、E、S、W；

接下来一行输入一个整数K(1 <= K <= 10000)；

接下来K行，每行输入两个整数，表示2个农场。

【输出描述】

对于每个问题，输出一个整数，表示答案。

【样例输入】

7 6

1 6 13 E

6 3 9 E

3 5 7 S

4 1 3 N

2 4 20 W

4 7 2 S

3

1 6

1 4

2 6

【样例输出】

13

3

36

源代码：

#include<cstdio>
#include<algorithm>
using namespace std;
struct Node
{
    int S,To,Next;
}Edge[80001];
int m,n,Num(0),i[40001],Deep[40001],Head[40001],f[40001][22];
void Add(int t1,int t2,int t)
{
    Edge[++Num].To=t2;
    Edge[Num].S=t;
    Edge[Num].Next=Head[t1];
    Head[t1]=Num;
}
void DFS(int T,int S)
{
    Deep[T]=S;
    for (int a=Head[T];a;a=Edge[a].Next)
    {
        int t=Edge[a].To;
        if (!Deep[t]&&t!=1)
        {
            f[t][0]=T;
            i[t]=i[T]+Edge[a].S;
            DFS(t,S+1);
        }
    }
}
void Get_Father()
{
    for (int b=1;b<=21;b++)
      for (int a=1;a<=n;a++)
        f[a][b]=f[f[a][b-1]][b-1];
}
int Get_Same(int T,int S)
{
    for (int a=0;a<=21;a++)
      if ((1<<a)&S)
        T=f[T][a];
    return T;
}
int LCA(int t1,int t2)
{
    if (t1==1||t2==1)
      return 1;
    if (Deep[t1]<Deep[t2])
      swap(t1,t2);
    t1=Get_Same(t1,Deep[t1]-Deep[t2]);
    if (t1==t2)
      return t1;
    for (int a=21;a>=0;a--)
      if (f[t1][a]!=f[t2][a])
      {
        t1=f[t1][a];
        t2=f[t2][a];
      }
    return f[t1][0];
}
int main() //裸倍增LCA。
{
    scanf("%d%d",&n,&m);
    for (int a=0;a<m;a++)
    {
        char T;
        int t,t1,t2;
        scanf("%d%d%d %c",&t1,&t2,&t,&T);
        Add(t1,t2,t);
        Add(t2,t1,t);
    }
    i[1]=0;
    DFS(1,0);
    Get_Father();
    scanf("%d",&m);
    for (int a=0;a<m;a++)
    {
        int t1,t2;
        scanf("%d%d",&t1,&t2);
        int Ans=LCA(t1,t2);
        printf("%d\n",i[t1]+i[t2]-(i[Ans]<<1));
    }
    return 0;
}