绿豆蛙的归宿
【题目描述】
给定一个有向无环图,起点为1,终点为N,每条边都有一个长度,并且从起点出发能够到达所有的点,所有的点也都能够到达终点。绿豆蛙从起点出发,走向终点。
到达一个顶点时,如果有K条离开该点的道路,绿豆蛙可以选择任意一条道路离开该点,并且走每条路的概率为1/K 。
现在绿豆蛙想知道,从起点走到终点的所经过的路径总长度的期望值是多少。
【输入描述】
第一行输入2个整数N、M,代表图中有N个点、M条边;
第二行到第1+M行,每行输入3个整数a、b、c,代表从a到b有一条长度为c的有向边。
【输出描述】
输出一个数,表示从起点到终点路径总长度的期望值,四舍五入保留两位小数。
【样例输入】
4 4
1 2 1
1 3 2
2 3 3
3 4 4
【样例输出】
7.00
【数据范围及提示】
样例如图所示:
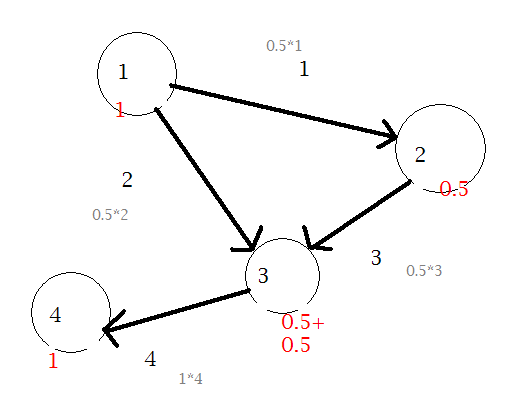
对于20%的数据,N <= 100;
对于40%的数据,N <= 1000;
对于60%的数据,N <= 10000;
对于100%的数据,N <= 100000,M <= 2*N。
源代码: #include<cstdio> #include<queue> using namespace std; struct Node { int To,S,Next; }i[200001]; queue <int> Q; int m,n,Num(0),Head[100001],Sum[100001],D[100001]; double f[100001]; void Add(int t1,int t2,int Length) //边表。 { i[++Num].To=t2; i[Num].S=Length; i[Num].Next=Head[t1]; Head[t1]=Num; } int main() { scanf("%d%d",&n,&m); for (int a=0;a<m;a++) { int t,t1,t2; scanf("%d%d%d",&t1,&t2,&t); Add(t2,t1,t); Sum[t1]++; } for (int a=1;a<=n;a++) D[a]=Sum[a]?Sum[a]:1; Q.push(n); while (!Q.empty()) //改造后的拓扑排序。 { int T=Q.front(); Q.pop(); f[T]/=D[T]; for (int a=Head[T];a;a=i[a].Next) { int t=i[a].To; f[t]+=f[T]+i[a].S; if (!(--Sum[t])) Q.push(t); } } printf("%.2lf",f[1]); //坑爹的double。 return 0; } /* 解题思路: 首先要引入数学期望的概念: 数学期望就是此结果乘以此结果的概率所求得的值。 由题意易得,从开头到结尾和从结尾到开头是相同的。 */

 浙公网安备 33010602011771号
浙公网安备 33010602011771号