表达式求值
栈的应用—表达式求值
表达式通常由三部分组成:①操作数②运算符③界限符(括号等)
常见表达式有以下几种:
-
中缀表达式:\(a+b\)、\(a\backslash b\)、\(a+b-c\)、\(a+b-c*d\)
特点:运算符在两个数中间
-
后缀表达式(逆波兰表达式):\(ab+\)、\(ab\backslash\)、\(ab+c-\)、\(ab+cd*-\)
特点:运算符在两个操作数后面
-
前缀表达式(波兰表达式):\(+ab\)、\(\backslash ab\)、\(-+abc\)、\(-+ab*cd\)
特点:运算符在操作数前面
1. 中缀表达式转后缀方法
遵循左优先原则。
①确定运算顺序
②选择下一个运算符,按照\([左操作数\) \(右操作数\) \(运算符]\)的方式组合成一个新的操作数
③如果还有运算符没被处理,继续②
如\(中缀表达式((15÷(7-(1+1)))\times3)-(2+(1+1))\)转换为后缀步骤:
- \(1\) \(1\) \(+\)
- \(7\) \(1\) \(1\) \(+\) \(-\)
- \(15\) \(7\) \(1\) \(1\) \(+\) \(-\) \(÷\)
- \(15\) \(7\) \(1\) \(1\) \(+\) \(-\) \(÷\) \(3\) \(\times\)
- \(15\) \(7\) \(1\) \(1\) \(+\) \(-\) \(÷\) \(3\) \(\times\) \(1\) \(1\) \(+\)
- \(15\) \(7\) \(1\) \(1\) \(+\) \(-\) \(÷\) \(3\) \(\times\) \(2\) \(1\) \(1\) \(+\) \(+\)
- \(15\) \(7\) \(1\) \(1\) \(+\) \(-\) \(÷\) \(3\) \(\times\) \(2\) \(1\) \(1\) \(+\) \(+\) \(-\)
2 后缀表达式计算
通过上面我们将中缀表达式转为后缀表达式\(15\) \(7\) \(1\) \(1\) \(+\) \(-\) \(÷\) \(3\) \(\times\) \(2\) \(1\) \(1\) \(+\) \(+\) \(-\)
计算后缀表达式也不难:从左往右扫描,每遇到一个运算符,就让运算符前面最近的两个操作数执行对应运算
合体为一个操作数。注意:两个操作数的左右顺序。
步骤:
- 第一个运算符是\(+\),先算\(1+1\)
- 第二个运算符是\(-\),\(7-2\)
- 第三个运算符是\(÷\),\(15÷5\)
- 第四个运算符是\(\times\),\(3\times3=9\)
- 第五个运算符是\(+\),\(1+1\)
- 第六个运算符是\(+\),\(2+2=4\)
- 最后一个运算符是\(-\),\(9-4\)得最后结果
3 代码实现
代码实现需要遵循以下几点:
①遇到操作数直接入栈
②遇到界限符'\((\)',直接入栈,遇到'\()\)',依次弹出栈内的运算符,直到栈顶元素为'\((\)'。
③运算符运算弹出规则,应该是:操作符栈顶运算符大于或等于当前输入运算符则弹出栈顶操作符。数字栈依次弹出两个数字\(num1,num2\),运算是\(num2+-...num1\)
\(\Large 例:计算中缀表达式((15÷(7-(1+1)))\times3)-(2+(1+1))\)
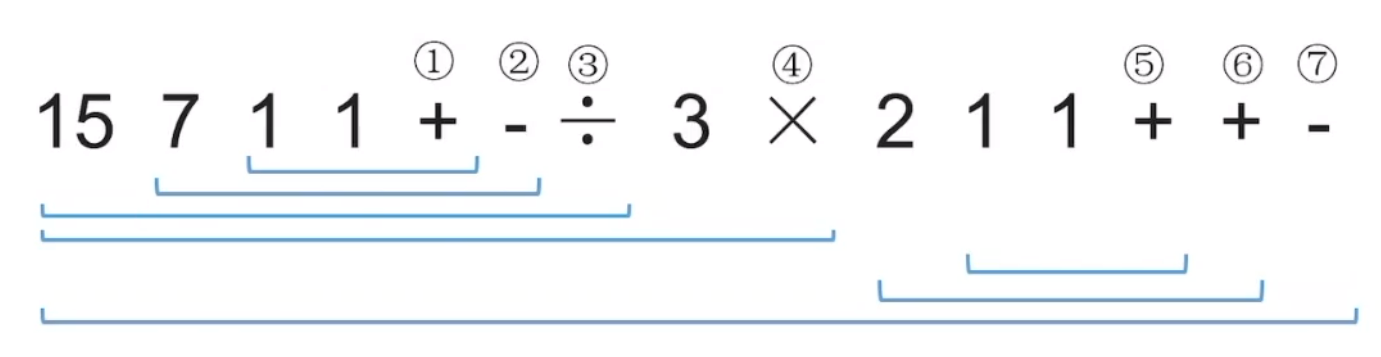
Ⅰ.先分析运算符生效顺序,如下图:

Ⅱ. 从左到右依次扫描入栈:操作符栈(charStack),操作数栈(numStack)
Ⅲ. 定义操作符优先级:\(+/-\)为\(A\),\(\times/÷\)为\(B\),\((\)为\(C\).
Ⅳ. 进行扫描运算:
①输入'\((\)',由于操作符栈为\(NULL\),直接入栈。
②输入'\((\)',操作符栈不为\(NULL\),且优先级等于操作栈顶的元素'(',但由于括号不参与运算,所以直接入栈。
③输入\(15\),数字直接入栈。
④输入'\(÷\)',由于'÷'优先级低于操作符栈顶元素'(',直接入栈。
⑤输入'\((\)',括号直接入栈。
⑥输入\(7\),数字直接入栈。
⑦输入'\(-\)','\(-\)'y优先级低于操作符栈顶元素'\((\)',入栈。
⑧输入'\((\)',直接入栈
⑨输入\(1\),入栈
⑩输入'\(+\)','\(+\)'优先级低于操作符栈顶元素'\((\)',入栈
⑪输入\(1\),入栈。此时栈中元素情况如下:
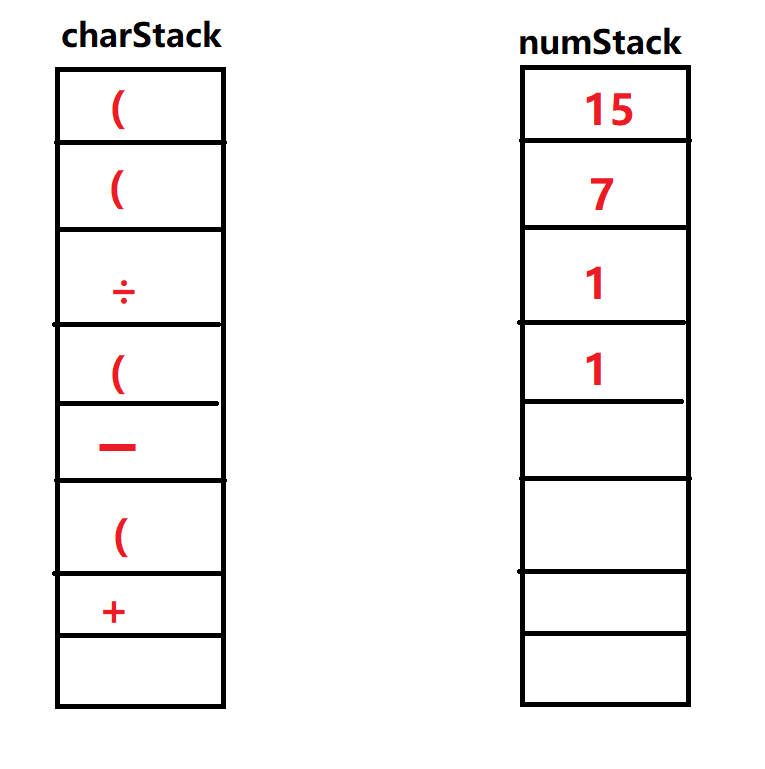
⑫输入'\()\)',栈顶操作符一次出栈直到为NULL或者为'\((\)'。此时弹出操作符栈顶元素'\(+\)',弹出操作数栈前两个元素\(1,1\)。之后运算\(1+1\)得到新的数字重新放回操作栈顶部,再次执行弹出元素为'\((\)',这次运算结束。
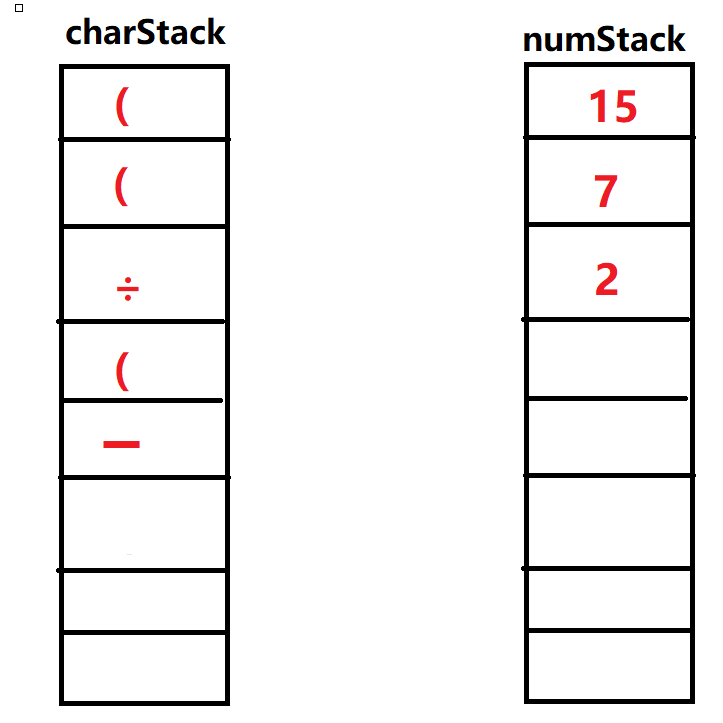
⑬输入')',再次重复上面,弹出操作符栈顶元素'\(-\)',弹出操作数栈两个元素\(2,7\),运算\(7-2\)。得到新的数字重新放回操作栈顶部,再次执行弹出元素为'\((\)',这次运算结束。
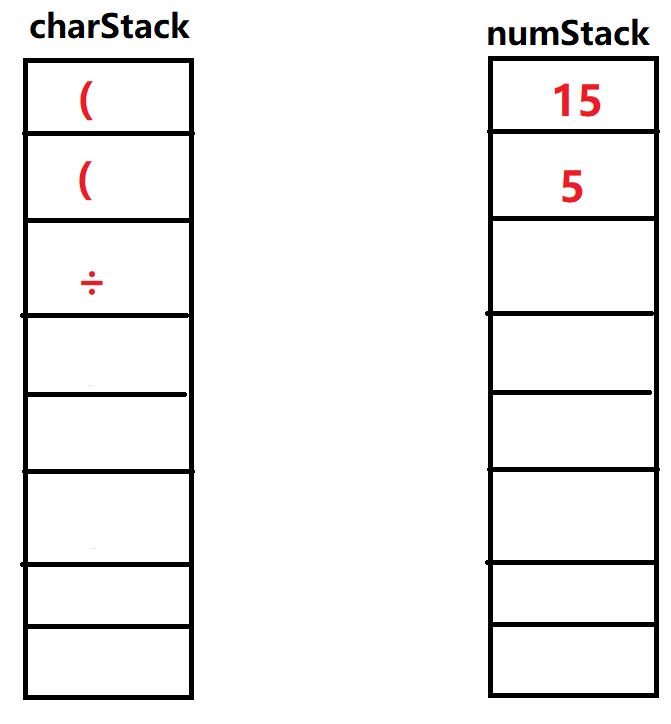
⑭输入'\()\)',重复上面过程,弹出操作符栈顶元素'\(÷\)',弹出操作数栈两个元素\(5,15\),运算\(15÷5\)。得到新的数字重新放回操作栈顶部,再次执行弹出元素为'\((\)',这次运算结束。
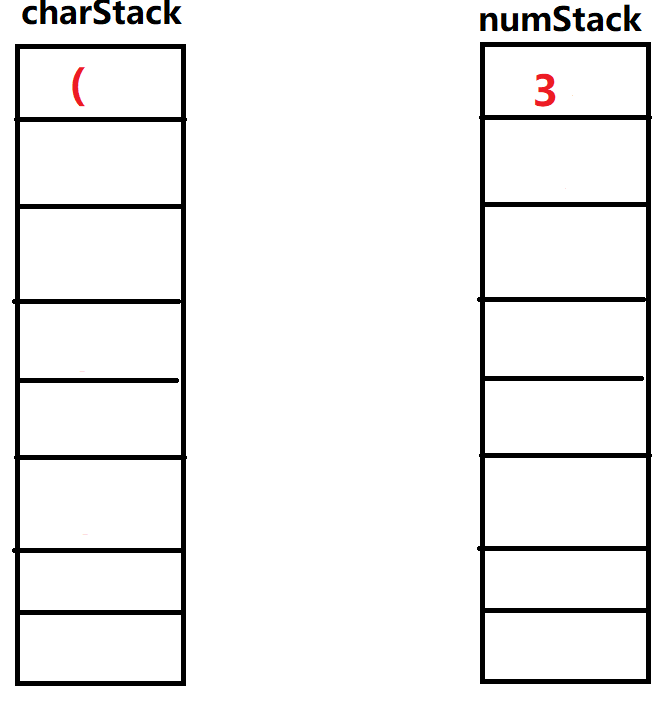
⑮输入'\(\times\)',此时操作符栈顶元素为'\((\)',优先级低于栈顶元素,直接入栈。
⑯输入'\(3\)',直接入栈
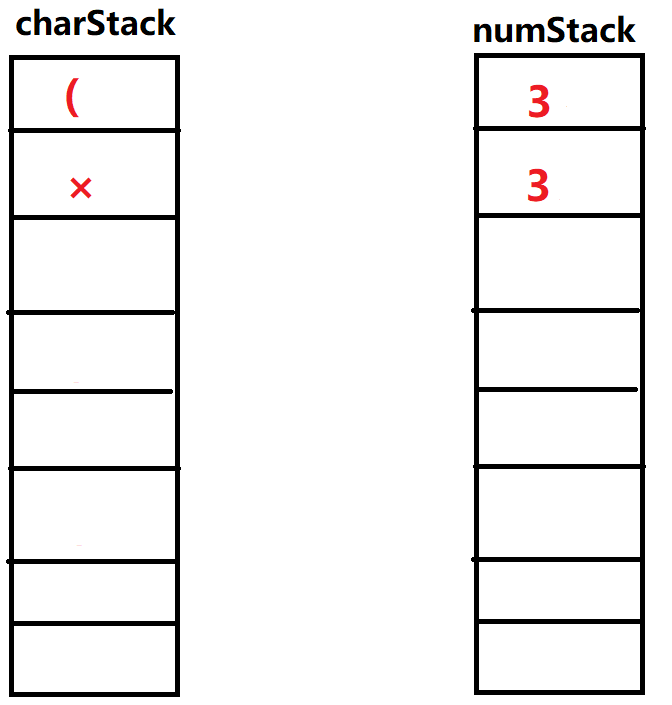
⑰输入'\()\)',弹出操作符栈顶元素'\(\times\)',弹出操作数栈两个元素\(3,3\),运算\(3\times3\)。得到新的数字重新放回操作栈顶部,再次执行弹出元素为'\((\)',这次运算结束。
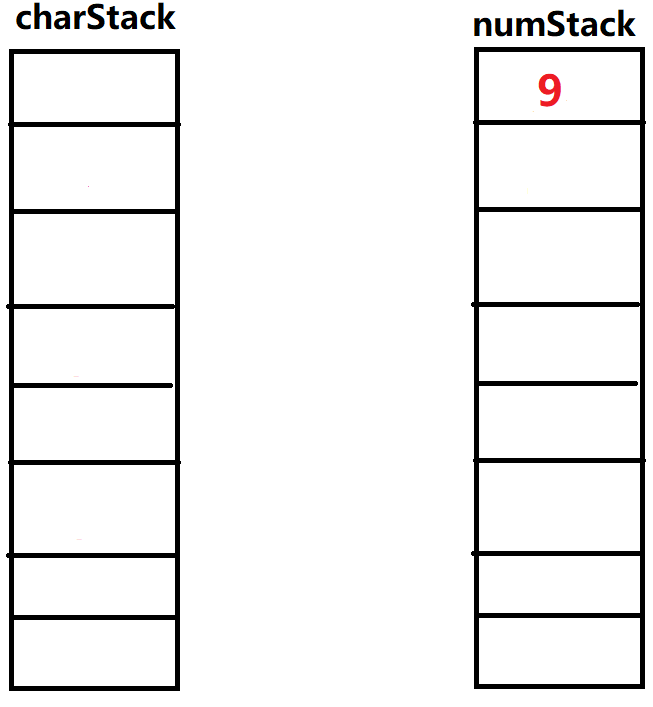
⑱输入'\(-\)',此时操作栈为NULL,直接入栈
⑲输入'\((\)',入栈
⑳输入\(2\),入栈
㉑输入'\(+\)',优先级小于操作栈顶元素'\((\)',入栈
㉒输入'\((\)',直接入栈
㉓输入\(1\),入栈
㉔输入'\(+\)',优先级低于操作栈栈顶元素'\((\)',入栈
㉕输入\(1\),入栈
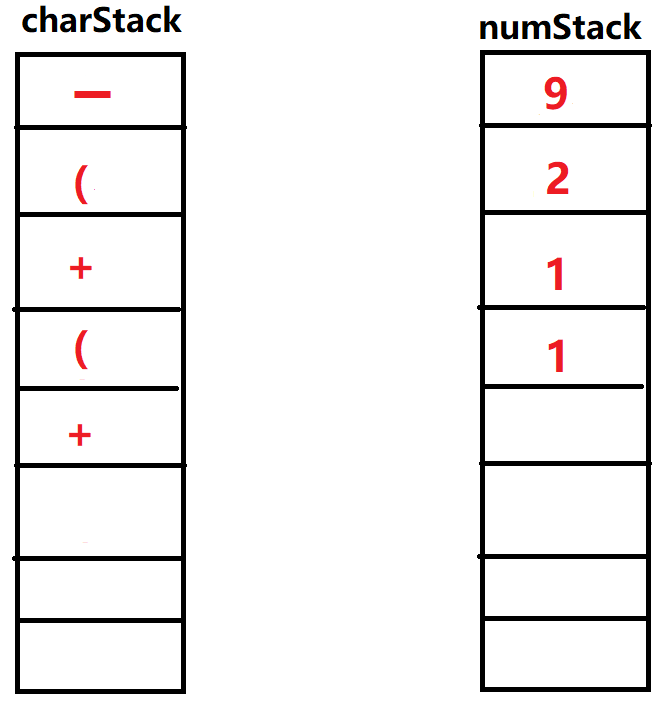
㉖输入'\()\)',弹出操作符栈顶元素'\(+\)',弹出操作数栈两个元素\(1,1\),运算\(1+1\)。得到新的数字重新放回操作栈顶部,再次执行弹出元素为'\((\)',这次运算结束。
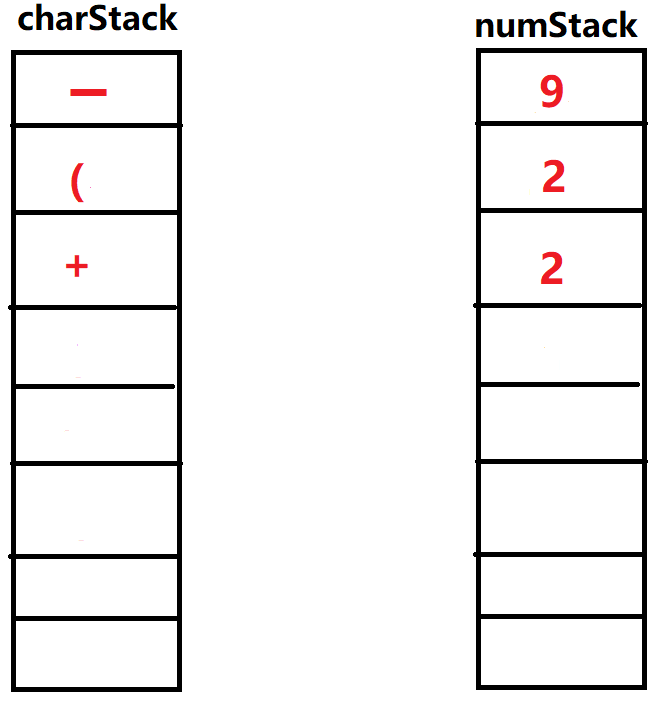
㉗输入'\()\)',弹出操作符栈顶元素'\(+\)',弹出操作数栈两个元素\(2,2\),运算\(2+2\)。得到新的数字重新放回操作栈顶部,再次执行弹出元素为'\((\)',这次运算结束。
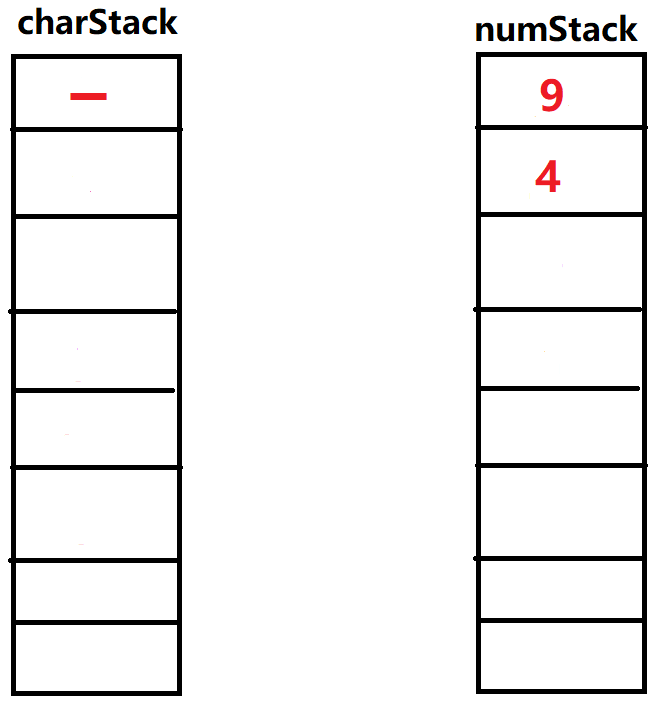
㉘弹出操作栈顶元素'\(-\)',弹出操作数栈两个元素进行最后运算,得到结果为\(5\)
详细代码
#include <bits/stdc++.h>
#include<string>
#define MaxSize 20
using namespace std;
char arrGrad(char s){
switch(s){
case '+':
return 'A';
case '-':
return 'A';
case '*':
return 'B';
case '/':
return 'B';
default :
return 'C';
}
}
//存放运算符
typedef struct linkC{
char data;
char grad;
struct linkC *next;
} *linkChar;
//存放运算数
typedef struct linkN{
int data;
struct linkN *next;
} *linkNum;
bool initCharNum(linkChar &c,linkNum &n,char (&s)[MaxSize]){
memset(s,'\0',sizeof(s));
c=(linkChar)malloc(sizeof(linkChar));
n=(linkNum)malloc(sizeof(linkNum));
if(c==NULL||n==NULL) return false;
c->next=NULL;
n->next=NULL;
return true;
}
//操作符入栈
bool pushChar(linkChar &c,char s){
linkChar p;
p=(linkChar)malloc(sizeof(linkChar));
if(p==NULL) return false;
if(s=='+'|s=='-'){
p->data=s;
p->grad=arrGrad(s);
p->next=c->next;
c->next=p;
return true;
}else if(s=='*'|s=='/'){
p->data=s;
p->grad=arrGrad(s);
p->next=c->next;
c->next=p;
return true;
}else if(s=='('){
p->data=s;
p->grad=arrGrad(s);
p->next=c->next;
c->next=p;
return true;
}else{
return false;
}
}
//操作数入栈
bool pushNum(linkNum &n,int e){
linkNum p;
p=(linkNum)malloc(sizeof(linkNum));
if(p==NULL) return false;
p->data=e;
p->next=n->next;
n->next=p;
return true;
}
//操作符出栈
char popChar(linkChar &c){
char s;
linkChar p;
if(c->next==NULL) return 'E';
s=c->next->data;
p=c->next;
c->next=p->next;
free(p);
return s;
}
//操作数出栈
int popNum(linkNum &n){
int i;
linkNum p;
if(n->next==NULL) return 0;
i=n->next->data;
p=n->next;
n->next=p->next;
free(p);
return i;
}
//获取操作符栈顶元素
char selectChar(linkChar &c,int e){
if(e) return c->next->data;
return c->next->grad;
}
//运算
void ope(linkChar &c,linkNum &n){
char popchar=popChar(c);
int num1=popNum(n);
int num2=popNum(n);
cout<<num2<<popchar<<num1<<endl;
switch(popchar){
case '+':
pushNum(n,num2+num1);
break;
case '-':
pushNum(n,num2-num1);
break;
case '*':
pushNum(n,num2*num1);
break;
case '/':
pushNum(n,num2/num1);
break;
}
}
void printStack(linkChar &c,linkNum &n){
while(c->next!=NULL){
cout<<"data:"<<c->next->data<<"grad::"<<c->next->grad<<endl;
c=c->next;
}
while(n->next!=NULL){
cout<<"result:"<<n->next->data<<endl;
n=n->next;
}
}
//字符转数字
int opeNum(char (&s)[MaxSize]){
int couts,sum=0;
for(int i=0;i<strlen(s);i++){
couts=s[i]-'0';
for(int j=i;j<strlen(s)-1;j++){
couts=couts*10;
}
sum+=couts;
}
memset(s,'\0',sizeof(s));
return sum;
}
int con=0;
//区分操作数和操作符
bool isCharNum(linkChar &c,linkNum &n,char s,char (&chrs)[MaxSize]){
int i;
if(s>='0'&&s<='9'){ //数字直接存入操作数栈
chrs[con++]=s;
return true;
}else if(s=='+'||s=='-'||s=='*'||s=='/'||s=='('||s=='!'){ //判断是否是操作符
if(strlen(chrs)>0) {
i=opeNum(chrs);
pushNum(n,i);
con=0;
}
if(c->next==NULL){ //操作符栈为空,直接入栈
pushChar(c,s);
return true;
}
if(selectChar(c,0)>=arrGrad(s)&&selectChar(c,1)!='('){ //不为空且栈顶操作符优先级大于等于当前所输入操作符元素,并且不是"("
while(c->next!=NULL&&c->next->grad>=arrGrad(s)&&c->next->data!='('){ //取出操作符进行运算操作
ope(c,n);
}
}
pushChar(c,s); //将当前输入操作符压入栈顶
return true;
}else if(s==')'){
if(strlen(chrs)>0||s=='!') {
i=opeNum(chrs);
pushNum(n,i);
con=0;
} //如果当前输入是")",弹出所有操作符进行运算,直到碰到"("
while(selectChar(c,1)!='('){
ope(c,n);
}
popChar(c); //弹出栈顶的"("
return true;
}else{
return false;
}
}
int main(){
char chr,chrs[MaxSize];
linkChar c;
linkNum n;
initCharNum(c,n,chrs);
while(chr!='!'){
cin>>chr;
isCharNum(c,n,chr,chrs);
}
ope(c,n);
printStack(c,n);
}
更多知识内容点这里


 浙公网安备 33010602011771号
浙公网安备 33010602011771号