LFSR产生伪随机码Verilog描述

LFSR介绍

LFSR即线性反馈移位寄存器，用于产生可重复的伪随机序列PRBS，该电路由n级触发器和一些异或门构成。每个时钟周期内，新的输入值反馈到LFSR内部各个触发器的输入端，输入值的一部分来源于LFSR的输出端，另一部分由LFSR各输出端进行异或运算得到。

LFSR的初始值被称为伪随机序列的种子。由n个触发器构成的LFSR电路可以产生周期为2^n-1的序列。

LFSR（线性反馈移位寄存器）计数器

LFSR计数器与常规计数器不同，不进行常规加减计数。通过重复出现的某个随机序列作为实现计数器的基础。其特点如下所示：

• 计数序列随机（实际上是伪随机），比如一个3位LFSR计数器的计数序列出现的规律是001，110，011，111，101，100，010，而不是依据二进制的计数方式来增加或减少。
• LFSR可以使用XOR反馈或者XNOR反馈，前者使用情况下全零为非法的状态，后者使用情况下全一为非法状态。
• 存在两种类型的LFSR（多到一，一到多）。对于多到一类型，多个触发器输出进行异或运算，输出结果进入一个寄存器，对于一到多类型，一个触发器的输出进入异或函数，计算结果驱动多个触发器

目前常用两种LFSR电路，分别是斐波那契LFSR和伽罗瓦LFSR。这两种电路都产生2^n-1个序列，但是一到多型LFSR具有更高的速度，因为其两个触发器间仅使用一个异或门。

斐波那契LFSR

斐波那契LFSR为多到一型LFSR，即多个触发器的输出经过异或逻辑来驱动一个触发器的输入。

反馈多项式为x^3+x^2+1

即x1的输入为x3和x2的输出异或后的结果，电路图如下所示：

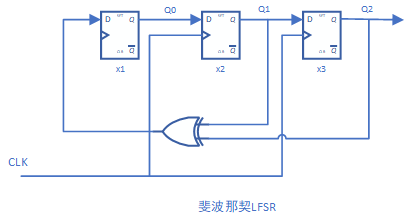
输出序列的顺序为：111-110-100-001-010-101-011-111

接下来进行电路的设计，RTL代码如下：

module lfsr(
    input        wire        clk,
    input         wire        rst,
    output        reg    [2:0]    q
    );

always @(posedge clk) begin
    if (rst) begin
        // reset
        q <= 3'b111;
    end
    else begin
        q <= {q[1],q[0],q[1]^q[2]};
    end
end

endmodule

testbench代码如下：

`timescale 1ns/1ps
module tb_lfsr();

reg                    clk;
reg                    rst;
wire    [2:0]        q;

initial begin
    clk=0;
    rst=1;
    #100
    rst=0;
end

always #10 clk = ~clk;

lfsr inst_lfsr (.clk(clk), .rst(rst), .q(q));


endmodule

modelsim仿真波形如下所示：

 

 

伽罗瓦LFSR

伽罗瓦LFSR为一到多型LFSR，即一个触发器的输出经过异或逻辑来驱动多个触发器的输入。

对于同样的反馈多项式x^3+x^2+1而言：

•  触发器x1的输入通常来源于触发器x2的输出
• x3（最高项）的输入通常来自于x1的输出
• 此多项式中剩余触发器的输入是x1的输出与前级输出异或的结果
• x2的输入由x1的输出与x3的输出通过异或运算得到

其电路图如下所示：

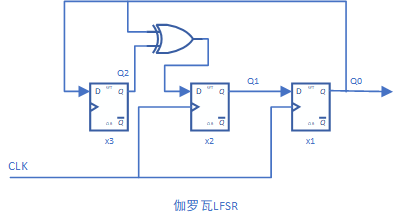
输出序列的顺序为：111-101-100-010-001-110-011-111

电路设计，RTL代码如下：

module lfsr2(
    input        wire        clk,
    input         wire        rst,
    output        reg    [2:0]    q
    );

always @(posedge clk) begin
    if (rst) begin
        // reset
        q <= 3'b111;
    end
    else begin
        q <= {q[0],q[2]^q[0],q[1]};
    end
end

endmodule

 testbench代码如下：

`timescale 1ns/1ps
module tb_lfsr();

reg             clk;
reg                rst;
wire    [2:0]    q;

initial begin
    clk = 0;
    rst = 1;
    #100
    rst = 0;
end

always #10 clk = ~clk;

lfsr2 inst_lfsr2 (.clk(clk), .rst(rst), .q(q));


endmodule

 modelsim仿真波形如下：

 

总结

 LFSR可以用于构建高速计数器，与常见的计数器相比，LFSR计数器具有速度快，消耗逻辑门少的特点。在扰码器/解码器的应用场景中，接收电路与发送电路采用同样的多项式即可进行通信。

在其他领域如密码系统、BIST（内建自测试）、快速以太网及吉比特以太网中都具有应用价值。

具体的用于产生最大长度伪随机序列的反馈多项式可以查阅文献：Table of Linear Feedback Shift Registers

 

Reference：

[1] Verilog高级数字系统设计计数与实例分析

[2] Ward R ,  Molteno T . Table of Linear Feedback Shift Registers.  2007.