【编译原理小记】：正规式到NFA，NFA化简为DFA
做编译原理作业是遇到的一类比较繁琐的题，记录一下。😘
大体流程
- 由正规式得出NFA的状态转换图
- 根据NFA的状态转换图写出NFA确定化为DFA的状态转换矩阵
- 根据上述矩阵中的重命名写出DFA重新命名状态转换矩阵表
- 化简所得到的DFA
- 画出DFA的状态转换图
正规式->NFA的状态转换图
要领比较简单，有点像连电路图，注意一下初态和终态的画法，以下是其他注意事项。
- ‘·’：一般会省去，由于连接前后各个字符串，画的时候当成串联下一状态就行
- ‘|’：或，连接时分出分支指向各自下一状态，像是并联
- ‘()’：优先计算，可以先单独处理成一个小单元，画好后再连头尾
- 上标‘*’：闭包，连向状态自己
- 上标‘+’：正闭包，我目前还没见过，个人感觉是比起上标‘*’前多加一个串联的状态
NFA的状态转换图->NFA确定化为DFA的状态转换矩阵
有点繁琐，是一个一遍遍扫描的过程。😟
- 第一行写上各列名称，分别为：重新命名、输入状态、n个输入字符
- 将初态名填入下一行的输入状态
- 观察图上在初态位置上，输入某个输入字符x后下一步可以转向哪些状态，并将它们依次写在表格（初态，x）中，若无状态可转移则不填，注意，转移向自己也要填上，状态间用“,”隔开
- 重复3的操作直到该行所有输入字符都已尝试
- 观察本行填写的结果，将每个单元格的结果都视作一个状态集合，若为空则无视，将所有新出现过的状态集合（注：不同顺序但同元素视为同一个状态集合）依次填入输入状态中的各格
- 仿照3、4的操作，记录各输入状态后续出现的状态集合，
- 当没有新的输入状态出现，也就是无新增可填时则结束
- 此时重新命名那一列还未填写，可根据自己的喜好为其填入字符名称，如A、B、C或1、2、3等，为了后续方便，建议尽可能简洁有序
至此矩阵的构建结束
写出DFA重新命名状态转换矩阵表
这一步很简单哦。😊
简要地来说，就是将上一步得到的矩阵去掉重命名那一列，将各输入状态的重命名回代到矩阵中去，全部其换掉，这一步就完成了！
化简所得到的DFA
这一步简要地将就是将各状态重新划分为块，但是有点绕。😔
- 首先将上一步得到的各输入状态划分为两个集合，一个叫非终态组，一个叫终态组。顾名思义，后者中的所有输入状态均包含终态；前者的则均不包含终态。
- 对于每个集合，我们进行这样的讨论：
2.1. 选择输入字符x进行输入，观察集合中各输入状态在输入x后转移的输入状态A1（即DFA矩阵中的（输入状态，x））、A2、A3...。
2.2. 若转移的输入状态均属于现在划分的同一集合，则无事发生；若不属于现在划分的同一集合，则计划在本轮操作后，将转移后不属于当前划分同一集合的都分开为新的集合。- 对每个集合讨论完后，我们将讨论中要分开的集合拆开，得到新的一组集合划分。
- 对得到的新的一组集合划分，重复2、3的操作，直至无法再分，得不出新的集合划分。
- 操作4结束后的一组集合划分中，若存在包含多个元素的集合，则将其替换为仅包含其中一个元素的集合（即单元素集合），得到新的一组集合划分，该结果即为化简结果。
- 重写化简后的矩阵，对于上一过程得到的矩阵，替换元素覆写其替换集合的所有元素，出现重复的便删除，化简完成！
画出DFA的状态转换图
胜利在望啊，同志们！💪
根据化简后的矩阵画出状态转移图，过于简单，不再赘述。
题目举例
以下是我自己作业的一次内容，供参考，如有错误请一定不吝指正！
题目描述
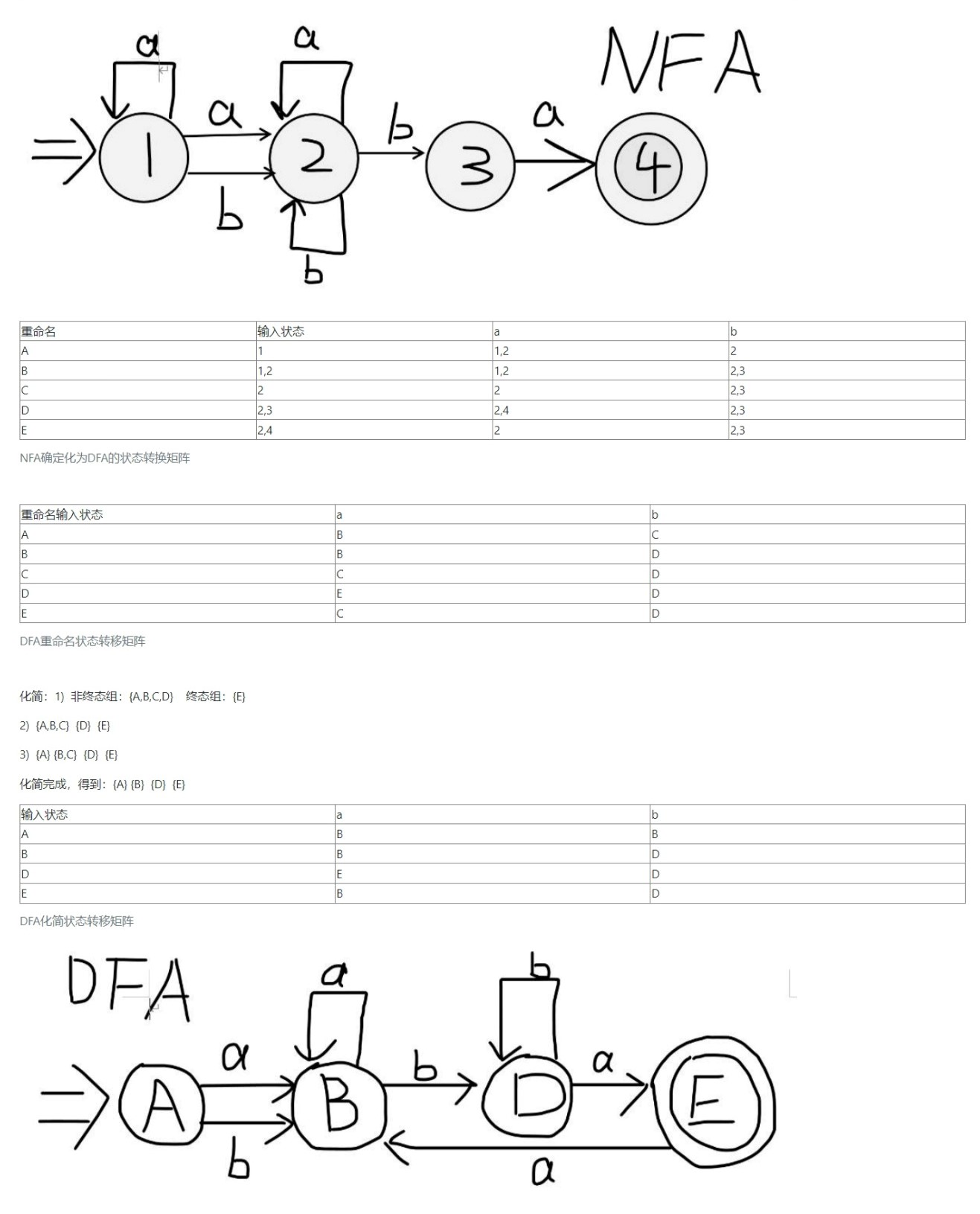
构造与正规式a（b|a)(a|b)ba等价的NFA，然后对NFA确定化为DFA，最后对DFA化简。要求NFA和DFA以图形方式描述。
解题示例
刚把得！😘
