图论技巧(2019/1/28之一)
使用注意
-
图论优化很实用,不过没练熟别轻举妄动。
-
不仅图论可用,搜索和遍历时也有奇效
-
-
善用数论知识
-
时时更新,熟练用法,创新结合
完善可能是个艰难的过程,不过坚持最重要。
——csy 2019.1.28
一些积累
1.存边
链式前向星存边

1 void add(int u,int v,int val) 2 { 3 e[++tot].v=v; 4 e[tot].val=val; 5 e[tot].next=head[x]; 6 head[x]=tot; 7 }
邻接表(vector优化)存边

1 void add1(int u,int v,int val) 2 { 3 e.push_back((A){v,val}); 4 e.push_back((A){u,val}); 5 int size=e.size(); 6 num[u]=size-1; 7 num[v]=size-2; 8 }//网络流存图法乱入,感觉图论可用,就是没有网络流的特殊需求下,显得有点取用麻烦且费力 9 void add2(int u,int v,int val) 10 { 11 e[u].push_back((A){v,val}); 12 e[v].push_back((A){u,val}); 13 }
评价
-
链式前向星最常用,不过重边删边麻烦
-
邻接表省空间
-
邻接矩阵耗空间,不过删边重边好处理,拓扑排序常用
例题
网络流诸题(滑稽
2.反向建边
评价
-
现在为止遇见的题都比较明显(
可能是因为我水吧),一般会有这么一句“k到n个点的最短/长距离”,如逛公园“如果1号点到N号点的最短路长为d”里十分不起眼又格外重要的一句 -
据说还可以判断某边是否在最短路上
对于一个有向图,我们从1号点跑一遍正向的最短路 dis,从n号点跑一遍反向的最短路 dis2,如果 dis1[x]+w(x,y)+dis2[y]=dis[n],那么我们就可以得出,这条边是在1到n的最短路上的。
当然如果是无向图的话直接跑就可以了。//就是不懂这个,什么叫直接跑
-
查资料的时候看见一个神奇的东西,并查集还能跑图,还能用反向边优化,想到这个的真是人才
例题
3.虚点连边
虚点连边是一种很有效的优化建边复杂度的方式。
评价
-
觉得这玩意儿和网络流里超级汇点/源点是一个东西
-
线段树里见过
-
思想很活,有些时候体感比正解难
-
一定要读题,线索在旮旮角角里
例题
-
首先回忆一下虚点适用范围之一:求其他点到给出点(n>1)最短距离。感觉很眼熟?对的,上面反向边的时候见过,那是不是每个点反向建边跑个最短路就解决了?spfa跑一百遍都成bi—(消音)
-
那怎么办?建一个虚点。向各个需要比较的点连一条边权为零的点,你只用跑一遍最短路维护各店到虚点最短路就能顺便维护其他点到给出点的最短距离了
-
那这和本题有什么关系?看看题意:“只要某个没有被占城市到某个被占城市不超过s距离,就是危险。”
-
十级中文转换一下,维护出每个城市到危险城市(给出点)的最短路,再判断一下与s的大小关系,标记一下,就维护出危险城市和安全城市了,接下来重新建图,赋钱为点权跑最短路就
现世安稳了 -
当我知道正解是跑bfs维护标记时我是崩溃的
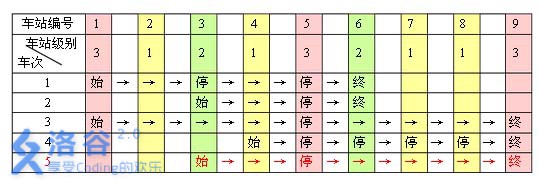
车站分级:
-
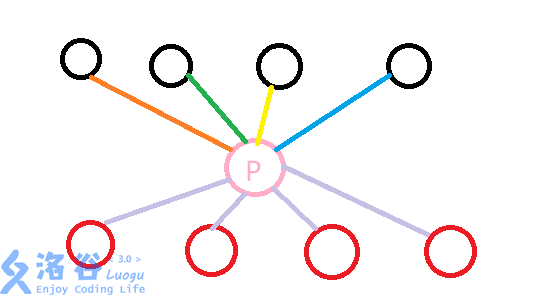
还是回忆虚点的作用:两个点集中的点要每一个都和对方集里每一个连一条边,减少其需要的边数,可以用o(n+m)的复杂度完成o(nm)的事情啦
-
似乎想到了以前的电话交换机
-
那么这和此题又有什么关系?都说了读题啦
![]()
-
把停站和始站分成两个集合,再建虚点,进行拓扑排序即可
-
感觉虚点只是起了优化建边时间的作用,总作用不大
-
据说可以用线段树合并做,推了一下时间复杂度大概o(nmlogn)吧
-
神奇的需要用并查集(
怎么哪里都有你)+虚点的一道题 -
重点是并查集的非递归写法,捡到宝了
4.线段树优化建边
评价
-
个人觉得这是上面虚点的升级版。
-
因为线段树的区间连续性和可查询调用任意区间性,当你要给例如2-6这个区间构图的时候,不如直接牵一条
红线在x点和2-6这个区间上,o(n)变o(1)有没有 -
注意线段树上的边权为零,边权赋在x->(i-j)上
例题
-
省选题啊,忐忑忐忑,题好长,肯定不简单
-
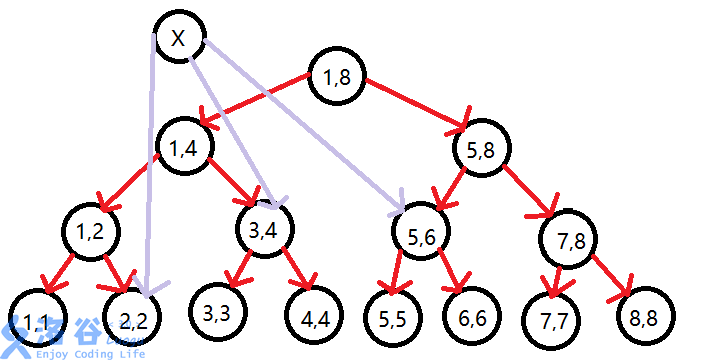
耶,裸题。进行单点与单点连有向边,进行单点与区间连有向边 ,进行区间与单点连有向边。然后求最短路就完了,只是区间怎么和点连边?
-
再建一棵树。
-
图就说明了一切,详细请观看江南柚子大佬的博客
5.拆点构图
评价
-
有些题很神,两个点之间有很多种情况,不能只跑个最短路,这个时候怎么办?
-
对,网络流的拆点带你飞
例题
飞行路线:
-
我自己也没搞懂……看题解吧。
5.图论除了图论还可以做什么?
-
背包,一个最短路搜过去,飞上天
-
据说可以做状压
-



 浙公网安备 33010602011771号
浙公网安备 33010602011771号