NOIp2018集训test-9-4
老张让我们2.5h考NOI%你题，喵喵喵？
因为今（我）天（实）的（在）题（太）鬼（弱）畜（了）了，我还只改了t1。
Problem A. reorder
考试的时候大家都写了最长不降子序列，然后全员10分，就很开心。
考虑中间一段不降的序列不变，然后剩余的一部分往前放一部分往后方，答案就是n-这段序列的长度
调一下第2组数据，发现直接求最长不降子序列是错的，因为可能在最长不降子序列中间有一部分没有被选的数，权值是在最长不降子序列的最小值和最大值之间的。
所以正确的答案只能是这样的
中间一段不降序列，其余点都在这一段最高点上面或者最低点下面(可以共线)
排序之后双指针扫就好了
注意直接扫会漏掉的部分，红色的部分要通过二分求出
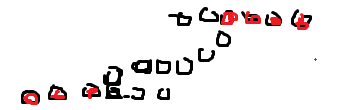
一开始我只二分了下面没有二分上面，但是题目数据是用脚造的，就过了，wys大佬告诉我之后，我随手造了一组数据就把之前的代码×了
9
1 1 4 2 3 4 4 5 5
改过后的代码
1 //Achen
2 #include<algorithm>
3 #include<iostream>
4 #include<cstring>
5 #include<cstdlib>
6 #include<vector>
7 #include<cstdio>
8 #include<queue>
9 #include<cmath>
10 #include<set>
11 #include<map>
12 #define Formylove return 0
13 #define For(i,a,b) for(int i=(a);i<=(b);i++)
14 #define Rep(i,a,b) for(int i=(a);i>=(b);i--)
15 const int N=1e6+7;
16 typedef long long LL;
17 typedef double db;
18 using namespace std;
19 int n;
20 vector<int>vc[N],vc2[N];
21
22 template<typename T>void read(T &x) {
23 char ch=getchar(); x=0; T f=1;
24 while(ch!='-'&&(ch<'0'||ch>'9')) ch=getchar();
25 if(ch=='-') f=-1,ch=getchar();
26 for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0'; x*=f;
27 }
28
29 struct node {
30 int a,pos;
31 friend bool operator <(const node&A,const node&B) {
32 return A.a>B.a||(A.a==B.a&&A.pos>B.pos);
33 }
34 }p[N];
35
36 #define ANS
37 int main() {
38 #ifdef ANS
39 freopen("reorder.in","r",stdin);
40 freopen("reorder.out","w",stdout);
41 #endif
42 read(n);
43 For(i,1,n) {
44 read(p[i].a); p[i].pos=i;
45 vc[p[i].a].push_back(i);
46 }
47 Rep(i,n,1) vc2[p[i].a].push_back(n-i+1);
48 sort(p+1,p+n+1);
49 int ans=n;
50 for(int l=1,r=1;l<=n;) {
51 while(r+1<=n&&p[r+1].pos<p[r].pos) r++;
52 int ll=l,rr=r;
53 if(ll-1>=1) {
54 int tt=lower_bound(vc2[p[l-1].a].begin(),vc2[p[l-1].a].end(),n-p[l].pos+1)-vc2[p[l-1].a].begin();
55 ll=ll-tt;
56 }
57 if(r+1<=n) {
58 int tt=lower_bound(vc[p[r+1].a].begin(),vc[p[r+1].a].end(),p[r].pos)-vc[p[r+1].a].begin();
59 rr=r+tt;
60 }
61 ans=min(ans,n-(rr-ll+1));
62 l=r+1; r=l;
63 }
64 printf("%d\n",ans);
65 Formylove;
66 }
67 /*
68 9
69 1 1 4 2 3 4 4 5 5
70 */
其实这个仍然漏掉了一种情况，就是在仅有两排的情况下，其实是可以这样选的，
需要枚举中间的分界线，我一开始以为这种情况可以某一块选完来等价替代，就把wys大佬和我自己糊弄到了，但是lyc巨佬发现，因为点的密度不同，所以是不能替换的。这部分代码我懒得写了。
-----------------------------------------9-20upd-----------------------------------------
Problem B. path
题解是spfa转移凸包，虽然我并不知道这个复杂度怎么证明。但是llj巨强无比，自适应辛普森水过了这道题。
平常自适应辛普森是eps递归减小的，但是这里这样的话会炸，所以一直用的同一个eps。
1 //Achen
2 #include<algorithm>
3 #include<iostream>
4 #include<cstring>
5 #include<cstdlib>
6 #include<vector>
7 #include<cstdio>
8 #include<queue>
9 #include<cmath>
10 #include<set>
11 #include<map>
12 #define Formylove return 0
13 #define For(i,a,b) for(int i=(a);i<=(b);i++)
14 #define Rep(i,a,b) for(int i=(a);i>=(b);i--)
15 const int N=807,M=807;
16 typedef long long LL;
17 typedef long double db;
18 using namespace std;
19 int n,m,s,t,x[M],y[M];
20
21 template<typename T>void read(T &x) {
22 char ch=getchar(); x=0; T f=1;
23 while(ch!='-'&&(ch<'0'||ch>'9')) ch=getchar();
24 if(ch=='-') f=-1,ch=getchar();
25 for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0'; x*=f;
26 }
27
28 int ecnt,fir[N],nxt[M],to[M];
29 db val[N];
30 void add(int u,int v) {
31 nxt[++ecnt]=fir[u]; fir[u]=ecnt; to[ecnt]=v;
32 nxt[++ecnt]=fir[v]; fir[v]=ecnt; to[ecnt]=u;
33 }
34
35 queue<int>que;
36 db dis[N];
37 int vis[N];
38 #define inf 1e18
39 #define EPS 1e-5
40 int dcmp(db x) { return fabs(x)<=EPS?0:(x>0?1:-1); }
41
42 db spfa() {
43 que.push(t);
44 For(i,1,n) dis[i]=inf;
45 dis[s]=0;
46 que.push(s);
47 while(!que.empty()) {
48 int x=que.front();
49 que.pop(); vis[x]=0;
50 for(int i=fir[x];i;i=nxt[i]) {
51 if(dcmp(dis[to[i]]-dis[x]-val[i])>0) {
52 dis[to[i]]=dis[x]+val[i];
53 if(!vis[to[i]]) {
54 vis[to[i]]=1;
55 que.push(to[i]);
56 }
57 }
58 }
59 }
60 return dis[t];
61 }
62
63
64 double f(double a) {
65 For(i,1,m) {
66 val[i*2]=a*x[i]+(1.0-a)*y[i];
67 val[i*2-1]=val[i*2];
68 }
69 return spfa();
70 }
71
72 double sim(double x,double y) {
73 double mid=((x+y)/2.0);
74 return (y-x)/6.0*(f(x)+4.0*f(mid)+f(y));
75 }
76
77 double calc(double l,double r) {
78 double mid=((l+r)/2.0);
79 double tp=sim(l,mid)+sim(mid,r),tpp=sim(l,r);
80 if(dcmp(tp-tpp)==0) return tp+(tp-tpp)/15.0;
81 else return calc(l,mid)+calc(mid,r);
82 }
83 /*
84 double calc(double l,double r) {
85 double mid=((l+r)/2.0);
86 db ls=f(l),rs=f(r),ms=f(mid);
87 if(fabs(ls+rs-ms*2.0)<=EPS) return ms*(r-l);
88 else return calc(l,mid)+calc(mid,r);
89 }
90 */
91
92 #define ANS
93 int main() {
94 #ifdef ANS
95 freopen("path.in","r",stdin);
96 freopen("path.out","w",stdout);
97 #endif
98 read(n); read(m); read(s); read(t);
99 For(i,1,m) {
100 int u,v;
101 read(u); read(v);
102 add(u,v);
103 read(x[i]); read(y[i]);
104 }
105 db ans=calc(0,1);
106 printf("%Lf\n",ans);
107 Formylove;
108 }
