洛谷 P2507 [SCOI2008]配对

传送门

（讲道理）一道很简单的题，可惜我实在zz到了一种境界。

首先都可以匹配的情况下，两个数组分别排个序对应匹配肯定是最优的，实在太蠢的我不知道如何证明，就画了个丑陋的图。

可以发现不交叉一定不会更劣。

 

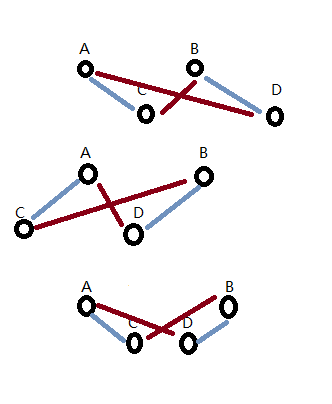
然后有一些是不能匹配的情况下，容易想到到肯定是跟它附近的几个交换。发现最多也不会跟它距离超过2的匹配，如图：

若是D和E匹配，一定不是最优。

考虑把三把叉中的一把拆掉，最坏情况下，A,B,C中的一个等于E，不能换，D等于另一个F,G,H中的一个，不能换，也就是两个交叉的可能都无法拆，但是是三个的话一定至少有一个可拆。

然后就直接dp搞了。

 

//Twenty
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<vector>
#include<cstdio>
#include<cmath>
#include<queue>
#include<ctime>
#define INF 0xfffffff 
typedef long long LL;
using namespace std;
const int maxn=1e5+5;
int n;
LL f[maxn],a[maxn],b[maxn];

template<typename T> void read(T &x) {
	char ch=getchar(); T f=1; x=0;
	while(ch!='-'&&(ch<'0'||ch>'9')) ch=getchar();
	if(ch=='-') f=-1,ch=getchar();
	for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
	x*=f;
}

LL c(int i,int j) {
	LL res=abs(a[i]-b[j]);
	return res==0?INF:res; 
}

void work() {
	sort(a+1,a+n+1);
	sort(b+1,b+n+1);
	for(int i=1;i<=n;i++) {
		f[i]=f[i-1]+c(i,i);
		if(i>1) f[i]=min(f[i],f[i-2]+c(i,i-1)+c(i-1,i));
		if(i>2) f[i]=min(f[i],f[i-3]+c(i,i-2)+c(i-1,i-1)+c(i-2,i));
		if(i>2) f[i]=min(f[i],f[i-3]+c(i,i-2)+c(i-1,i)+c(i-2,i-1));
		if(i>2) f[i]=min(f[i],f[i-3]+c(i,i-1)+c(i-1,i-2)+c(i-2,i));
	}
	printf("%lld\n",f[n]);
}

void init() {
	read(n);
	for(int i=1;i<=n;i++) { read(a[i]); read(b[i]); }
}

int main() {
#ifdef DEBUG
	freopen(".in","r",stdin);
	freopen(".out","w",stdout);
#endif
	init();
	work();
	return 0;
}