k-shape :Efficient and Accurate Clustering of Time Series
k-shape: Efficient and Accurate Clustering of Time Series
01 研究背景意义
时间序列：数据序列包含关于时间的显式信息(例如股票、音频、语音和视频)，或者如果可以推断值的顺序(例如流和手写)
几乎每个学科都出现了大量的时间序列，包括天文学、生物学、气象学、医学、工程等，时间序列的普遍存在使得人们对此类数据的查询、索引、分类和聚类产生了浓厚的兴趣。在所有应用于时间序列数据的技术中，聚类是使用最广泛的。通过聚类，我们可以 识别和总结底层数据中有趣的模式和相关性，时间序列聚类不仅作为一种独立研究方法，还作为其他任务的预处理步骤或子程序。
大多数时间序列分析技术主要依赖于距离度量的选择。一般认为距离度量的选择比聚类算法本身更重要。
时间序列聚类主要依赖于经典的聚类方法，要么用更适合时间序列的距离度量代替默认的距离度量，要么将时间序列转换为静态数据，以便现有的聚类算法可以直接使用。
然而，聚类算法的选择会影响:
(1)准确性，每种方法表达聚类的同质性和分离性不同;
(2)效率，不同方法的计算成本不同。
例如，与k-means或k-medoids等划分方法相比，光谱聚类或层次聚类更适合于识别基于密度的聚类。
另一方面，k-means方法比层次方法或k-medoids方法效率更高。
目前的基于形状的聚类方法，其距离度量是尺度和位移不变的，有两个主要缺点
(i) 依赖于复杂的的计算方法或距离度量，无法扩展到大量的数据;
(ii) 只针对特定领域，或者其有效性仅在有限的数据集上显示。
此外，基于形状的聚类方法通过序列坐标的局部非线性比对来处理相位不变性，但是全局比对通常就足够了。
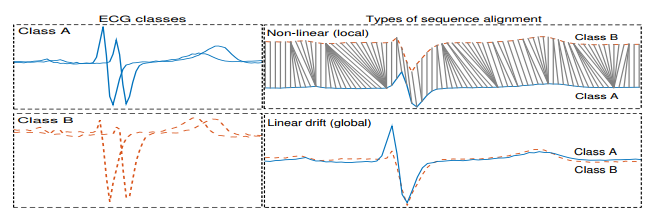
例如，对于图中的心电数据集，全局比对可以揭示两类序列模式的潜在差异，而非线性对齐可能匹配每个序列相应的变化，使得难以区分两类。
02 时间序列距离度量
归一化互相关NCC （Normalized cross-correlation）: 描述两个样本之间的相关性，取值为（-1，1）
NCC值越小，两样本越不相似；NCC值越大，两样本越相似。
相关系数：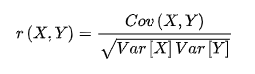
其中，Cov(X,Y)为X与Y的协方差，Var[X]为X的方差，Var[Y]为Y的方差
基于形状的时间序列距离（SBD）：
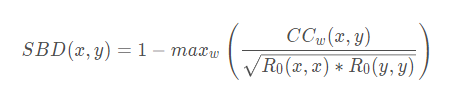
SBD值越小，序列的相似性越高，反之相似性越低。
03 时间序列形状提取
时间序列分析中的许多任务依赖于通过一个序列得到一组时间序列的方法。这个序列通常被称为平均序列，在聚类中，被称为质心。质心提取的关键在于距离度量的选择。
提取平均序列的最早方法是计算所有序列对应坐标的算术平均值。K-means算法就是采用这种方式。
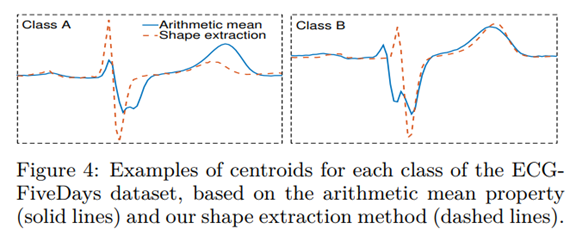
可以看出这种方式计算的质心没有很好地捕捉这类序列的特征，效果没有基于形状提取的质心好。
本文把质心计算视为一个优化问题，其目标是找到与类内所有其他时间序列之间距离平方和的最小值。
基于SBD距离度量的时间序列质心计算：
首先需要对类内所有的时间序列计算一个最佳的偏移量，把前一次计算得到的聚类中心作为参考并把所有的序列与这个参考的序列对齐，进行迭代聚类。
04 K-shape算法
距离度量计算：在分配步骤中，算法通过将每个时间序列与所有计算出地质心进行比较，并将每个时间序列分配给最接近质心地聚类来更新聚类中的成员关系.
聚类中心计算：在细化步骤中，更新聚类中心以反映前一步中聚类成员的变化。
05 实验结果
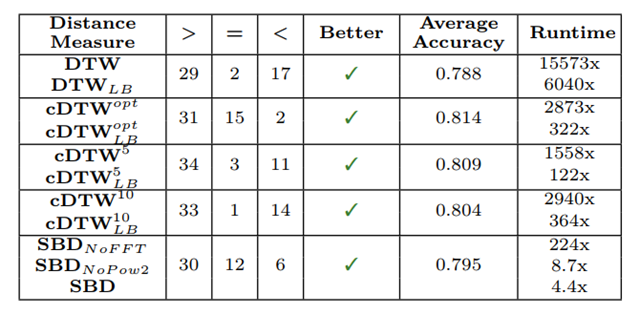
06 总结
1）互相关度量(如SBD)作为时间序列距离度量具有很好的效果，且速度要快得多
2）k-Shape是一种高精度、高效率的时间序列聚类方法。
3）聚类方法的选择与距离度量的选择同样重要，但聚类方法的选择被认为不如距离度量重要
4）对聚类算法距离度量和质心计算的不适当修改会降低其性能
