Zigzags CodeForces - 1400D

 

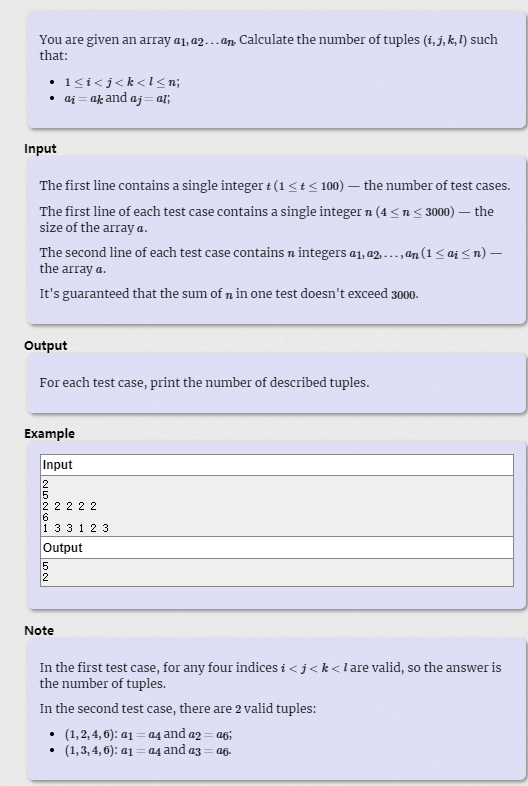
给出一组数：

寻找四元组的个数 

（i，j，k，l）其中a[i]=a[k]，并且a[j]=a[l]

刚看到这个题的时候想到了记录每个数的个数，然后求前缀和以及后缀和。先枚举i和k，当a[i]和a[k]相等时，在枚举i和k之间的数，然后在将前缀和与后缀和相乘，但是这样复杂度是o(n^3)，显然过不了。看了大佬的blog，发现有个更好的思路，我们现在枚举了i和k对吧，i-----k，而题目的要求是k---i---k---i，那就直接在i左边找个K并且在k后边找个i然后将他们出现的次数相乘就完了呗！

code:

 

#include<bits/stdc++.h>
using namespace std;
const int N=3e3+7;
long long  preious_sum[N][N];//表示sum[i][j]表示前i个数，j出现的次数
long long later_sum[N][N];
int arr[N];
int main(){
    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        for(int i=1;i<=n;i++) {
            cin>>arr[i]; 
            preious_sum[i][arr[i]]++;
            later_sum[i][arr[i]]++; 
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                preious_sum[i][j]+=preious_sum[i-1][j];
            } 
        }
        for(int i=n;i>=1;i--){
            for(int j=1;j<=n;j++){
                later_sum[i][j]+=later_sum[i+1][j];
            } 
        }
        long long  ans=0;
        for(int i=1;i<=n;i++){
            for(int j=i+1;j<n;j++){
                ans+=preious_sum[i-1][arr[j]]*later_sum[j+1][arr[i]];
            }
        }
        cout<<ans<<endl;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++)
                later_sum[i][j]=preious_sum[i][j]=0;
        }
    }


    return 0;
}

 另外一种写法。

code:

#include <stdio.h>
#define maxn 3010
#define LL long long
int a[maxn],cnt[maxn];
int main(){
    int t,n,i,j,sum;
    LL ans;
    scanf("%d",&t);
    while(t--){
        scanf("%d",&n);
        for(i=1;i<=n;i++)scanf("%d",&a[i]);
        for(i=1;i<=n;i++)cnt[i]=0;
        ans=0;
    //i1---j2
    //当前循环枚举的是i1和j2,cnt[]记录的是a[i1]出现的次数.
    //j1---i1---j2---i2
    //当枚举到i1=i,j2=j时，sum记录的是从i到j各个数出现的和，而cnt[k]就是在i1之前元素k出现的次数。sum累加就相当于寻找a[j1]=a[j2]的过程
    //当a[i]==a[j]的时候，说明i2找到了，i2=j，然后就可以更新答案了，更新完之后，j继续往后，因为后边可能还会有和a[i]相等的元素，找到再累加。
        for(i=1;i<=n;i++){
            sum=0; 
            for(j=i+1;j<=n;j++){
                if(a[i]==a[j])ans+=sum;
                sum+=cnt[a[j]];
            }
            cnt[a[i]]++;//第i个数出现的次数
        }
        printf("%lld\n",ans);
    }
    return 0;
}