E - Coprime

 

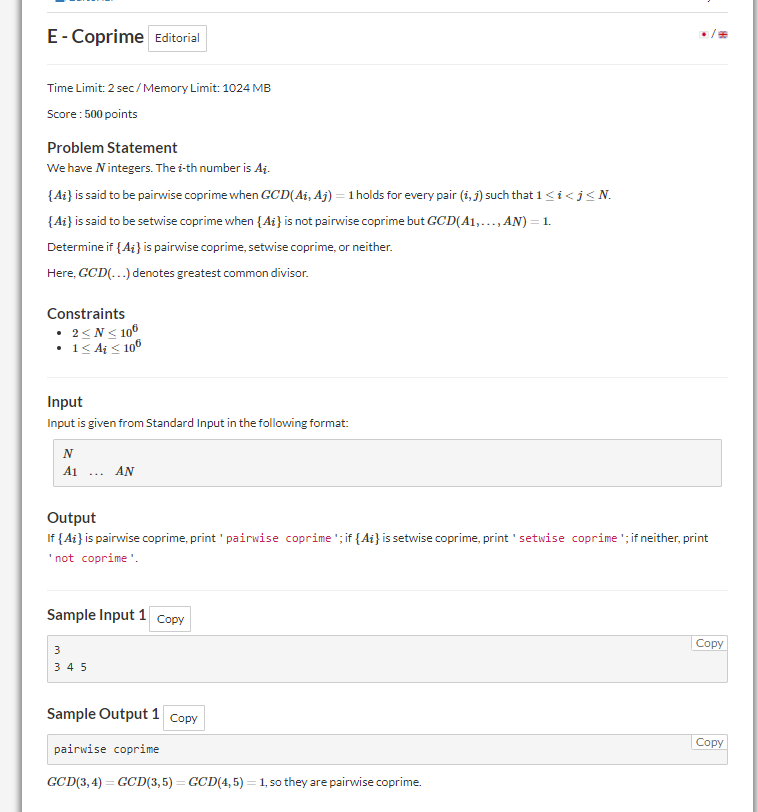
这是一个很有意思的题目，题目大意比较简单，当给出的n个数两两互质时，输出“pairwise coprime”，否则至少存在两个数不互质并且所有数的GCD=1，那么输出”setwise coprime“，如果说这俩条件都不满足的话，那就输出“not coprime”。

题解：这个问题可以转化为如何判断n个数两两互质，也就是说每两个数不存除1之外的公因数。我们注意到数据范围是1e6，暴力o(n^2)肯定是不行的。该怎么优化呢？

　　注意到“每两个数不存除1之外的公因数”，我们可以枚举公因数i，那么如果说一个数含有i这个因子，那么他一定是i的整数倍。然后我们用一个数组num保存每个数出现的次数，当枚举公因子i的时候，在加一个循环来枚举i的倍数 x=i*k 。（最大是x最大是1e6）。然后累加num[x]，如果大于1的话，那就说明至少存在两个数，他们的公因子为i。

code:

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+3;
int num[N];
int main(){
    int n,x;
    cin>>n;
    int z=0;
    for(int i=1;i<=n;i++){
        cin>>x;
        num[x]++;
        z=__gcd(z,x);
    }
    if(z!=1){
        cout<<"not coprime"<<endl;
        return 0;
    }
    
    for(int i=2;i<N;i++){
        int cnt=0;
        for(int j=i;j<N;j+=i){
            cnt+=num[j];
        }
        if(cnt>1) {
            cout<<"setwise coprime"<<endl;
            return 0;
        }
    }
    cout<<"pairwise coprime"<<endl;
    return 0;
}