归并排序是众多排序方法中比较稳定的一种排序。时间复杂度是o(nlogn)，是一种较优的排序方法。
归并排序是一种典型的分治法，其基本思想就是将大区间划分为小区间，先对小区间进行排序，然后在通过两个有序的小区间归并为一个有序的大区间。首先对待排序数组以二叉树的形式进行分割；
比如说对数组[5,4,3,2,1,0]，分割后就变成了这样的形式。叶子节点只含有一个点，一定是有序的。然后从叶子节点开始依次向上进行合并，处理顺序就是二叉树的后序遍历顺序一样。
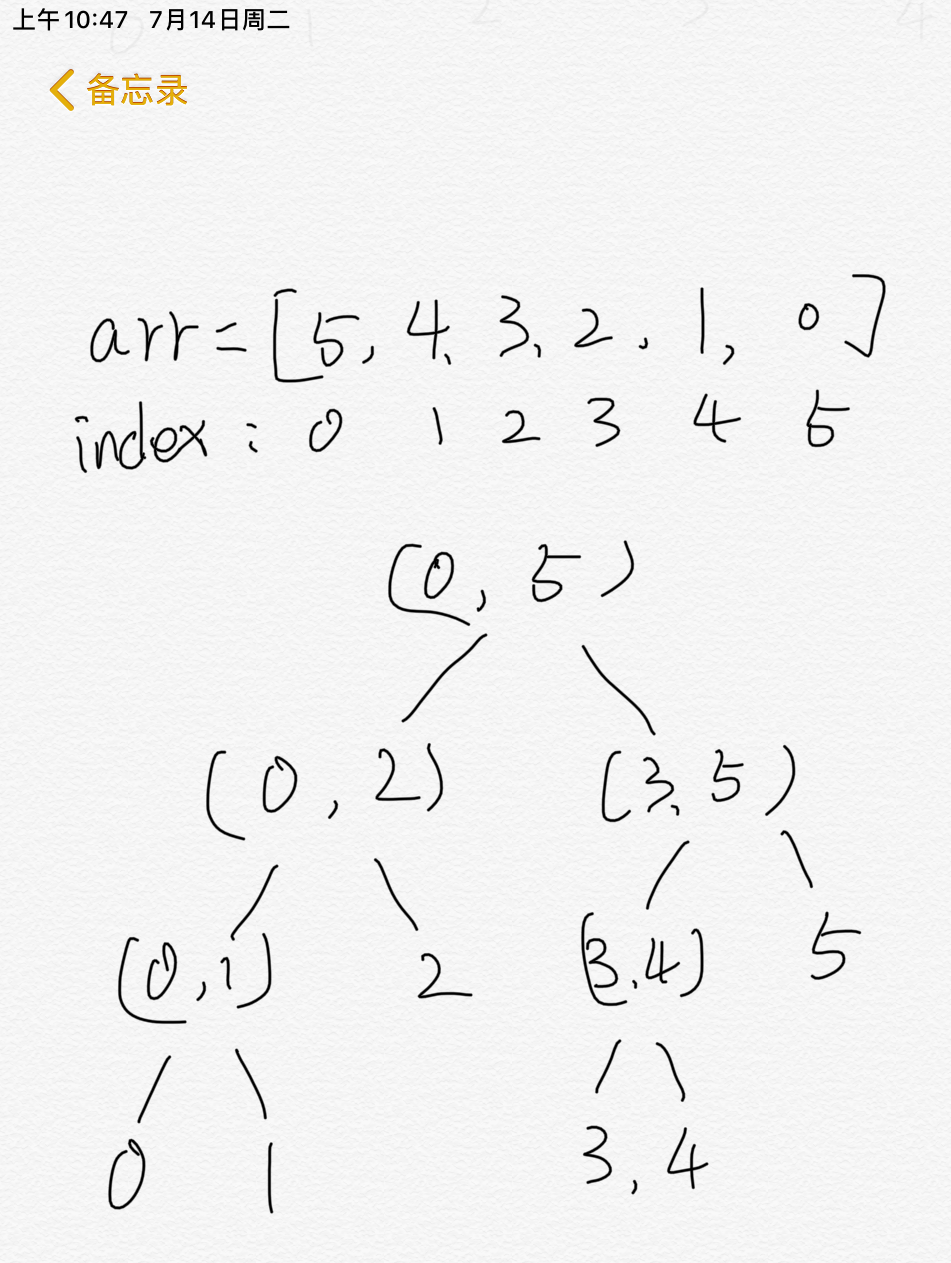
合并的过程就是每两个有序的区间合并成一个大区间。
看一下代码，代码还是比较好理解的。
code:
void merge(int a[],int l,int r,int mid){ for(int i=l;i<=r;i++) tmp[i]=a[i];// 暂时保存a当中的数 int i=l,j=mid+1; for(int k=l;k<=r;k++){ if(i>mid)a[k]=tmp[j++];//左边区间的数处理完毕，只剩下右边的数。 else if(j>r)a[k]=tmp[i++];//右边区间的数处理完毕，只剩下左边的数。 else if(tmp[i]>tmp[j]) {//比较左右区间的数字，取小的。 a[k]=tmp[j++]; } else a[k]=tmp[i++]; } } void merge_sort(int a[],int l,int r){ if(l>=r) return ; int mid=(l+r)/2; //分 merge_sort(a,l,mid); merge_sort(a,mid+1,r); //治 merge(a,l,r,mid); }
通过归并排序求数组的逆序数。
其思路就是在合并的过程中，
比如说此时的区间为
[a1,a2,a3,a4,b1,b2,b3,b4]
左半部分区间为[a1,a2,a3,a4]，一定是有序的，假设是从小到大的，右半部分的区间为[b1,b2,b3,b4]也一定是有序的。
假设左半部分比较到a2,下标为i，右区间比较到了b2，下标为j，如果说b2<a2，也那么b2一定排在a2的前边，又因为i<j，所以说一定会产生逆序对(a2,b2)，又因为a3>a2>b2，并且a3的下标也一定小于b2的下标，所以说(a3,b2)也是逆序对。因此我们可以找到b2的逆序对数为(mid-i+1)，mid为左边区间的右边界。
并且这个逆序数可以看做b2的左边比b2大的数的个数。若求b2左边比b2小的数的个数呢？当然这就不是逆序数了，这时我们只需要把从小到大改为从大到小排就可以了，想想看，从大到小排，两个子区间肯定也是从大到小的顺序，首先应该满足在b2的左边，如果b2大于左区间的一个数的吗，那么他肯定大于左区间该数右边的数。也就和求逆序数的方法一样了。
如果让求b2右边比它大的数呢？我们需要把原数组逆序一下，然后求从小到大求逆序数，求b2右边比它小的数，把原数组逆序然后从大到小求逆序数的个数。
