食物链 POJ - 1182 (并查集的两种写法)

这是一个非常经典的带权并查集，有两种写法。

1 边权并查集

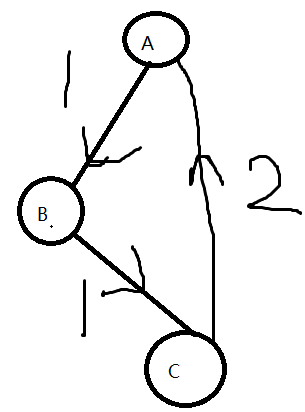
规定一下，当x和y这条边的权值为0时,表示x和y是同类，当为1时，表示x吃y，当为2时，表示x被y吃。

一共有三种状态，如图，当A吃B，B吃C时，C必须吃A，路径压缩后，A被C吃。

然后就是带权并查集的模板了。

判断条件，当x和y在同一颗树上是，

 

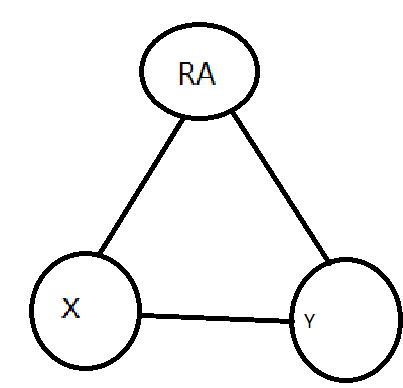
 如果说，x和y之间的关系是0，那么x和RA与Y和RA之间的关系必须相同才行。x和Y之间的关系是1，当S[y]=2时，S[x]=1,当s[y]=1时，s[x]应等于0，才能满足

所以判断条件为(s[x]-s[y]+3)%3=relation.

code：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e5+7;
int fa[N];
int sum[N];
int find(int x){
    if(fa[x]==x) return x;
    else {
        int c=find(fa[x]);
        sum[x]=(sum[x]+sum[fa[x]]+3)%3;
        return fa[x]=c;
    }
}
bool unite(int x,int y,int z){
    int fx=find(x);
    int fy=find(y);
    if(fx!=fy){
        fa[fx]=fy;
        sum[fx]=(sum[y]-sum[x]+z+3)%3;
        return 0;
    }
    else if((sum[x]-sum[y]+3)%3==z) return 0;
    else return 1;
}
int main(){ 
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;i++){
        fa[i]=i;
        sum[i]=0;
    }
    int ans=0;
    int d,x,y;
    for(int i=1;i<=m;i++){
        scanf("%d%d%d",&d,&x,&y);
        if(x>n||y>n||(d==2&&x==y)) {
            ans++;
            continue ;
        }
        if(unite(x,y,d-1)) ans++;
    }
    printf("%d\n",ans);
    return 0;
} 

2 种类并查集：

思路：将每一个元素拆成3份，x,x+n,x+2*n。分别表示A,B,C

如果x和y为同类，那么x不能和y+n一组，x不能和y+2*n一组。

如果x吃y的话，那么x不能和y一组，x不能呢y+2*n一组。

code:

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e5+7;
int pre[N+N+N];

int find(int x){
    return pre[x]==x? x:pre[x]=find(pre[x]);
}
void unite(int a,int b){ 
    int x=find(a),y=find(b);
    pre[x]=y;
}

bool same(int x,int y){
    return find(x)==find(y);
}

int main(){
    int n,m;
    cin>>n>>m;
    for(int i=0;i<=n+n+n;i++) pre[i]=i;
    int ans=0;
    for(int i=1;i<=m;i++){
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        y--;z--; 
        if(y>=n||z>=n||y<0||z<0){
            ans++;continue ;
        }
        if(x==1){
            if(same(y,z+n)||same(y,z+2*n)) ans++;
            else {
                unite(y,z);unite(y+n,z+n);unite(y+2*n,z+2*n);
            } 
        }
        else {//如果y吃z的话 
            if(same(y,z)||same(y,z+2*n)) ans++;
            else {
                unite(y,z+n);unite(y+n,z+2*n);unite(y+2*n,z);
            }
        }
    }
    cout<<ans<<endl;
    return 0;
}