How Many Answers Are Wrong HDU - 3038 （经典带权并查集）

题目大意：有一个区间，长度为n，然后跟着m个子区间，每个字区间的格式为x,y,z表示[x,y]的和为z。如果当前区间和与前面的区间和发生冲突，当前区间和会被判错，问：有多少个区间和会被判错。

题解：x,y,z表示从x开始到y的所有数字的和，那么x-1就表示从(x-1,y]的区间和。我们可以对区间的左边x-1寻找他的左端点，同时对区间右边y也寻找他的左端点，如果这两个左端点相等（设为l）那么他就是将区间了[l,y]拆分成了[l,x-1]和[x,y]，我们判断一下区间和是不是相等的就可以了也就是w[y]==w[x-1]+realtion。

如果左端点不相等的话，我们就进行合并。

 

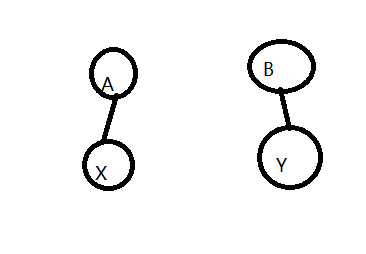
(A和B分别为x和y的根节点)

合并后：

 

 

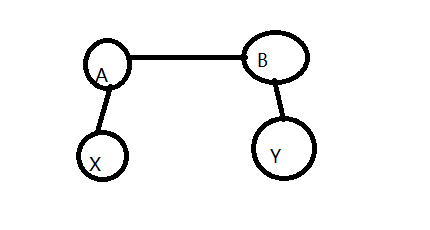
然后再修改权值， 规定B为A的父节点，也就是说现在这棵树B是根节点了，x到B的路径应该有两种，一种是x->A->B，权值之和为w[x]+AB，另外一种是x->y->b权值之和为relation+w[y]

二者应该相等，所以w[x]+AB=relation+w[y]，所以AB=w[A]=w[y]-w[x]+relation。

code:

　　

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+7;
int fa[N];
int w[N];
int find(int x){
    if(x==fa[x]) return x;
    else {
        int c=find(fa[x]);
        w[x]+=w[fa[x]];
        return fa[x]=c;
    }
}
bool unite(int x,int y,int relation){
    int fx=find(x),fy=find(y);
    if(fx!=fy){
        fa[fy]=fx;
        w[fy]=w[x]-w[y]+relation;
        return 0;
    }
    else {
        return relation!=w[y]-w[x];
    }
}
int main(){
    int n,m;
    ios::sync_with_stdio(0);
    while(cin>>n>>m){
        for(int i=0;i<=n;i++) {
            fa[i]=i;
            w[i]=0;
        }
        int ans=0;
        for(int i=1;i<=m;i++){
            int x,y,z;
            cin>>x>>y>>z;
            x--;
            if(unite(x,y,z)) ans++;
        }
        cout<<ans<<endl;
    }
    return 0;
 }