Complete the Sequence HDU - 1121

题目大意：

输入两个数n和m，n表示有n个数，这n个数是一个多项式的前n项，让输出这个序列的n+1，n+2,..n+m项。

题解：差分规律，一直差分，直到全为0或者只剩下一个数。然后再递推回去。

 

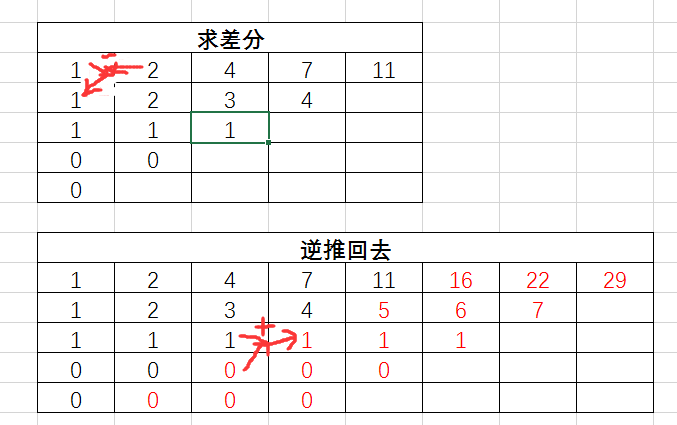
 给出了n个数，最多可以求n-1行差分，从最后一行向上推，共n行。所以总复杂度O(n^2+n*m).

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1E2+7;
ll dp[N][N];
void solve(int t){
//    memset(dp,0,sizeof dp); 
    ll n,c;
    cin>>n>>c;
    for(ll i=1;i<=n;i++) cin>>dp[1][i];
    if(n==1) {
        cout<<dp[1][1];
        for(ll i=2;i<=c;i++) cout<<" "<<dp[1][1]; 
        cout<<endl;
        return ;
    }
    ll pos=2;
    while(1){
        bool flag = false ;
        for(ll i=1;i<=n-pos+1;i++){
            dp[pos][i]=dp[pos-1][i+1]-dp[pos-1][i];
        }
        if(pos==n) break;
        pos++;
    }
    for(ll i=1;i<=c;i++){
        dp[n][i+1]=dp[n][i];
        for(ll j=n-1;j>=1;j--){
            dp[j][n+i+1-j]=dp[j][n+i-j]+dp[j+1][n+i-j];
        }
        if(i==1) cout<<dp[1][n+i];
        else cout<<" "<<dp[1][n+i];
    }
    cout<<endl;
}
int main(){
    ll t;
    cin>>t;
    for(int i=t;i>=1;i--) solve(i);
    return 0;
}