Codeforces Round #613 (Div. 2) A-E简要题解
contest链接:https://codeforces.com/contest/1285
A. Mezo Playing Zoma
签到
1 #include<iostream> 2 #include<vector> 3 #include<cstdio> 4 #include<algorithm> 5 #include<cmath> 6 #include<cstring> 7 #include<queue> 8 #include<map> 9 using namespace std; 10 const int maxn = 205; 11 typedef long long ll; 12 queue<pair<int,int> > q; 13 map<int,bool> vis; 14 vector<int> v; 15 /* 16 1111111111111111111111111111111111111 17 */ 18 int a[maxn]; 19 int main() 20 { 21 int n; 22 cin>>n; 23 string s; 24 cin>>s; 25 int n1=0,n2=0; 26 for(int i=0;i<s.size();i++) 27 { 28 if(s[i]=='L') 29 n1++; 30 if(s[i]=='R') 31 n2++; 32 } 33 cout<<n2+n1+1; 34 return 0; 35 }
B. Just Eat It!
1 #include <bits/stdc++.h> 2 using namespace std; 3 #define finish(x) return cout << x << endl, 0 4 #define ll long long 5 6 int n; 7 vector <int> a; 8 9 bool solve(){ 10 cin >> n; 11 a.resize(n); 12 for(auto &i : a) cin >> i; 13 ll sum = 0; 14 for(int i = 0 ; i < n ; i++){ 15 sum += a[i]; 16 if(sum <= 0) return 0; 17 } 18 sum = 0; 19 for(int i = n - 1 ; i >= 0 ; i--){ 20 sum += a[i]; 21 if(sum <= 0) return 0; 22 } 23 return 1; 24 } 25 int main(){ 26 ios_base::sync_with_stdio(0); 27 cin.tie(0); 28 int T; 29 cin >> T; 30 while(T--){ 31 if(solve()) cout << "YES\n"; 32 else cout << "NO\n"; 33 } 34 }
C. Fadi and LCM
题意:给一个整数X(1~10^12),找到两个数a,b,使得LCM(a,b) = X,且max(a,b)尽可能地小。
思路:LCM(a,b) = X,则a,b必是X的因子,那么对于X,除去他自己本身,最大的因子不会超过√x,且对于X始终会存在一对a,b互素,LCM(a,b) = X。所以枚举a从√x开始,如果再计算n/a = b,若gcd(a,b) = 1,则就是使得max(a,b)尽可能小的答案了。
AC:
1 #include<iostream> 2 #include<vector> 3 #include<cstdio> 4 #include<algorithm> 5 #include<cmath> 6 #include<cstring> 7 #include<queue> 8 #include<map> 9 using namespace std; 10 const int maxn = 205; 11 typedef long long ll; 12 ll gcd(ll a, ll b){ return b?gcd(b,a%b):a; } 13 ll lcm(ll a, ll b){ return a/gcd(a,b)*b; } 14 vector<ll> v1; 15 int main() 16 { 17 ll a,b; 18 ll n; 19 cin>>n; 20 for(int i = sqrt(n);i>=2;i--){ 21 if(n%i == 0){ 22 if(gcd(i,n/i) == 1){ 23 cout<<i<<" "<<n/i; 24 return 0; 25 } 26 } 27 } 28 cout<<1<<" "<<n; 29 return 0; 30 }
D. Dr. Evil Underscores
题意:给n个数a1,a2,a3.....an,找到一个数X,使得X 异或所有的ai ,得到的max(X xor ai)最小,输出这个值。
思路:a的范围是0~230,我们可以以01二进制的形式建一棵深度为30的字典树,每个数ai 的二进制序列插入到字典树中去,例如5 = 101,那么101按位插入到字典树中去。然后从根开始遍历,在字典树上dp,因为该字典树建完后是一棵二叉树,所以分支情况就两种,下一位是0或1,那么如果只遇到1就往1这个分支走,这一位便没有贡献,如果只遇到0就往0这个分支走,这一位也没有贡献,如果遇到的是0和1两个分支,那么必定要加上这一位的贡献,然后递归01两个分支,两者再去min,一直递归到最后一位。
AC代码:
1 #include<iostream> 2 #include<vector> 3 #include<cstdlib> 4 #include<cstdio> 5 #include<algorithm> 6 #include<cmath> 7 #include<cstring> 8 #include<queue> 9 #include<map> 10 using namespace std; 11 typedef long long ll; 12 int trie[6000005][2],cnt ; 13 //bool exist[31*31];// 该结点结尾的字符串是否存在 14 void insert(int a){//建trie树 15 int p = 0; 16 for(int i = 29;i>=0;i--){ 17 int c = (a>>i)&1; 18 if(!trie[p][c]) trie[p][c] = ++cnt; // 如果没有,就添加结点 19 p = trie[p][c]; 20 } 21 // exist[p] = 1; 22 } 23 ll solve(ll cur,int k){ 24 if(k == -1) return 0; 25 if(trie[cur][0] == 0){ 26 return solve(trie[cur][1],k-1);//如果只有1分支 27 } 28 else if(trie[cur][1] == 0){//如果只有0分支 29 return solve(trie[cur][0],k-1); 30 } 31 else{ 32 return (1<<k)+min(solve(trie[cur][0],k-1),solve(trie[cur][1],k-1));//0 1分支都有的情况 33 } 34 } 35 int main() 36 { 37 int n; 38 cin>>n; 39 for(int i = 0;i<n;i++){ 40 ll a;cin>>a; 41 insert(a); 42 } 43 ll ans = solve(0,29); 44 cout<<ans; 45 return 0; 46 }
E. Delete a Segment
题意:给一个数轴上有n个线段集,线段集若有相交,则合并为一个新的合并线段集,比如[1,6]和[2,9],因为两个线段有相交,所以要合并为[1,9],先问删掉给定的n个线段集中的任意一个,剩下的n-1个线段组成的新的合并线段集数量最大是多少?
思路:
这道题首先想到的是并查集做法,枚举删除任意一条线段后,剩下的线段组成的集合是多少,取max,这个复杂度有n2 × 并查集复杂度,显然是不行的。那么考虑离散化处理线段左右端点,然后去扫描。
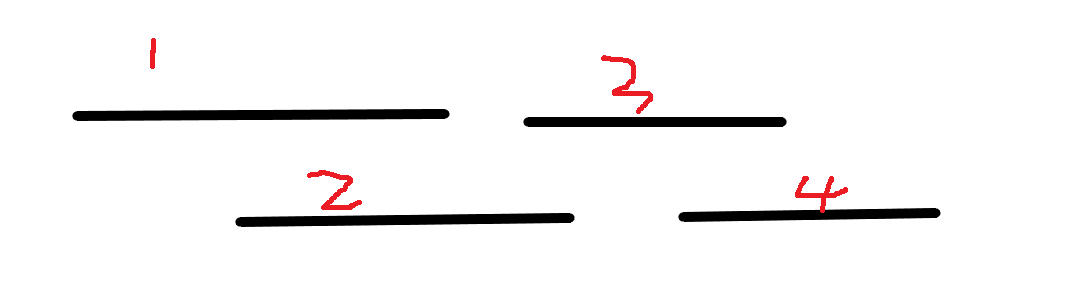
如图所示,线段1,2,3,4离散化处理左右端点,然后排个序并标记一下线段号,开始扫描,扫描到的端点先放入multiset集合中去,最初扫描到线段1的左端点L1,然后是L2,再然后是R1,此时我们发现,线段1已经扫描完比,那么删除这条线段1的左右端点,发现集合中只剩下了L2,且下一个要扫描到的端点是L3,此时就意味着删除点线段2后,线段1和线段3是不相交的,那么删除线段2后,新线段合并集合数量就会+1。同理当扫描到R2时,整个线段2已经扫描完毕,删除集合中线段2左右端点,集合只剩下线段3的左端点,且下一个元素是线段4的左端点,说明线段2和线段4不相交,那么此时删除线段3,就意味着线段2和线段4不相连,新线段合并集合数量就+1,根据以上这个性质,扫描的时候枚举下个元素是左端点还是右端点,记录删除每个线段删除后,合并集合会增加多少,最终拿最初不删除任何线段得到的合并线段集数量+max(删除某一线段增加的数量)就是答案
当然要特判一种情况:
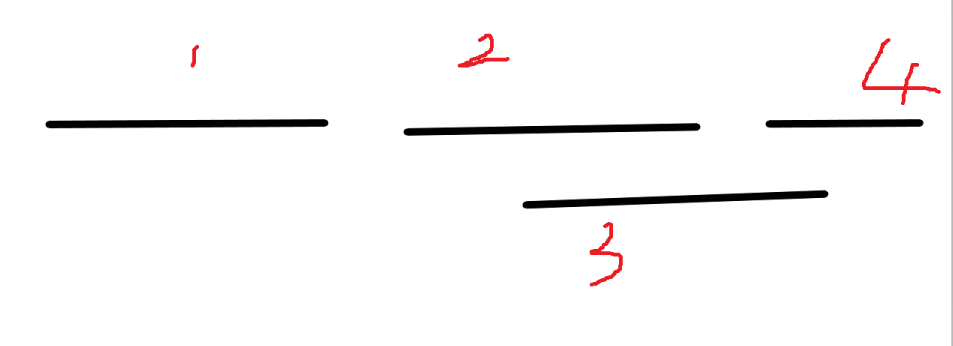
如图所示线段1这种情况,删除这条线段,则新合并集是-1,因为它没有和任何线段有相交,本身就构成一个独立的合并线段集,删除就减少1个合并线段集,特判这种情况即可。
AC代码:
1 #include<iostream> 2 #include<vector> 3 #include<cstdlib> 4 #include<cstdio> 5 #include<algorithm> 6 #include<cmath> 7 #include<set> 8 #include<cstring> 9 #include<queue> 10 #include<map> 11 using namespace std; 12 typedef long long ll; 13 const int maxn = 4e5+10; 14 pair<ll,ll> p[maxn]; 15 int cnt[maxn]; 16 int main() 17 { 18 int t; 19 cin>>t; 20 while(t--){ 21 int n; 22 cin>>n; 23 for(int i = 1;i<=n;i++){ 24 ll l,r; 25 cin>>l>>r; 26 p[2*i-1] = make_pair(l,-i);//离散化记录区间左右端点的位置和区间标号i 27 p[2*i] = make_pair(r,i); 28 cnt[i] = 0; 29 } 30 sort(p+1,p+2*n+1); 31 int ans = 0; 32 multiset<int> s; 33 for(int i = 1;i<=2*n;i++){ 34 if(p[i].second < 0){//如果是左端点,就插入set 35 s.insert(-p[i].second ); 36 } 37 else{ 38 s.erase(s.find(p[i].second));//如果是右端点,就把这个区间删除 39 } 40 if(s.size() == 0) ans++;//如果集合是空,记录一个合并的区间 41 if(s.size() == 1 && p[i].second > 0 && p[i+1].second < 0 && p[i+1].first > p[i].first ){ 42 cnt[*s.begin()]++;//当前是左端点,但是下个是右端点,cnt++ 43 } 44 if(s.size() == 1 && p[i].second < 0 && p[i+1].second >0){ 45 cnt[*s.begin()]--;//特判,如果首先插入地是一段单独区间(l r),去掉这个区间则区间数量-1 46 } 47 } 48 int t = -1; 49 for(int i = 1;i<=n;i++){ 50 t = max(t,cnt[i]); 51 } 52 cout<<ans+t<<endl; 53 } 54 return 0; 55 }


