noip模拟14

A. 队长快跑(leader)

首先考虑到\(n^3\)的动态规划，考虑如何优化..
我们发现，对于当前是否能够选择当前的值，取决与前面的\(A\)，于是考虑如何维护前面的\(A\)值，由此我们可以考虑线段树..
另外本题有一个分类讨论..
正解中用了一个非常巧妙的转换，将\(A\)的值转移到了\(B\)上，从而直接根据Dp转移方程使线段树维护相应的值..

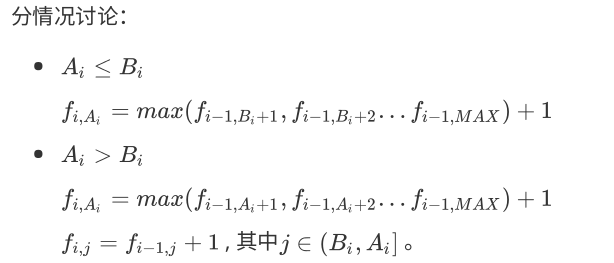
A_code

#include<bits/stdc++.h>
using namespace std;
#define ll long long int
#define lf double
#define mp make_pair
#define lb lower_bound
const ll N=1e6+50;
inline void read(ll &ss)
{
	ss=0; bool cit=0; char ch;
	while(!isdigit(ch=getchar())) if(ch=='-') cit=1;
	while(isdigit(ch)) ss=(ss<<3)+(ss<<1)+(ch^48),ch=getchar();
	if(cit) ss=-ss;
}
ll n,cnt;
ll f[N],a[N],b[N];
ll lsh[N*2];
struct I { ll l,r,sum,maxn,lazy; } tr[N*20];
void spread(ll x)
{
	if(tr[x].lazy)
	{
		tr[x<<1].maxn+=tr[x].lazy;
		tr[(x<<1)|1].maxn+=tr[x].lazy;
		tr[x<<1].lazy+=tr[x].lazy;
		tr[(x<<1)|1].lazy+=tr[x].lazy;
		tr[x].lazy=0;
	}
	return ;
}
void change(ll x,ll pos,ll val)
{
	if(tr[x].l==tr[x].r)
	{
		tr[x].maxn=max(tr[x].maxn,val);
		return ;
	}
	spread(x);
	ll mid=(tr[x].l+tr[x].r)>>1;
	if(pos<=mid) change(x<<1,pos,val);
	else change((x<<1)|1,pos,val);
	tr[x].maxn=max(tr[x<<1].maxn,tr[(x<<1)|1].maxn);
	return ;
}
void update(ll x,ll l,ll r,ll val)
{
	if(l>r) return ;
	if(tr[x].l>=l and tr[x].r<=r)
	{
		tr[x].maxn+=val;
		tr[x].lazy+=val;
		return ;
	}
	spread(x);
	ll mid=(tr[x].l+tr[x].r)>>1;
	if(l<=mid) update(x<<1,l,r,val);
	if(r>=mid+1) update((x<<1)|1,l,r,val);
	tr[x].maxn=max(tr[x<<1].maxn,tr[(x<<1)|1].maxn);
	return ;
}
ll query_max(ll x,ll ql,ll qr)
{ 
	if(ql>qr) return 0;
   	if(tr[x].l>=ql and tr[x].r<=qr) 
	{
		return tr[x].maxn;
	}
	spread(x); ll temp=0;
	ll mid=(tr[x].l+tr[x].r)>>1;
	if(ql<=mid) temp=max(temp,query_max(x<<1,ql,qr));
	if(qr>=mid+1) temp=max(temp,query_max((x<<1)|1,ql,qr));
	return temp;
} 
void build(ll x,ll l,ll r)
{
	tr[x].l=l; tr[x].r=r;
	if(tr[x].l==tr[x].r) return ;
	ll mid=(l+r)>>1;
	build(x<<1,l,mid); build((x<<1)|1,mid+1,r);
	return ;
}
signed main()
{
	read(n);
	for(ll i=1;i<=n;i++)
	{
		read(a[i]); read(b[i]);
		lsh[(i<<1)-1]=a[i]; lsh[i<<1]=b[i];
	}
	sort(lsh+1,lsh+(n<<1)+1); ll ans=0;
	cnt=unique(lsh+1,lsh+1+(n<<1))-lsh-1;
//	for(ll i=1;i<=n;i++)
//	{
//		cout<<lb(lsh+1,lsh+1+cnt,a[i])-lsh<<" ";
//		cout<<lb(lsh+1,lsh+1+cnt,b[i])-lsh<<"\n";	
//	}
	build(1,1,cnt);
	for(ll i=1;i<=n;i++)
	{
		a[i]=lb(lsh+1,lsh+1+cnt,a[i])-lsh;
		b[i]=lb(lsh+1,lsh+1+cnt,b[i])-lsh;	
		if(a[i]<=b[i])
		{
			ans=query_max(1,b[i]+1,cnt)+1;
			change(1,a[i],ans);
		}
		else
		{
			ans=query_max(1,a[i]+1,cnt)+1;
			update(1,b[i]+1,a[i],1);change(1,a[i],ans);
		}
	}
	printf("%lld",query_max(1,1,cnt));
	return 0;
}

B.影魔(shadow)

我们发现这个题目要求维护的东西很多..
对于本题，解决这个问题的方法目前我已知两种，但同样都是使用主席树：
<1> 维护差分答案：
树剖之后，我们可以选择在修改权值时，直接搞一个树上差分即可..
<2> 在每个单点上再去开一棵权值线段树：
我们在维护完不同灵魂种类（以下统称灵魂种类为颜色）的深度之后，再去维护建立在深度上的颜色数..
并且我们在合并的时候，只需要维护同一颜色的最浅深度即可..
因为在合并的时候是不断靠向根节点的，也就是深度逐渐减小，而为了能够让深度小的节点们也能够统计完全，这时就要维护最小的深度..

B_code

#include<bits/stdc++.h>
using namespace std;
#define ll long long int
#define re register ll
#define lf double
#define lb lower_bound
#define mp make_pair
const ll N=1e5+50;
inline void read(ll &ss)
{
	ss=0; bool cit=0; char ch;
	while(!isdigit(ch=getchar())) if(ch=='-') cit=1;
	while(isdigit(ch)) ss=(ss<<3)+(ss<<1)+(ch^48),ch=getchar();
	if(cit) ss=-ss;
}
ll n,m,ts,ans,alls,cnt;
ll sp[N],head[N],lsh[N],dep[N],rt1[N],rt2[N];
bool vis[N];
struct I { ll u,v,nxt; } a[N];
struct II { ll l,r,val; } tr[N*100];
inline void add(ll u,ll v)
{
	a[++ts].u=u;
	a[ts].v=v;
	a[ts].nxt=head[u];
	head[u]=ts;
}
void build(ll &x,ll l,ll r,ll pos,ll val)
{
	if(!x) x=++alls;
	if(l==r) { tr[x].val=val; return ; }
	ll mid=(l+r)>>1;
	if(pos<=mid) build(tr[x].l,l,mid,pos,val);
	else build(tr[x].r,mid+1,r,pos,val);
	return ;
}
void update(ll &x,ll l,ll r,ll pos,ll val)
{
	++alls;
	tr[alls]=tr[x]; x=alls;
	tr[x].val+=val;
	if(l==r) return ;
	ll mid=(l+r)>>1;
	if(pos<=mid) update(tr[x].l,l,mid,pos,val);
	else update(tr[x].r,mid+1,r,pos,val);
	return ;
}
ll merge1(ll x,ll y,ll l,ll r,ll pos)
{
	if(!x) return y; if(!y) return x;
	ll rt=++alls;
	if(l==r) 
	{
		tr[rt].val=min(tr[x].val,tr[y].val);
		update(rt2[pos],1,n,max(tr[x].val,tr[y].val),-1);
		return rt;
	}
	ll mid=(l+r)>>1;
	tr[rt].l=merge1(tr[x].l,tr[y].l,l,mid,pos);
	tr[rt].r=merge1(tr[x].r,tr[y].r,mid+1,r,pos);
	return rt;
}
ll merge2(ll x,ll y,ll l,ll r)
{
	if(!x) return y; if(!y) return x;
	ll rt=++alls;;
	tr[rt].val=tr[x].val+tr[y].val;
	ll mid=(l+r)>>1;
	tr[rt].l=merge2(tr[x].l,tr[y].l,l,mid);
	tr[rt].r=merge2(tr[x].r,tr[y].r,mid+1,r);
	return rt;
}
ll query(ll x,ll l,ll r,ll ql,ll qr)
{
//	cout<<tr[x].l<<" "<<tr[x].r<<" "<<tr[x].val<<endl;
	if(l>=ql and r<=qr) return tr[x].val;
	ll mid=(l+r)>>1; ll temp=0;
	if(ql<=mid) temp+=query(tr[x].l,l,mid,ql,qr);
	if(qr>=mid+1) temp+=query(tr[x].r,mid+1,r,ql,qr);
	return temp;
}
void dfs1(ll now,ll depth)
{
	dep[now]=depth;
	for(ll i=head[now];i;i=a[i].nxt)
		dfs1(a[i].v,depth+1);
	return ;
}
void dfs2(ll now)
{
	build(rt1[now],1,cnt,sp[now],dep[now]);
	update(rt2[now],1,n,dep[now],1);
	for(ll i=head[now];i;i=a[i].nxt)
	{
		dfs2(a[i].v);
		rt1[now]=merge1(rt1[now],rt1[a[i].v],1,cnt,now);
		rt2[now]=merge2(rt2[now],rt2[a[i].v],1,n);
	}
	return ;
}
signed main()
{
	read(n); read(m); ll temp,u,d;
	for(ll i=1;i<=n;i++) { read(sp[i]); lsh[i]=sp[i]; }
	for(ll i=2;i<=n;i++) { read(temp); add(temp,i); }
	sort(lsh+1,lsh+1+n); cnt=unique(lsh+1,lsh+1+n)-lsh-1;
	for(ll i=1;i<=n;i++) sp[i]=lb(lsh+1,lsh+1+cnt,sp[i])-lsh;
	dfs1(1,1); dfs2(1);
	for(ll i=1;i<=m;i++)
	{
		read(u); read(d);
		printf("%lld\n",query(rt2[u],1,n,dep[u],dep[u]+d));
	}
	return 0;
}

C.抛硬币(coin)

S \(\leq\) 3000 ，所以可以考虑\(O(n^2)\)..
Dp个人感觉很奇妙，但是又比较合乎常理且并不是一定想不到..
\(dp_{i,j}\) 表示前 \(i\) 个位置时，长度为 \(j\) 的本质不同的子序列个数..
应用到了一个最简单的容斥..
在一顿推导后我们可以直接得到一个转移方程:

\[dp_{i,j}=dp_{i-1,j}+dp_{i,j-1} \]

但是我们发现会把以第\(i\)个位置的字符\(s\)为结尾的串算重，所以减去就好了..
设 \(pos\) 为\(s\)上次出现的位置..
所以进一步完善得到：

\[dp_{i,j}=dp_{i-1,j}+dp_{i,j-1}-dp_{pos-1,j-1} \]

C_code

#include<bits/stdc++.h>
using namespace std;
#define ll long long int
#define lf double
#define mp make_pair
#define lb lower_bound
const ll N=3e3+50;
const ll mod=998244353;
inline void read(ll &ss)
{
	ss=0; bool cit=0; char ch;
	while(!isdigit(ch=getchar())) if(ch=='-') cit=1;
	while(isdigit(ch)) ss=(ss<<3)+(ss<<1)+(ch^48),ch=getchar();
	if(cit) ss=-ss;
}
ll n,m;
ll f[N][N],s[N];
ll vis[30],lst[N];
signed main()
{
	char ch=getchar();
	while(ch>='a' and ch<='z') 
	{
		s[++n]=ch-'a'+1; ch=getchar();
	}
	read(m);
	for(ll i=1;i<=n;i++)
	{
		if(vis[s[i]]) lst[i]=vis[s[i]],vis[s[i]]=i;
		else vis[s[i]]=i;
	}
	f[0][0]=1;
	for(ll i=1;i<=n;i++)
	{
		f[i][0]=1;
		for(ll j=1;j<=m;j++)
		{
			f[i][j]=(f[i][j]+(f[i-1][j]+f[i-1][j-1])%mod)%mod;
			if(lst[i]) f[i][j]=(f[i][j]-f[lst[i]-1][j-1]+mod)%mod;
		}
	}
	printf("%lld",f[n][m]%mod);
	return 0;
}

经验和教训

考试经常会为了打正解而放弃打暴力..这并不是一个值得肯定的做法..
想正解是永远不会变的，但是我们在打完正解之后也需要使用暴力程序对拍..
所以我们或许可以先码出暴力，顺便我们还可以自己乱造数据..