hdu 6035(树形dp)
题意:给你棵树,树上每个节点都有颜色,每条路径上有m种颜色 问你所有路径上出现的颜色的和
思路:答案求的是每种颜色对路径的贡献 我们可以反过来每种颜色不经过的路径的条数
假设根节点的颜色为x 我们就可以知道不过x颜色的路径一定不经过这个根节点 和不经过这个子树中颜色为x的节点
所有树形dp。。。。。。。
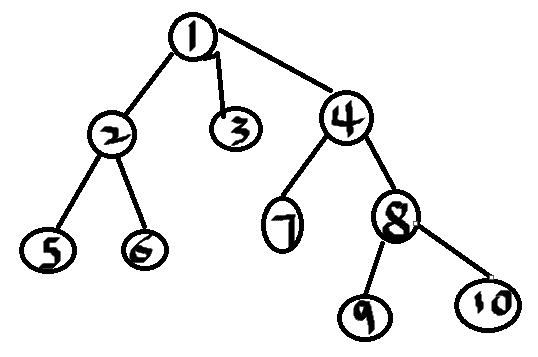
son[u]统计的是以u的根节点的子树的大小 节点的颜色为a[i] sum[a[i]]为在以i节点为根节点颜色a[i]的子树大小, 比如 1 8节点的颜色相同 x颜色没有经过的节点为1的儿子-sum[a[8]];
sum[a[8]]是可以在DFS中过程得到的 没有经过的点有y个 路径就有y*(y-1)/2;
所有我们在DFS一遍就能求出所有颜色没有经过的路径数目
答案就是所有的颜色经过所有的路径-所有的点没有经过的路径数目
我感觉dfs解释的有点牵强 具体看代码把 比较好理解
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cstdlib> 6 #include<string.h> 7 #include<set> 8 #include<vector> 9 #include<queue> 10 #include<stack> 11 #include<map> 12 #include<cmath> 13 typedef long long ll; 14 typedef unsigned long long LL; 15 using namespace std; 16 const double PI=acos(-1.0); 17 const double eps=0.0000000001; 18 const int N=500000+100; 19 int a[N],b[N]; 20 int n,m; 21 int tot; 22 int head[N]; 23 ll ans; 24 int son[N]; 25 int sum[N]; 26 struct node{ 27 int to,next; 28 }edge[N<<1]; 29 void init(){ 30 memset(head,-1,sizeof(head)); 31 memset(sum,0,sizeof(sum)); 32 tot=0; 33 } 34 void add(int u,int v){ 35 edge[tot].to=v; 36 edge[tot].next=head[u]; 37 head[u]=tot++; 38 } 39 void DFS(int u,int fa){ 40 son[u]=1; 41 ll t=sum[a[u]]; 42 ll c=0; 43 for(int i=head[u];i!=-1;i=edge[i].next){ 44 int v=edge[i].to; 45 if(v==fa)continue; 46 DFS(v,u); 47 son[u]=son[v]+son[u]; 48 ll temp=son[v]-(sum[a[u]]-t); 49 t=sum[a[u]]; 50 c=c+temp; 51 ans=ans-(temp-1)*temp/2; 52 } 53 sum[a[u]]+=c+1; 54 } 55 int main(){ 56 int tt=1; 57 while(scanf("%d",&n)!=EOF){ 58 init(); 59 for(int i=1;i<=n;i++)scanf("%d",&a[i]); 60 for(int i=1;i<n;i++){ 61 int u,v; 62 scanf("%d%d",&u,&v); 63 add(u,v); 64 add(v,u); 65 } 66 ans=(ll)n*(n-1)*n/2; 67 DFS(1,0); 68 for(int i=1;i<=n;i++){ 69 ll temp=n-sum[i]; 70 ans=ans-(temp-1)*temp/2; 71 } 72 printf("Case #%d: %lld\n", tt++, ans); 73 } 74 }


