CodeForces - 557D Vitaly and Cycle(二分图)
Vitaly and Cycle
After Vitaly was expelled from the university, he became interested in the graph theory.
Vitaly especially liked the cycles of an odd length in which each vertex occurs at most once.
Vitaly was wondering how to solve the following problem. You are given an undirected graph consisting of n vertices and m edges, not necessarily connected, without parallel edges and loops. You need to find t — the minimum number of edges that must be added to the given graph in order to form a simple cycle of an odd length, consisting of more than one vertex. Moreover, he must find w — the number of ways to add t edges in order to form a cycle of an odd length (consisting of more than one vertex). It is prohibited to add loops or parallel edges.
Two ways to add edges to the graph are considered equal if they have the same sets of added edges.
Since Vitaly does not study at the university, he asked you to help him with this task.
The first line of the input contains two integers n and m (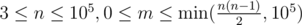 — the number of vertices in the graph and the number of edges in the graph.
— the number of vertices in the graph and the number of edges in the graph.
Next m lines contain the descriptions of the edges of the graph, one edge per line. Each edge is given by a pair of integers ai, bi (1 ≤ ai, bi ≤ n) — the vertices that are connected by the i-th edge. All numbers in the lines are separated by a single space.
It is guaranteed that the given graph doesn't contain any loops and parallel edges. The graph isn't necessarily connected.
Print in the first line of the output two space-separated integers t and w — the minimum number of edges that should be added to the graph to form a simple cycle of an odd length consisting of more than one vertex where each vertex occurs at most once, and the number of ways to do this.
4 4
1 2
1 3
4 2
4 3
1 2
3 3
1 2
2 3
3 1
0 1
3 0
3 1
The simple cycle is a cycle that doesn't contain any vertex twice.
题意:给你一个n个节点m条边的图 问你是不是存在一个奇数环(就是环中的节点个数为奇数个)
如果存在输出0 1
如果不存在 输出最少加多少条边使得存在一个奇数环 并输出他的方案数
当一个图是二分图的话 他是一定不存在奇数环的 反之 他就一定存在奇数环
0 1染色判断是不是二分图
如果是二分图的话 也许是多个联通块 所以我们只需要统计各个联通块中0 1中的个数 a[i] b[i] 答案就是各个联通块的 a(a-1)/2+b(b-1)/2的和
当然 有两种情况是要讨论的 m=0 不存在边 所以就是任意三个点可以组成一个奇数环 边就是加3条
还是一种已经所有联通块中节点数最多就只有两个 答案就是 (n-2)*m
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cstdlib> 6 #include<string.h> 7 #include<set> 8 #include<vector> 9 #include<queue> 10 #include<stack> 11 #include<map> 12 #include<cmath> 13 typedef long long ll; 14 typedef unsigned long long LL; 15 using namespace std; 16 const double PI=acos(-1.0); 17 const double eps=0.0000000001; 18 const int N=100000+100; 19 int head[N]; 20 int tot; 21 struct node{ 22 int to,next; 23 }edge[N<<1]; 24 int color[N]; 25 int vis[N]; 26 int a[N]; 27 int b[N]; 28 int num[N]; 29 void init(){ 30 memset(head,-1,sizeof(head)); 31 tot=0; 32 } 33 void add(int u,int v){ 34 edge[tot].to=v; 35 edge[tot].next=head[u]; 36 head[u]=tot++; 37 } 38 int DFS(int u,int t){ 39 if(vis[u]==0){ 40 if(color[u]==0)a[t]++; 41 if(color[u]==1)b[t]++; 42 num[t]++; 43 } 44 vis[u]=1; 45 for(int i=head[u];i!=-1;i=edge[i].next){ 46 int v=edge[i].to; 47 if(color[v]==0){ 48 color[v]=color[u]^1; 49 if(DFS(v,t)==0)return 0; 50 } 51 else if(color[u]==color[v]){ 52 return 0; 53 } 54 } 55 return 1; 56 } 57 int main(){ 58 int n,m; 59 scanf("%d%d",&n,&m); 60 init(); 61 int u,v; 62 for(int i=1;i<=m;i++){ 63 scanf("%d%d",&u,&v); 64 add(u,v); 65 add(v,u); 66 } 67 if(m==0){ 68 cout<<3<<" "<<(ll)n*(n-1)*(n-2)/6<<endl;return 0; 69 } 70 memset(color,0,sizeof(color)); 71 memset(vis,0,sizeof(vis)); 72 int flag=0; 73 int t=0; 74 for(int i=1;i<=n;i++){ 75 if(color[i]==0&&vis[i]==0){ 76 if(DFS(i,++t)==0){ 77 color[i]=0; 78 flag=1; 79 break; 80 } 81 } 82 }/* 83 for(int i=1;i<=n;i++){ 84 cout<<color[i]<<" "<<endl; 85 } 86 for(int i=1;i<=t;i++){ 87 cout<<a[i]<<" "<<b[i]<<" "<<num[i]<<endl; 88 }*/ 89 if(flag==1){ 90 cout<<0<<" "<<1<<endl;return 0; 91 } 92 ll ans=0; 93 flag=0; 94 for(int i=1;i<=t;i++){ 95 if(num[i]<=2){ 96 flag++;continue; 97 } 98 ans=ans+(ll)a[i]*(a[i]-1)/2+(ll)b[i]*(b[i]-1)/2; 99 //cout<<ans<<endl; 100 } 101 if(flag!=t)cout<<1<<" "<<ans<<endl; 102 else{ 103 cout<<2<<" "<<(ll)m*(n-2)<<endl; 104 } 105 106 }

