网络流之最大流算法(EK算法和Dinc算法)
最大流
网络流的定义:
在一个网络(有流量)中有两个特殊的点,一个是网络的源点(s),流量只出不进,一个是网络的汇点(t),流量只进不出。
最大流:就是求s-->t的最大流量
假设 u,v 两个点,连接这两个点的边为e(u,v);
对于每一条边都有一个实际流量f(u,v),还有一个容量c(u,v),就是这条边上可以通过的最大流量。
当一条边的容量c(u,v)=0,证明这条边是不存在的,
作为一个合格的网络流,必须满足三个条件:
1>每条边的实际流量小于等于容量 f(u,v)<=c(u,v);
2>f(u,v)=-f(v,u);
3>对于不是源点和汇点的点,流入的流量等于流出的流量
如何来求一个网络的最大流:
如图是一个网路流,很明显看出答案是4。
我们要求s-t的流量,我们可以选择这样来求解,我们先从s点出发,找到一条s-t的路径,记录这条路径上那个最小的实际流量,
算法就是我们要找到很多条这样的路径,但这些路径都应该是不同的,所有我们只需要把这多条路径的的最小流量相加 得到就是最大流、
这个寻找s-t的路径也叫做增广路算法。
其实这里困难的就是如何保证这些路径是不会相同的 这是涉及到一个概念 就是残留网络
残留网络就是每次利用增广路算法找到这条路径的最小实际流量 minn,我们在原网络中把这条边的容量都减去minn,所以必定这条路径中一定会有流量为0。
所有下次增广的话,就一定不会走原路 因为这条路径中有边的流量有0,走是没有意义的。一直到不能增广为止,得到的和就是最大流
如上图 我们可以很好的求出最大流
先增广 找到 s-1-t 这条路 minn=2 所以他的残留网络图变为
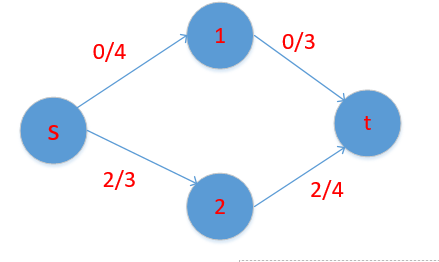
继续增广,得的残留网络为:

这样很容易求到最大流,但这种其实是错误的,比如我们换一个图

假设我们先增广 s-1-2-t, 其实我们就只不在增广了,结果等于2,其实这答案是4,这里就要体现反向边的作用了
我们最开始设的 反向边的值都是0的,就是我们在每次增广后的残流网络不仅边的流量要减去minn,反向弧的流量应该加上minn
比如 ,你先增广s-1-2-t 残留网络为
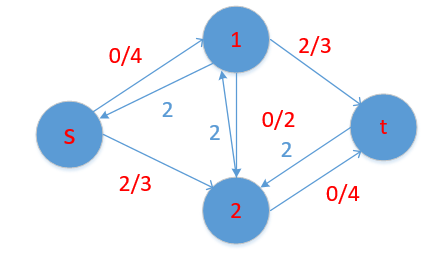
这样我们依然可以继续增广,最终可以得到答案为4
就是给了一个反悔的机会,就是比如我有这条的反向边我依然不能增广,哪这就是无所谓的额,
当我们第二次的增广路走2-1这条反向边的时候,就相当于把1-2这条正向边已经是用了的流量给”退”了回去,不走1-2这条路,而改走从1点出发的其他的路也就是1-t。 (有人问如果这里没有1-t怎么办,这时假如没有1-t这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点)
同时本来在2-t上的流量由s-2-t这条路来”接管”.
这是就网络流最大流中最简单的一个EK算法了(全名不记得了)
下面给出一道入门题 hdu 3549
Flow Problem
Time Limit: 5000/5000 MS (Java/Others) Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 16416 Accepted Submission(s): 7747
For each test case, the first line contains two integers N and M, denoting the number of vertexes and edges in the graph. (2 <= N <= 15, 0 <= M <= 1000)
Next M lines, each line contains three integers X, Y and C, there is an edge from X to Y and the capacity of it is C. (1 <= X, Y <= N, 1 <= C <= 1000)
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cstdlib> 6 #include<string.h> 7 #include<set> 8 #include<vector> 9 #include<queue> 10 #include<stack> 11 #include<map> 12 #include<cmath> 13 typedef long long ll; 14 typedef unsigned long long LL; 15 using namespace std; 16 const double PI=acos(-1.0); 17 const double eps=0.0000000001; 18 const int INF=1e9; 19 const int N=1000+100; 20 int mp[N][N]; 21 int vis[N]; 22 int pre[N]; 23 int m,n; 24 int BFS(int s,int t){ 25 queue<int>q; 26 memset(pre,-1,sizeof(pre)); 27 memset(vis,0,sizeof(vis)); 28 pre[s]=0; 29 vis[s]=1; 30 q.push(s); 31 while(!q.empty()){ 32 int p=q.front(); 33 q.pop(); 34 for(int i=1;i<=m;i++){ 35 if(mp[p][i]>0&&vis[i]==0){ 36 pre[i]=p; 37 vis[i]=1; 38 if(i==t)return 1; 39 q.push(i); 40 } 41 } 42 } 43 return false; 44 } 45 int EK(int s,int t){ 46 int flow=0; 47 //cout<<BFS(s,t)<<endl; 48 while(BFS(s,t)){ 49 //BFS(s,t); 50 int dis=INF; 51 for(int i=t;i!=s;i=pre[i]) 52 dis=min(mp[pre[i]][i],dis); 53 for(int i=t;i!=s;i=pre[i]){ 54 mp[pre[i]][i]=mp[pre[i]][i]-dis; 55 mp[i][pre[i]]=mp[i][pre[i]]+dis; 56 } 57 flow=flow+dis; 58 } 59 return flow; 60 } 61 int main(){ 62 int Case; 63 cin>>Case; 64 int tt=1; 65 while(Case--){ 66 scanf("%d%d",&m,&n); 67 memset(mp,0,sizeof(mp)); 68 for(int i=0;i<n;i++){ 69 int u,v,w; 70 scanf("%d%d%d",&u,&v,&w); 71 mp[u][v]=w+mp[u][v]; 72 // mp[v][u]=0; 73 } 74 int ans=EK(1,m); 75 cout<<"Case "<<tt++<<":"<<" "; 76 cout<<ans<<endl; 77 } 78 79 }
由于EK算法容易超时 所有这个在比赛中不怎么用 所以我们就需要复杂度低的 接下来我们就介绍Dinc算法
其实Dinc算法和EK是很相似的,Dinc中有一个概念 叫做层次图,就是这个使其复杂度低了很多的,主要就是一个多路增广,
就是在BFS一遍的过程中都达到多路增广,而减少复杂度
如下图

Dinc的写法 也是一个板子
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cstdlib> 6 #include<string.h> 7 #include<set> 8 #include<vector> 9 #include<queue> 10 #include<stack> 11 #include<map> 12 #include<cmath> 13 typedef long long ll; 14 typedef unsigned long long LL; 15 using namespace std; 16 const double PI=acos(-1.0); 17 const double eps=0.0000000001; 18 const int INF=1e9; 19 const int N=10000+100; 20 int head[N]; 21 int dis[N]; 22 int tot; 23 int n,m; 24 struct node{ 25 int to,next,flow; 26 }edge[N<<1]; 27 void init(){ 28 memset(head,-1,sizeof(head)); 29 tot=0; 30 } 31 void add(int u,int v,int c){ 32 edge[tot].to=v; 33 edge[tot].flow=c; 34 edge[tot].next=head[u]; 35 head[u]=tot++; 36 } 37 int BFS(int s,int t){ 38 queue<int>q; 39 memset(dis,-1,sizeof(dis)); 40 q.push(s); 41 dis[s]=0; 42 while(!q.empty()){ 43 int x=q.front(); 44 q.pop(); 45 if(x==t)return 1; 46 for(int i=head[x];i!=-1;i=edge[i].next){ 47 int v=edge[i].to; 48 if(edge[i].flow&&dis[v]==-1){ 49 dis[v]=dis[x]+1; 50 q.push(v); 51 } 52 } 53 } 54 if(dis[t]==-1)return 0; 55 else 56 return 1; 57 } 58 int DFS(int s,int flow){ 59 if(s==m)return flow; 60 int ans=0; 61 for(int i=head[s];i!=-1;i=edge[i].next){ 62 int v=edge[i].to; 63 if(edge[i].flow&&dis[v]==dis[s]+1){ 64 int f=DFS(v,min(flow-ans,edge[i].flow)); 65 edge[i].flow-=f; 66 edge[i^1].flow+=f; 67 ans+=f; 68 if(ans==flow)return ans; 69 } 70 } 71 return ans; 72 } 73 int Dinc(int s,int t){ 74 int flow=0; 75 while(BFS(s,t)){ 76 flow+=DFS(s,INF); 77 } 78 return flow; 79 } 80 int main(){ 81 int Case; 82 scanf("%d",&Case); 83 int tt=1; 84 while(Case--){ 85 init(); 86 scanf("%d%d",&m,&n); 87 for(int i=0;i<n;i++){ 88 int u,v,w; 89 scanf("%d%d%d",&u,&v,&w); 90 add(u,v,w); 91 add(v,u,0); 92 // mp[v][u]=0; 93 } 94 int ans=Dinc(1,m); 95 cout<<"Case "<<tt++<<":"<<" "; 96 cout<<ans<<endl; 97 } 98 99 }


