Description
Solution
首先由于 \(\rm dilworth\) 定理可知,一个偏序集的最长反链大小等于其 最小不可重链覆盖 大小。其中最小不可重链覆盖就是在偏序集中选出若干条链,经过每个点至少一次且链数最少的链覆盖。可以发现,在 dag 上做一个传递闭包就可以得到一个偏序集,下文就在这个偏序集上讨论。
考虑用二分图最大匹配构造二分图最大独立集。假设我们已经得出了这样一组匹配(最大匹配数 \(m=4\)):
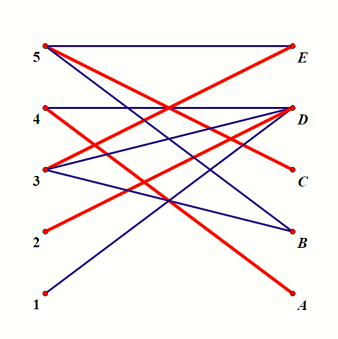
考虑这样一种构造:从右侧的 非匹配点(图示为 \(\rm B\))开始 dfs,右侧的点只能走 非匹配边 向左访问,左侧的点只能走 匹配边 向右访问,如图所示:
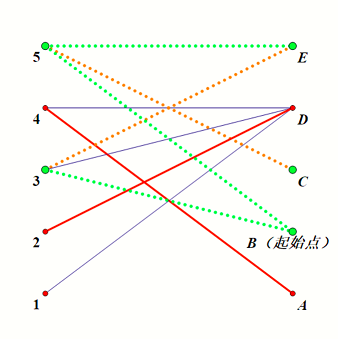
我们遍历到了 \(3,5,\text{B,C,E}\),可以证明,左侧被 dfs 到的点和右侧未被 dfs 到的点组成的点集 \(S\) 是一个最小点覆盖。首先,左侧被 dfs 到的点一定被匹配边覆盖,如果不是就形成了一条交错路,与最大匹配的先提条件相悖。于是右侧未被 dfs 到的点也一定被匹配边覆盖,否则也会形成交错路。综上,左侧被 dfs 到的点和右侧未被 dfs 到的点组成的点集 \(S\) 覆盖了所有匹配边,是一个最小点覆盖。
由于删去最小点覆盖后,剩下的点就是相互独立(不存在一条边的两个端点都不在最小点覆盖)且最多的。所以取最小点覆盖的补集就可以得到最大独立集,也就是 \(1,2,4,\text{B,C,E}\).
令最大独立集为 \(\scr I\),选出所有入点和出点都属于 \(\scr I\) 的点加入点集 \(\scr A\),集合 \(\scr A\) 中的点构成最长反链(显然集合 \(\scr A\) 中的点构成反链,因为任意 \(i,j\in \scr A\),\(i,j\) 的出点入点都没有偏序关系,也就是偏序集上的边)。
考虑证明。由于最小不可重链覆盖实际上就是 原图 总点数减去最大匹配数,所以得到最长反链大小为 \(n-m\),我们只需要证明集合 \(\scr A\) 的大小等于或大于等于 \(n-m\) 即可证明上文结论。
由于 \(|{\scr I}|=2n-|S|=2n-m\),所以也可以证明 \(|{\scr I}|-|{\scr A}|\leqslant n\) 成立。考察 \(|{\scr I}|-|{\scr A}|\) 的意义,实际上就是将所有点分为三类:入点出点均属于 \(\scr I\);入点出点只有一个点属于 \(\scr I\);入点出点均不属于 \(\scr I\)。所以 \(|{\scr I}|-|{\scr A}|\) 实际上就是有多少个点,存在 入点出点中的一个或两个属于 \(\scr I\),也就是前两类点的数量,显然这个量是 \(\leqslant n\) 的。证毕。
至此,我们已经可以用 \(\rm dinic\) 等算法构造出 dag 的最长反链,那么如何判断一个点是否可能在最长反链上呢?考虑一种暴力的方法,枚举每个点并假定其在最长反链上,删除和它有偏序关系的点,因为求解独立集一定不能选取这些点了。再跑一个最大独立集,如果算出的最长反链是删除前减一即合法,复杂度 \(\mathcal O(n^3)\).
Code
# include <cstdio>
# include <cctype>
# define print(x,y) write(x), putchar(y)
template <class T>
inline T read(const T sample) {
T x=0; char s; bool f=0;
while(!isdigit(s=getchar())) f|=(s=='-');
for(; isdigit(s); s=getchar()) x=(x<<1)+(x<<3)+(s^48);
return f? -x: x;
}
template <class T>
inline void write(T x) {
static int writ[50], w_tp=0;
if(x<0) putchar('-'), x=-x;
do writ[++w_tp]=x-x/10*10, x/=10; while(x);
while(putchar(writ[w_tp--]^48), w_tp);
}
# include <queue>
# include <cstring>
# include <iostream>
using namespace std;
const int maxn = 205;
const int infty = 0x3f3f3f3f;
queue <int> q; bool vis[maxn];
bool g[maxn][maxn]; int dep[maxn];
int n, m, head[maxn], cnt=-1, S, T, arc[maxn];
struct edge { int nxt,to,w; } e[int(1e5)];
void addEdge(int u,int v,int w) {
e[++cnt].to=v, e[cnt].nxt=head[u],
e[cnt].w=w, head[u]=cnt;
e[++cnt].to=u, e[cnt].nxt=head[v],
e[cnt].w=0, head[v]=cnt;
}
bool bfs() {
for(int i=1;i<=T;++i)
dep[i]=infty, arc[i]=-1;
while(!q.empty()) q.pop(); int v;
q.push(S), arc[S]=head[S], dep[S]=0;
while(!q.empty()) {
int u=q.front(); q.pop();
for(int i=head[u]; ~i; i=e[i].nxt)
if(e[i].w && dep[v=e[i].to]==infty) {
dep[v] = dep[u]+1,
arc[v]=head[v], q.push(v);
if(v==T) return true;
}
} return false;
}
int dfs(int u,int canFlow) {
if(u==T) return canFlow;
int sumFlow=0, d, v;
for(int i=arc[u]; ~i; i=e[i].nxt) {
arc[u] = i;
if(e[i].w && dep[v=e[i].to]==dep[u]+1) {
d = dfs(v, min(canFlow,e[i].w));
if(!d) dep[v] = infty;
e[i].w -= d, e[i^1].w += d,
canFlow -= d, sumFlow += d;
if(!canFlow) break;
}
} return sumFlow;
}
int dinic() {
int ret=0; while(bfs())
ret+=dfs(S,infty); return ret;
}
void findS(int u) {
if(vis[u]) return; vis[u]=1;
for(int i=head[u]; ~i; i=e[i].nxt)
if(!e[i].w && e[i].to!=T) findS(e[i].to);
}
bool inside(int u) {
return !vis[u+n] && vis[u];
}
int main() {
n=read(9), m=read(9); S=(n<<1)+1, T=S+1;
memset(head,-1,sizeof(int)*(T+2));
for(int i=1;i<=m;++i) {
int u=read(9), v=read(9);
g[u][v] = 1;
}
for(int k=1;k<=n;++k) for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j) g[i][j] |= (g[i][k]&g[k][j]);
for(int i=1;i<=n;++i)
addEdge(S,i+n,1), addEdge(i,T,1);
for(int i=1;i<=n;++i) for(int j=1;j<=n;++j)
if(g[i][j]) addEdge(i+n,j,1);
int M = dinic(); print(n-M,'\n');
for(int i=1;i<=n;++i) if(!vis[i])
if(e[(i<<2)-2].w) findS(i); int all;
for(int i=1;i<=n;++i) write(inside(i)); puts("");
for(int i=1;i<=n;++i) {
for(int j=1;j<=n;++j) vis[j]=0; vis[i]=1;
for(int j=1;j<=n;++j)
if(g[i][j] || g[j][i]) vis[j]=1;
memset(head,-1,sizeof(int)*(T+2)), cnt=-1, all=0;
for(int j=1;j<=n;++j) if(!vis[j])
addEdge(S,j+n,1), addEdge(j,T,1), ++all;
for(int j=1;j<=n;++j) if(!vis[j])
for(int k=1;k<=n;++k) if(!vis[k])
if(g[j][k]) addEdge(j+n,k,1);
if(all-dinic()==n-M-1) putchar('1');
else putchar('0');
} puts("");
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号