Description
Solution
看了提示之后,我们发现每个数在交换时都必须向目标方向走。所以如果存在一个数,它前面有比它大的数,后面有比它小的数就一定不合法,即要求不存在长度超过 \(2\) 的下降子序列。
根据 \(\textrm{dilworth}\) 定理,最长下降子序列的长度不超过 \(2\),即整个排列最少被划分成 \(2\) 的上升子序列数量不能超过 \(2\).
先不考虑字典序限制,记 \(f(i,j)\) 为前 \(i\) 个数的最大值为 \(j\),后面 \(n-i\) 个位置合法的方案数(注意 只计算了后面位置的方案)。考虑第 \(i+1\) 个数填啥,如果填 \(k>j\),那么一定合法;如果填 \(k<j\),那么一定要填当前还没有填的最小值 \(\rm val\),否则序列会出现 \(j>k>\rm val\) 状物,上升子序列个数一定超过 \(2\)。所以有 \(f(i,j)\leftarrow \sum_{k=j}^{n}f(i+1,k)\).
事实上,这个递推式可以用图像来表示
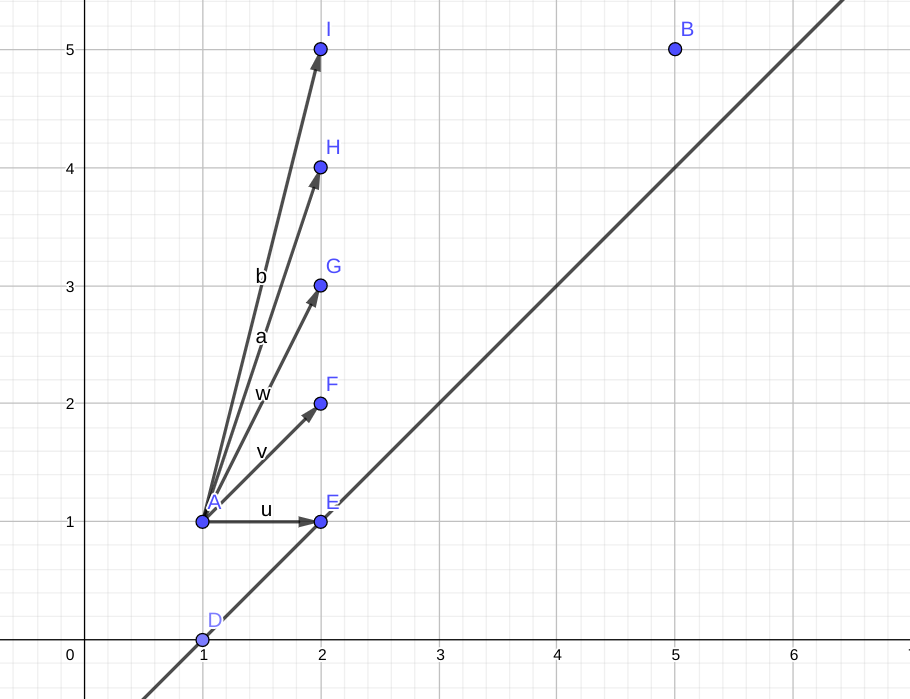
对于 \(n=7\) 且求解 \(f(1,1)\) 的情况,实际上就是从 \(A\) 点出发到达 \(B\) 点且不到达 \(y=x-1\) 这条直线的方案数。先考虑没有直线限制的情况,实际上就是一共走 \(n-i\) 次,每次向右走一步,向上走 \(x(x\geqslant 0)\) 步,且 \(n-j=\sum x\)。用插板法可以算出方案数为 \(\binom{2n-i-j-1}{n-i-1}\).
实际上,这和卡特兰数非常相似。可怜的\(\require{enclose}\enclose{horizontalstrike}{\sf{Oxide}}\)在这个地方卡了好久。看上去这是一个一次操作包含 "每次向右走一步,向上走 \(x(x\geqslant 0)\) 步" 的模型,实际上画画图就可以发现,由于 \(x\) 可以等于零,它的方案数与 "每次向上或向右走一步,第一步必须向右走" 的方案数是等价的!从这个角度,我们也可以理解为啥没有限制的方案数为 \(\binom{2n-i-j-1}{n-i-1}\),因为第一步是固定的。
现在考虑加上限制。模仿卡特兰数的推导,我们直接将 \((n,n)\) 沿 \(y=x-1\) 对称到 \((n+1,n-1)\),然后计算从 \((i,j)\) 开始,第一步向右走,到 \((n+1,n-1)\) 的方案数……吗?事实上这是有问题的,当第一次走到 \(y=x-1\) 上时,这样计算会将下一步向上走 \(x(x>0)\) 步的情况算入,而由于原本操作就是向右走与向上走的复合,所以这种情况点实际并没有走到 \(y=x-1\) 上。如何解决呢?强制第一次走到 \(y=x-1\) 上时再向右走一步即可。那么可以发现这就是走到 \(y=x-2\) 这条直线上,于是不合法的方案数是从 \((i,j)\) 开始,第一步向右走,到 \((n+2,n-2)\) 的方案数,也就是 \(\binom{2n-i-j-1}{n-i+1}\).
继续考虑字典序限制。按位枚举,若当前枚举到第 \(i\) 项,就是计算前 \(i-1\) 项与 \(\{q\}\) 相同,第 \(i\) 项大于 \(q_i\) 的方案数。
记 \(\lim=\max_{j=1}^{i-1}q_j\),\({\rm val}\) 为当前还没有填的最小值。由于 \({\rm val}\) 为当前还没有填的最小值,所以 \(q_i\geqslant \rm val\),于是肯定填不了 \(\rm val\)。将 \(q_i\) 与 \(\lim\) 取 \(\max\),记答案为 \(r\),那么方案数就是 \(\sum_{k=r+1}^n f(i,k)\),这个玩意就是 \(f(i-1,r+1)\),根据上文的推导,可以用组合数 \(\mathcal O(1)\) 地计算。于是总复杂度为 \(\mathcal O(nT)\).
另外字典序还有一个需要注意的地方是,由于钦定前 \(i-1\) 项与 \(\{q\}\) 相同,所以为了维护 "整个排列最少被划分成 \(2\) 的上升子序列数量不能超过 \(2\)" 这个条件,仅仅保证选 \(\rm val\) 或选 \(k>\rm lim\) 的策略是不够的。考虑如果发生 \({\rm val}<q_i<\lim\),那么就会产生 \(\{\lim,q_i,{\rm val}\}\) 的子序列,那么从 \(i+1\) 开始,所有方案都不可能合法了。
Code
# include <cstdio>
# include <cctype>
# define print(x,y) write(x), putchar(y)
template <class T>
inline T read(const T sample) {
T x=0; char s; bool f=0;
while(!isdigit(s=getchar())) f|=(s=='-');
for(; isdigit(s); s=getchar()) x=(x<<1)+(x<<3)+(s^48);
return f? -x: x;
}
template <class T>
inline void write(T x) {
static int writ[50], w_tp=0;
if(x<0) putchar('-'), x=-x;
do writ[++w_tp]=x-x/10*10, x/=10; while(x);
while(putchar(writ[w_tp--]^48), w_tp);
}
# include <cstring>
# include <iostream>
using namespace std;
const int maxn = 1200005;
const int mod = 998244353;
int inv(int x,int y=mod-2,int r=1) {
for(; y; y>>=1, x=1ll*x*x%mod)
if(y&1) r=1ll*r*x%mod; return r;
}
int dec(int x,int y) { return x-y<0?x-y+mod:x-y; }
int inc(int x,int y) { return x+y>=mod?x+y-mod:x+y; }
bool vis[maxn];
int n,fac[maxn],ifac[maxn];
void initialize() { fac[0]=1;
for(int i=1;i<=maxn-5;++i)
fac[i] = 1ll*fac[i-1]*i%mod;
ifac[maxn-5] = inv(fac[maxn-5]);
for(int i=maxn-6;i>=0;--i)
ifac[i] = 1ll*ifac[i+1]*(i+1)%mod;
}
int C(int n,int m) {
if(m<0 || n<m) return 0;
return 1ll*fac[n]*ifac[m]%mod*ifac[n-m]%mod;
}
int f(int i,int j) { return dec(
C(n*2-i-j-1,n-i-1), C(n*2-i-j-1,n-i+1)
); }
void CandyMyWife() {
bool judge = false;
n=read(9); int lim=0, ans=0, val=1;
memset(vis,0,sizeof(bool)*(n+2));
for(int i=1;i<=n;++i) {
int x=read(9); if(judge) continue;
ans = inc(ans,f(i-1,max(lim,x)+1));
if(val<x && x<lim) judge = true;
lim = max(lim,x); vis[x] = true;
while(vis[val]) ++ val;
} print(ans,'\n');
}
int main() {
initialize();
for(int T=read(9); T; --T) CandyMyWife();
return 0;
}
