0. 前置芝士

0.1. 复数

0.1.1. 定义

形如 \(z=a+bi\)（\(a,b\) 均为实数）的数称为复数，其中 \(a\) 称为实部，\(b\) 称为虚部。其中 \(i\) 是虚数单位，满足 \(i^2=-1\).

另外，可以将其想象成平面直角坐标系上的点/向量 \((a,b)\).

定义 \(\theta\) 为复数 \(z\) 的辐角，\(r=\sqrt{a^2+b^2}\) 是模长。那么 \(z\) 可以表示为 \(r\times (\cos \theta+i\sin \theta)\)（显然 \(r\times \cos \theta\) 就是 \(a\)）。

还可以用欧拉公式（\(e^{xi}=\cos x+i\sin x\)）表示：\(z=r\times e^{\theta i}\)。

不过下文就会省略 \(r\)（因为是单位圆）。

0.1.2. 计算

相加/减就是实部与虚部相加/减。

相乘就是 \(z_1z_2=r_1\times r_2\times e^{(x+y)i}\)，即 模长相乘，幅角相加。

由此可见，如果想让复数转动一定角度，我们只用乘上此角度对应的 单位复数 以保障模长不变。

0.2. 多项式表示法

0.2.1. 系数多项式

\[f(x)=\sum_{i=0}^{n-1}a_ix^i \]

0.2.2. 点值多项式

选取 \(n\) 个 \(x_i\) 代入 \(f(x)\) 得到 \(y_i\)，将其表示为二维平面上的点对 \((x_i,y_i)\)。考虑到此时需要解出 \(n\) 个未知系数 \(a_i\)，用 \(n\) 个方程即可。

0.3. 单位复根

0.3.1. 定义

由欧拉公式可知，\(e^{xi}\) 对应的复数的辐角为 \(x\)（弧度制），故 \(e^{2\pi i}\) 对应 \(2\pi\).

假设我们需要把 \(2\pi\) 分成 \(n\) 等份（如下图，\(n=8\)），设一份对应着 \(\omega_n\).

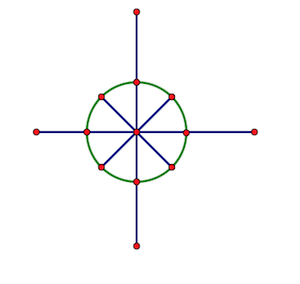
我们需要将 \(\omega_n\) 的辐角加 \(n-1\) 个它本身才是 \(2\pi\).

想到什么了吗？相乘即是模长相乘，幅角相加。

所以有：

\[\omega_n^n=e^{2\pi i} \]

\[\omega_n=e^{\frac{2\pi i}{n}} \]

0.3.2. 性质

\(\omega_n^j=\omega_{n\times k}^{j\times k}\). 这就是 \(e\) 的指数分子分母同时乘上 \(k\)，所以相等。当然，用单位圆理解更加直观。
\(\omega_n^j=-\omega_n^{j+\frac{n}{2}}\). 容易发现就是辐角加上 \(\pi\).
\(\omega_n^n=1\). 显然 \(e^{2\pi i}=1\times (\cos 2\pi +i\sin 2\pi)=1\).

1. 正文

1.1. \(\mathtt{FFT}\) 可以干什么

求两个多项式 \(f,g\) 相乘：\((a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1})\times (b_0+b_1x+b_2x^2+...+b_{m-1}x^{m-1})\). 此时我们需要计算 \(x\) 的 \(0\) 到 \(n+m-2\) 次方项的系数。

虽然我们得到和最终要求的都是系数多项式，可我们发现点值多项式合并只需要 \(y\) 相乘，整体复杂度是 \(\mathcal O(n)\) 的。

如果我们能快速地转换系数多项式与点值多项式，就能快速求解原问题。

朴素是 \(\mathcal O(n^2)\) 的，而 \(\mathtt{FFT}\) 可以优化到 \(\mathcal O(n\log n)\).

1.2. 系数多项式 \(\rightarrow\) 点值多项式

首先，如果想要求出点值多项式，我们得先代入 \(n\) 个 \(x_i\) 以得到 \(n\) 个方程。

傅里叶说：我们选择 \(\omega_n^{i}\ (i\in[0,n))\) 为点值多项式代入的 \(x_i\). 但是显然这样计算 \(n\) 个 \(y_i\) 仍是 \(\mathcal O(n^2)\)，\(\mathtt{FFT}\) 就是用一系列骚操作来快速求 \(y_i\) 的。

\(\mathtt{FFT}\) 的核心实际上是分治。将系数多项式按下标的奇偶分成两个多项式（认为 \(n\) 是 \(2\) 的正整数幂，如果不够可以补 \(0\) 系数）：

\[f_1(x)=a_0+a_2x+a_4x^2+...+a_{n-2}x^{\frac{n}{2}-1} \]

\[f_2(x)=a_1+a_3x+a_5x^2+...+a_{n-1}x^{\frac{n}{2}-1} \]

那么有：

\[f(x)=f_1(x^2)+x\cdot f_2(x^2) \]

那么对于 \(i<\frac{n}{2}\) 就有：

\[f(\omega_n^i)=f_1(\omega_n^{2i})+\omega_n^i\cdot f_2(\omega_n^{2i}) \]

\[=f_1(\omega_{n/2}^{i})+\omega_n^i\cdot f_2(\omega_{n/2}^{i}) \]

\[f(\omega_n^{i+\frac{n}{2}})=f_1(\omega_n^{2i}\cdot \omega_n^n)+\omega_n^{i+\frac{n}{2}}\cdot f_2(\omega_n^{2i}\cdot \omega_n^n) \]

\[=f_1(\omega_{n/2}^{i})-\omega_n^{i}\cdot f_2(\omega_{n/2}^{i}) \]

于是我们先算出 \(f_1,f_2\)，就可以推出 \(f\).

这有什么好处呢？首先可以模拟一下将 \(f\) 拆分成 \(f_1,f_2\) 的过程（下图的 \(x_i\) 即为 \(a_i\)）：

在最底层的单个多项式实际上是一个常数！也就是说我们将求点值多项式的复杂度降低至 \(\mathcal O(n\log n)\)！

如何计算 \(\omega_n\)？用欧拉公式展开得 \(\omega_n=\cos \frac{2\pi}{n}+i\sin\frac{2\pi}{n}\). 注意每层迭代 \(n\) 这个角标都不一样。

1.3. 点值多项式 \(\rightarrow\) 系数多项式

得到的 \(y_i=\sum_{j=0}^{n-1}a_j(\omega_n^i)^j\).

傅里叶说：我们选择 \(\omega_n^{-i}\) 为点值多项式代入的 \(x_i\)，令 \(y_i\) 为新的系数，再做一次。

\[z_i=\sum_{j=0}^{n-1}y_j(\omega_n^{-i})^j \]

\[=\sum_{j=0}^{n-1}a_j\sum_{k=0}^{n-1}(\omega_n^{j-i})^k \]

后面那一坨是等比数列，如果公比不为 \(1\) 时易得为 \(0\)，当公比为 \(1\) 即 \(i=j\) 时为 \(n\).

所以有：

\[z_i=na_i \]

我们就转回去了。

此时的单位复根 \(\omega_n^{-1}=\cos -\frac{2\pi}{n}+i\sin-\frac{2\pi}{n}=\cos \frac{2\pi}{n}-i\sin\frac{2\pi}{n}\).

1.4. 你渴望力量吗？

1.4.1. 蝴蝶变换

上文 \(\mathtt{FFT}\) 的代码实现是递归版的（从上至下），但实际上最底层的单个多项式的排列可以不通过递归来计算，因为它具有一定的规律：

你会发现，新多项式上 \(i\) 号位上存放的 "多项式的下标" \(i\) 的二进制关系是 左右翻转。

知晓这个规律之后，如何快速得到最底层的单个多项式的排列呢？

for(int i=0;i<lim;++i) 
    rev[i] = (rev[i>>1]>>1)|((i&1)<<bit-1);

\(\rm bit\) 是 \(n-1\) 的二进制位数。理解这段代码之前，我们需要知道将一个二进制数左右翻转等价于将其末位放到最高位，将剩余部分翻转接上去，这其实是很经典的 "利用已知信息" 的思想。不过需要注意的是，我们将每个二进制数补全 \(\rm bit\) 位然后翻转，所以 \(i/2\) 的 \(\rm rev\) 值实际上相比我们想要的还有一个后导零，需要再除二。

由此，我们可以从最底层往上推，这样就可以写出 \(\mathtt{FFT}\) 的递推版本了。

1.4.2. 拆系数 \(\mathtt{FFT}\)

\(\text{Link.}\)

1.4.3. 分治 \(\mathtt{FFT}\)

就是求这个东西。

类似 \(\rm cdq\) 分治，先计算出左半边的 \(f\)，再做卷积加入右半边。需要注意的是，我们把 \(g\) 看作一种转移方式，所以每次从 \(0\) 开始截取 \(g\). 时间复杂度两只 \(\log\).

实现时可以预处理 \(\omega_n=g^{\frac{\varphi(p)}{2^n}}\) 来加速。由于 \(\left (g^{\frac{\varphi(p)}{n}}\right )^2=g^{\frac{\varphi(p)}{n/2}}\)，且逆元由相乘等于 \(1\)，其相乘的平方也等于 \(1\)，所以也可以平方递推。

加上自己写的 inc(),dec() 慢了一倍，还不如直接取模。

#include <cstdio>
#define print(x,y) write(x),putchar(y)

template <class T>
inline T read(const T sample) {
	T x=0; char s; bool f=0;
	while((s=getchar())>'9' || s<'0')
		f |= (s=='-');
	while(s>='0' && s<='9')
		x = (x<<1)+(x<<3)+(s^48),
		s = getchar();
	return f?-x:x;
}

template <class T>
inline void write(T x) {
	static int writ[50],tp=0;
	if(x<0) putchar('-'),x=-x;
	do writ[++tp] = x-x/10*10, x/=10; while(x);
	while(tp) putchar(writ[tp--]^48);
}

#include <cstring>
#include <iostream>
using namespace std;

const int maxn = 2e5+5;
const int mod = 998244353;

int n,g[maxn],f[maxn],h[maxn];
int t[maxn],rev[maxn],wn[2][25];

inline int inv(int x,int y=mod-2) {
	int r=1;
	while(y) {
		if(y&1) r=1ll*r*x%mod;
		x=1ll*x*x%mod; y>>=1;
	}
	return r;
}

void preWork() {
	wn[0][23] = inv(wn[1][23]=15311432);
	for(int j=0;j<2;++j)
		for(int i=22;i>=0;--i)
			wn[j][i] = 1ll*wn[j][i+1]*wn[j][i+1]%mod;
}

void NTT(int* f,int lim,bool opt=1) {
	int tmp;
	for(int i=0;i<lim;++i) 
		if(i<rev[i]) swap(f[i],f[rev[i]]);
	for(int mid=1,Log=1;mid<lim;mid<<=1,++Log)
		for(int i=0;i<lim;i+=(mid<<1))
			for(int w=1,j=0;j<mid;++j,w=1ll*w*wn[opt][Log]%mod) {
				tmp = 1ll*w*f[i|j|mid]%mod;
				f[i|j|mid] = (f[i|j]-tmp+mod)%mod;
				f[i|j] = (f[i|j]+tmp)%mod;
			}
}

void dicon(int l,int r,int bit) {
	if(bit<=0 || l>=n) return;
	int mid = l+r>>1;
	dicon(l,mid,bit-1);
	for(int i=0;i<r-l;++i)
		rev[i] = (rev[i>>1]>>1)|((i&1)<<bit-1);
	memcpy(h,f+l,sizeof(int)*(r-l>>1));
	memset(h+(r-l>>1),0,sizeof(int)*(r-l>>1));
	memcpy(t,g,sizeof(int)*(r-l));
	NTT(h,r-l),NTT(t,r-l);
	int Inv = inv(r-l);
	for(int i=0;i<r-l;++i)
		h[i] = 1ll*h[i]*t[i]%mod*Inv%mod;
	NTT(h,r-l,0);
	for(int i=mid;i<r;++i)
		f[i] = (f[i]+h[i-l])%mod;
	dicon(mid,r,bit-1);
}

int main() {
	n=read(9); preWork();
	for(int i=1;i<n;++i)
		g[i]=read(9);
	int bit=0; f[0]=1;
	while((1<<bit)<n) ++bit;
	dicon(0,1<<bit,bit);
	for(int i=0;i<n;++i)
		print(f[i],' ');
	return 0;
}

1.5. 代码实现

#include <cstdio>
#define print(x,y) write(x),putchar(y)

template <class T>
inline T read(const T sample) {
	T x=0; char s; bool f=0;
	while((s=getchar())>'9' || s<'0')
		f |= (s=='-');
	while(s>='0' && s<='9')
		x = (x<<1)+(x<<3)+(s^48),
		s = getchar();
	return f?-x:x;
}

template <class T>
inline void write(T x) {
	static int writ[50],tp=0;
	if(x<0) putchar('-'),x=-x;
	do writ[++tp] = x-x/10*10, x/=10; while(x);
	while(tp) putchar(writ[tp--]^48);
}

#include <cmath>
#include <iostream>
using namespace std;

const int maxn = 4e6+5;
const double PI = acos(-1.0);

struct cp {
	double x,y;
	cp() {}
	cp(const double X,const double Y):x(X),y(Y) {}
	
	cp operator + (const cp& t) {
		return (cp){x+t.x,y+t.y};
	}
	
	cp operator - (const cp& t) {
		return (cp){x-t.x,y-t.y};
	}
	
	cp operator * (const cp& t) {
		return (cp){x*t.x-y*t.y,x*t.y+y*t.x};
	}
} a[maxn],b[maxn],wn,w,tmp;
int n,m,rev[maxn],lim=1,bit;

void preWork() {
	while(lim<n+m-1) lim<<=1,++bit;
	for(int i=0;i<lim;++i)
		rev[i] = (rev[i>>1]>>1)|((i&1)<<bit-1);
}

void FFT(cp *f,int opt) {
	for(int i=0;i<lim;++i)
		if(i<rev[i]) swap(f[i],f[rev[i]]);
	// i<rev[i] 是为避免重复交换
	for(int mid=1;mid<lim;mid<<=1) {
		// mid 是枚举所在递归层 x 对应 f 的长度，其中递归层 x 已经被计算，现在要计算 x 上一层（即从 f_1,f_2 贡献到 f）
		wn = cp(cos(PI/mid),sin(PI/mid)*opt);
		// wn 是 w_{mid*2}，就是 x 上一层的单位复根
		for(int i=0;i<lim;i+=(mid<<1)) {
			w = cp(1,0);
			// w 用来模拟单位复根的几次幂，初始化幅角为 0（cos(0)=1,sin(0)=0）
			for(int j=0;j<mid;++j,w=w*wn) {
				// x 这一层的每一段用 j 来遍历
				tmp = w*f[i+j+mid];
                                // 由于使用的是上一层的单位复根，此时角度只能转到 PI
				f[i+j+mid] = f[i+j]-tmp;
				f[i+j] = f[i+j]+tmp;
			}
		}
	}
}

int main() {
	n=read(9)+1,m=read(9)+1;
	for(int i=0;i<n;++i)
		a[i].x=read(9);
	for(int i=0;i<m;++i)
		b[i].x=read(9);
	preWork(); 
	FFT(a,1),FFT(b,1);
	for(int i=0;i<lim;++i)
		a[i] = a[i]*b[i];
	FFT(a,-1);
	for(int i=0;i<n+m-1;++i)
		printf("%d ",(int)(a[i].x/lim+0.5)); // 虽然结果是正数，但是由于复数运算的数值误差可能会出现接近 0 的负数，所以加一个 0.5
	return 0;
}

posted on 2021-02-02 19:58 Oxide 阅读(430) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部