0. 楔子
"如果要在 \(\text{dag}\) 上表示一个字符串的所有子串该怎么办?"
我们可以把这个字符串的每个后缀都加入一棵字典树(实际上是为了包含每一个可能作为开头的字符),然后从根 \(\rm root\) 开始,在任意节点结束可以走完所有子串,在终止点结束可以走完所有后缀。
但这是 \(n^2\) 级别,遇到稍微大一些的数据,这样的算法就 \(\text{gg}\) 了。
其实你可以发现,如果是插入后缀的话,会有很多重复的节点,如图:
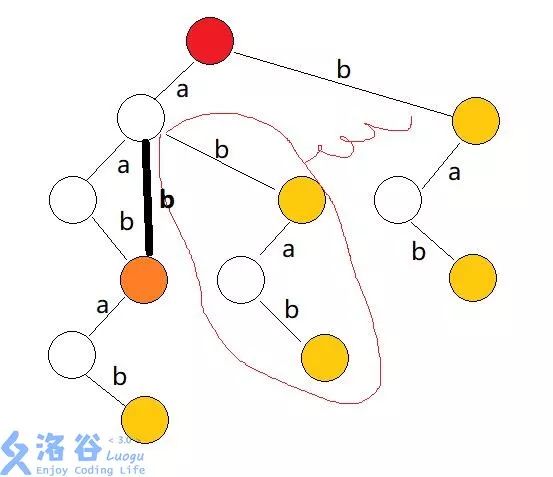
后缀自动机的核心思想就是去除重复节点来优化复杂度。
1. 一些定义及其性质
1.1. \(\text{endpos(s)}\)
- 一个子串在字符串中出现的位置的右端点编号的集合。如,\(\text{S="abcaab",s="ab"}\) 时,\(\text{endpos(s)={2,6}}\).
- 对于 \(\text{endpos}\) 相同的子串形成一个等价类(这是一条定义)。
引理 1:对于任意两子串 \(x,y\ (len_x<len_y)\),则若 \(x\) 是 \(y\) 的后缀,有 \(\text{endpos(y)}\subset \text{endpos(x)}\),反之 \(\text{endpos(x)}\cap \text{endpos(y)}=\emptyset\).
证明:若 \(x\) 是 \(y\) 的后缀,显然有 \(y\) 的地方就有 \(x\),但 \(x\) 出现可能没有 \(y\),显然 \(\text{endpos(y)}\subset \text{endpos(x)}\);反之,有 \(y\) 的地方一定不会出现 \(x\),故有 \(\text{endpos(x)}\cap \text{endpos(y)}=\emptyset\).
引理 2:对于任意等价类将里面的子串按长度从小到大排序。则 \(s_i\) 是 \(s_{i+1}\) 的后缀,且 \(\text{len}_i+1=\text{len}_{i+1}\).
证明:若有 \(x,y,z\) 三个子串,其中 \(x\) 为 \(y\) 的后缀,\(y\) 为 \(z\) 的后缀。据 引理 1 有:
若有 \(\text{endpos(z)}= \text{endpos(x)}\)(即 \(x,z\) 在同一等价类),显然有 \(\text{endpos(x)}=\text{endpos(y)}= \text{endpos(z)}\),则 引理 2 得证。
引理 3:等价类个数级别为 \(n\).
证明:我们设等价类中最长的串为 \(s\),则在 \(s\) 之前添加一个字符的串(设其为 \(s’\))必属于另一个等价类。由 引理 1 可得:\(\text{endpos(s')}\subset \text{endpos(s)}\). 考虑在 \(s\) 之前添加另一个不同的字符(设其为 \(s''\)),由 引理 1 得:\(\text{endpos(s')}\cap \text{endpos(s'')}=\emptyset\). 所以在 \(s\) 前添加字符相当于将 \(\text{endpos(s)}\) 划分成几个集合。考虑初始空串的 \(\text{endpos}\) 设为 \(\{1,2,...,n\}\),我们切割一次相当于划分出两个集合,最多切割 \(n-1\) 次,所以等价类个数应该是 \(2\times (n-1)+1\approx n\) 级别的。
引理 4:设等价类 \(s\) 最长子串长度为 \(\text{len}(s)\),最短子串长度为 \(\text{minlen}(s)\)。定义 \(\text{parent tree}\) 是
引理 3中划分集合(每个等价类就是树上的节点)形成的父子关系,设 \(\text{fa}(s)\) 是 \(s\) 在树上的父亲,则有 \(\text{len}(\text{fa}(s))+1=\text{minlen}(s)\)。
证明:其实比较显然吧。。。
2. 算法
2.1. 一些声明
s[i].to[c]:等价类 \(i\) 最长串末端加字符 \(c\) 的串属于的等价类。定义这种边为实边。s[i].fa:等价类 \(i\) 在 \(\text{parent tree}\) 上的父亲。定义这种边为虚边。- 整串:当前插入的所有字符形成的串。
注意:to[c] 与 fa 边并不是一个玩意。它们只是共用了点(即等价类) 。
2.2. 建树
后缀自动机就是根据一些奇奇怪怪的构造使得:
- 某个等价类 \(x\) 通过实边走向另一个等价类 \(y\) 时,\(x\) 里的串都能通过添加实边边权(即字符)走到 \(y\) 中的某个串。
- 虚边的创建是为了实现上一条原则。显然我们在 \(\text{S="abcbc"}\) 之后添加字符 \(\text b\) 会使 \(\text{abcbc}\) 可以转移到 \(\text{abcbcb}\),使 \(\text{bcbc}\) 转移到 \(\text{bcbcb}\),依此类推(注意,初始位置为 \(4\) 的串 \(\text{bc}\) 能转移到 \(\text{bcb}\) 也即初始位置为 \(2\) 的串 \(\text{bc}\) 能转移)。容易发现,添加字符 \(\text{ch}\) 时,原串的所有后缀都能转移到此后缀 \(\text{+ch}\)。回忆 \(\text{parent tree}\) 上的边是等价类 \(x\) 向 \(x\) 中最长的串前面加上一个字符的串(再提醒一下,这个新串是 \(y\) 中的最小串)所属的等价类 \(y\) 连一条边,而等价类中包含的串都是最长串的后缀,显然 \(x\) 中的串都是 \(y\) 中串的后缀。那么依据虚边的定义,是不是沿着虚边向上跳就能遍历某个串的后缀?是不是就可以实现转移的功能?
知道了我们所需要的,接下来讲讲如何构造。
\(\text{Step 0}\)
int cnt=1; // 后缀自动机的点数
int las=1; // 上一个阶段的整串所属等价类
全赋值为 \(1\) 就是构造 \(\rm root\),这是一个空点,故 s[root].to[c] 代表单个字符 \(\text c\).
\(\text{Step 1}\)
int cur=++cnt;
s[cur].len = s[las].len+1;
创建新的等价类 \(cur\),表示新的整串所属等价类。
\(\text{Step 2}\)
int p=las;
for(; p && s[p].to[c]==0; p=s[p].fa) s[p].to[c]=cur;
寻找上个阶段整串的所有后缀属于的等价类(注意等价类表示了一段连续后缀,显然等价类里后缀的转移是相同的,这也是我们用一个节点代表它们的理由),如果等价类没有边权为 \(\text{ch}\) 的实边,我们就进行转移。
如果等价类已经有边权为 \(\text{ch}\) 的实边了呢?这说明这个等价类 \(+\text{ch}\) 的串已经可以被转移,按照我们的构造,这个等价类的所有后缀属于的等价类 \(\text{+ch}\) 的串显然之前就可以转移了,我们就可以停止这个转移的操作。
\(\text{Step 3}\)
if(!p) s[cur].fa=1;
else {
int q = s[p].to[c];
if(s[q].len==s[p].len+1) s[cur].fa=q;
else {
int now = ++cnt;
s[now]=s[q]; s[now].len=s[p].len+1;
s[q].fa=s[cur].fa=now;
for(; p && s[p].to[c]==q; p=s[p].fa) s[p].to[c]=now;
}
}
las=cur;
接着我们维护虚边。
如果最终 \(p=0\) 就意味着上个阶段整串的后缀没有一个在上个阶段有向 \(\text{ch}\) 的转移(事实上 \(\text{ch}\) 没有出现过)。那么上个阶段整串 \(+\text{ch}\) 的串(即新整串)在 \(\text{parent tree}\) 上就没有父亲,我们将它的虚边直接连向 \(\rm root\).
其它的情况就是我们找到一个等价类 \(p\) 已经有边权为 \(\text{ch}\) 的实边,将这条实边连向的等价类设为 \(q\).
如果有 s[q].len==s[p].len+1,意味着 \(q\) 中的串 完全 可以由 \(p\) 和 \(p\) 的父亲转移而来,因为一条实边只能增加一个字符(注意必须是一次转移)。
你可能会疑惑,难道还有不完全的情况?
就拿 \(\text{S="aaba"}\) 来说吧。
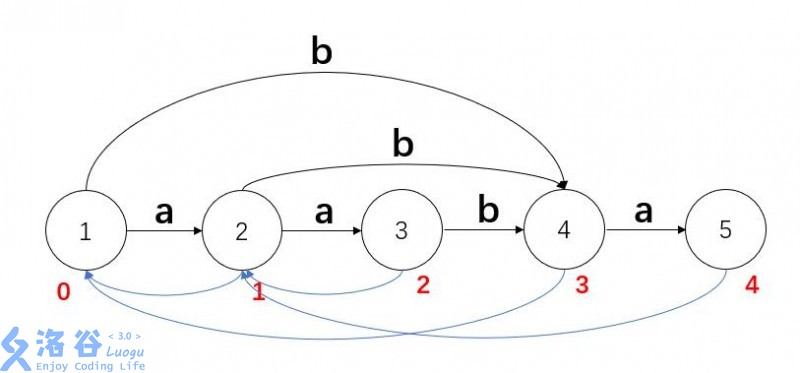
图中有一条 \((2,4)\) 的实边,但能发现节点 \(2\) 只能转移到 \(\text{ab}\) 而不是 \(\text{aab}\)(注意必须是一次转移),而节点 \(4\) 中有 \(\text{aab}\) 是由节点 \(3\) 转移过来的。
回到上文,若 \(q\) 中的串完全可以由 \(p\) 和 \(p\) 的父亲转移而来,显然 \(q\) 中所有的串都是新整串的后缀,只是它们的 \(\text{endpos}\) 不一样:\(q\) 中所有的串不仅之前出现过,现在还会新出现,而新整串到 \(q\) 中最长串 \(+1\) 长度的后缀都是新出现的,所以从 \(cur\) 向 \(q\) 连一条虚边。
如果不完全呢?考虑在 \(\text S\) 后加入字符 \(\text b\) 的情况。
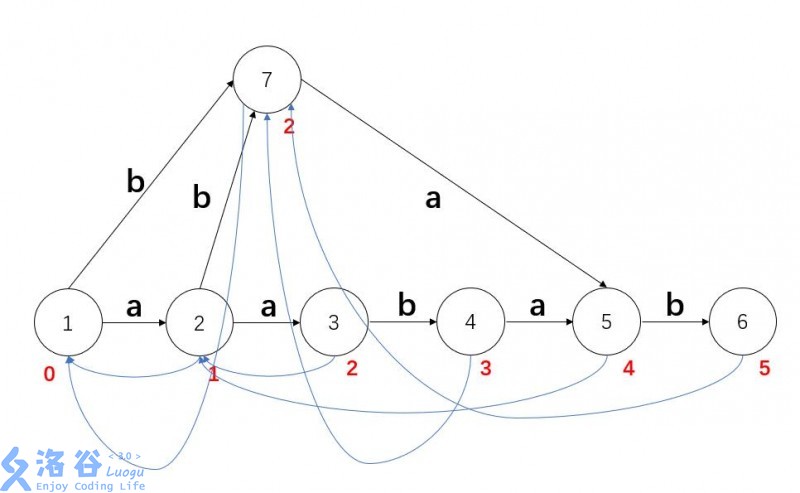
从 \(5\) 跳到 \(2\),发现有权值为 \(\text b\) 的实边通向 \(4\)(即 \(q\))。由于 \(\text{aab}\) 显然不是新整串的后缀,但我们又需要保存这个信息(其实就是 \(\text{endpos}\) 不再相同),怎么办捏?当然是……裂点!新建一个等价类 \(now\) 保存能由 \(p\) 转移的后缀,\(q\) 就只剩下不能被转移的。显然这时 \(cur,q\) 的虚边都连向 \(now\).
完了吗?由于可能之前有等价类将实边连向 \(q\),需要将实边改成连向 \(now\).
3. 时间复杂度
能用就行。啊不是我只是再写下去就要变成写手了。先咕着吧。
4. 应用
先咕着吧。
