0. 前置芝士
0.1. 误差
由于浮点数绝对值越大精度越不精确,需要尽量避免 大数与小数的加减。
尽量少用三角函数,除法,开方,求幂,取对数运算。
对于判断浮点数的大小关系,有以下两种方案:
-
定义
sgn(const double x)计算浮点数的符号:const double eps=1e-9; inline int sgn(const double x) { return x<-eps?-1:x>eps; }利用这个函数就有:
inline int dcmp(const double x,const double y) { return sgn(x-y); } // if x>y, return 1; else return -1 -
乘上 \(10\) 的幂转化成整数。
0.2. 反三角函数
需要注意 定义域!
double x=1.000001;
if(fabs(x-1.0)<eps || fabs(x+1.0)<eps)
x=round(x);
double acx=acos(x);
对于反正切函数,最好使用 cmath::atan2(y,x)。结果为正表示从 \(x\) 轴逆时针旋转的角度,结果为负表示从 \(x\) 轴顺时针旋转的角度。
1. 向量与线
1.1. 转角公式
将向量 \((x,y)=(r\cos \alpha,r\sin \alpha)\) 逆时针旋转 \(\beta\).
1.2. 向量外积
\(|\boldsymbol{a}\times \boldsymbol{b}|\) 等于由向量 \(\boldsymbol{a}\) 和向量 \(\boldsymbol{b}\) 构成的平行四边形的面积。可以理解成矩阵行列式 \(\begin{vmatrix} a.x & b.x \\ a.y & b.y \end{vmatrix}=a.x\cdot b.y-a.y\cdot b.x\). 叉积左右均有分配律。
根据 \(\boldsymbol{a}\times \boldsymbol{b}\) 的正负还可以判断 \(\boldsymbol{a}, \boldsymbol{b}\) 的位置关系(\(\boldsymbol{a}\times \boldsymbol{b}=|\boldsymbol{a}|\cdot |\boldsymbol{b}|\cdot \sin\langle \boldsymbol{a},\boldsymbol{b} \rangle\)):
- \(\boldsymbol{a}\times \boldsymbol{b}=0\):矩阵行列式为 \(0\),那么可以相互线性表示。\(\boldsymbol{a}, \boldsymbol{b}\) 共线。
- \(\boldsymbol{a}\times \boldsymbol{b}>0\):将 \(\boldsymbol{b}\) 转到 \(\boldsymbol{a}\) 的角度顺时针方向较小。
- \(\boldsymbol{a}\times \boldsymbol{b}<0\):将 \(\boldsymbol{b}\) 转到 \(\boldsymbol{a}\) 的角度逆时针方向较小。
1.2.1. 极角排序
点 \(\boldsymbol{o}\) 为极点进行逆时针极角排序。
vec o;
bool cmp(const vec& a,const vec& b) {
double sgn = cross(a-o,b-o);
return (!sgn)?a.x<b.x:sgn>eps;
}
1.3. 点到直线与线段距离
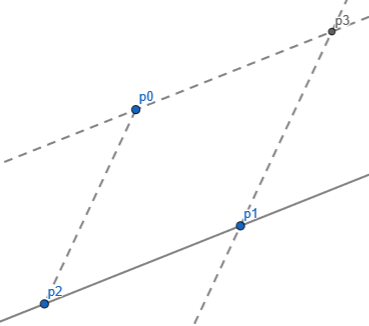
用 \(\boldsymbol{p_2p_0}\) 与 \(\boldsymbol{p_2p_1}\) 外积求出四边形面积,再除以 \(|\boldsymbol{p_2p_1}|\). 线段需要特判一下 \(p_0\) 对 \(p_1p_2\) 的垂足是否落在线段 \(p_1p_2\) 上。
1.4. 判断线段是否相交
首先,通过叉积可以判断点在线段所在直线的哪一侧,例如对于点 \(C\) 与线段 \(AB\),我们可以计算 \(|\boldsymbol{AB}\times \boldsymbol{AC}|\) 来判断。考虑两条线段 \(AB,CD\),若 \((\boldsymbol{AB}\times \boldsymbol{AC})\cdot (\boldsymbol{AB}\times \boldsymbol{AD})>0\) 或者 \((\boldsymbol{CD}\times \boldsymbol{CA})\cdot (\boldsymbol{CD}\times \boldsymbol{CB})>0\),就说明 \(C,D\) 在 \(AB\) 同侧,\(A,B\) 在 \(CD\) 同侧,线段不相交。
相反,如果均为负数,则说明相交。另外一种特殊情况是算出来是零。若只有一个零且另一个为负数,那么显然仍相交;若有两个零,就需要判断其中一条线段的某一个端点是否在另一条线段上。
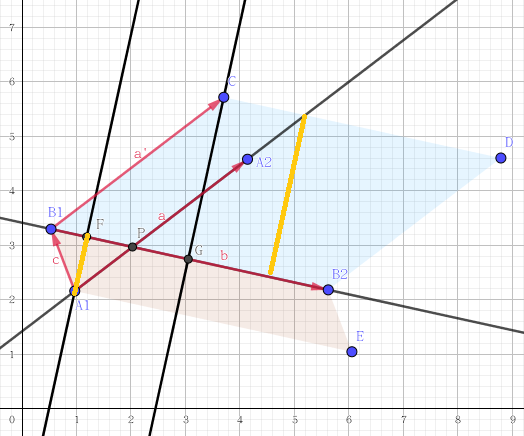
1.5. 求直线交点
先利用跨立实验判断是否相交。接着算出红蓝两块矩形的面积比(有向面积),从而得出两条橙线的比,最后得到向量 \(\boldsymbol{A_1P}\).
2. 多边形
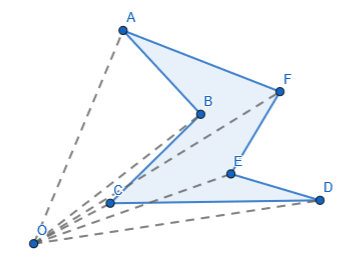
2.1. 多边形面积
任意选点进行三角剖分,即加上多边形相邻点和选点 \(O\) 的叉积。感性理解一下当 \(p_i\) 在 \(p_{i+1}\) 的右手边时加入面积,反之减去面积。
\(\text{Update on 2022.8.7}\):
发现自己之前没有学懂这个算法 🥲,导致一道关于凸包的题调了半天。事实上点的排列顺序是有讲究的,必须按多边形边界排。
这么一说又觉得比较显然了。
2.2. 射线法
用于判断点 \(p\) 是否在多边形内部。从点 \(p\) 引一条射线,若与多边形有奇数个交点则在内部,反之在外部。它还可以处理复杂多边形,就像这样:

不过有引出射线与多边形端点有交点的情况。事实上像这样:
bool inAngle(vec a,vec b,const vec p) {
if(sgn(cross(a,b))<0) swap(a,b);
return sgn(cross(a,p))>=0 and sgn(cross(b,p))<=0;
}
bool InPolygon_1(const vec p,const vector <vec> poy) {
int n=poy.size();
double r=(rand()/double(RAND_MAX)-0.5)*2*pi;
vec v(cos(r),sin(r));
bool ret=0;
for(int i=0;i<n;++i) {
if(onSeg(poy[i],poy[(i+1)%n],p))
return 1;
ret=inAngle(poy[i]-p,poy[(i+1)%n]-p,v)?(!ret):ret;
}
return ret;
}
我们将交点两端的边都计算进去,所以不会有问题。
但是如果射线与多边形的边重合就会出错……不过这种情况很难发生就是了,因为出题人并不知道我是怎么随机射线的……
2.3. 回转数算法
用于判断点 \(d\) 是否在多边形内部。沿多边形走一圈,累计绕点 \(d\) 转了多少角度。
- \(0\)。多边形外。
- \(±\pi\)。多边形上。
- \(±2\pi\)。多边形内。
在实现中并不需要计算转角,只用转象限。最后保证多边形外的点答案为 \(0\) 即可。考虑同样从 \(p_i\) 转到 \(p_{i+1}\),内部和外部的点有什么区别?\(p_i-d\) 与 \(p_{i+1}-d\) 的外积是相反的。利用这个性质就可以规定一个方向来加减象限了。
bool InPolygon_2(const vec p,const vector <vec> poy) {
int n=poy.size(),ret=0;
for(int i=0;i<n;++i) {
if(onSeg(poy[i],poy[(i+1)%n],p))
return 1;
double c=cross(poy[i]-p,poy[(i+1)%n]-p);
double d1=poy[i].y-p.y;
double d2=poy[(i+1)%n].y-p.y;
if(sgn(c)<0 and sgn(d1)<=0 and sgn(d2)>0) ++ret;
if(sgn(c)>0 and sgn(d2)<=0 and sgn(d1)>0) --ret;
}
return ret^0;
}
当然你还可以朴素地直接加象限,就像这样:
int getD(const vec v) {
if(v.x>=0 && v.y>=0) return 0;
if(v.x>=0 && v.y<0) return 3;
if(v.x<0 && v.y<0) return 2;
return 1;
}
bool InPolygon_3(const vec p,const vector <vec> poy) {
int n=poy.size(),ret=0;
for(int i=0;i<n;++i) {
double c=cross(poy[i]-p,poy[(i+1)%n]-p);
if(sgn(c)==0 and sgn(dot(poy[i]-p,poy[(i+1)%n]-p))<=0)
return 1;
int d1=getD(poy[i]-p),d2=getD(poy[(i+1)%n]-p);
if(d2==(d1+1)%4) ++ret;
else if(d2==(d1+3)%4) --ret;
else if(d2==(d1+2)%4) {
if(sgn(c)>=0) ret+=2;
else ret-=2;
}
}
return ret^0;
}
2.4. 动态凸包
#include <cstdio>
#define print(x,y) write(x),putchar(y)
template <class T>
inline T read(const T sample) {
T x=0; char s; bool f=0;
while((s=getchar())>'9' || s<'0')
f |= (s=='-');
while(s>='0' && s<='9')
x = (x<<1)+(x<<3)+(s^48),
s = getchar();
return f?-x:x;
}
template <class T>
inline void write(T x) {
static int writ[50],w_tp=0;
if(x<0) putchar('-'),x=-x;
do writ[++w_tp]=x-x/10*10,x/=10; while(x);
while(putchar(writ[w_tp--]^48),w_tp);
}
#include <map>
using namespace std;
typedef map <int,int> :: iterator type;
# define X first
# define Y second
struct Convex {
map <int,int> c;
long long cross(type& o,type& a,type& b) {
return 1ll*(a->X-o->X)*(b->Y-o->Y)-
1ll*(a->Y-o->Y)*(b->X-o->X);
}
bool in(int x,int y) {
if(c.empty()) return false;
if(c.begin()->X>x || c.rbegin()->X<x) return false;
if(c.count(x)) return y>=c[x];
c[x]=y; type it,pre,nxt;
it = c.lower_bound(x); pre=nxt=it; --pre, ++nxt;
bool In = (cross(it,pre,nxt)>=0);
c.erase(it);
return In;
}
void ins(int x,int y) {
if(in(x,y)) return;
c[x]=y; type it,i,j;
if(c.size()<3) return;
it = c.lower_bound(x);
for(i=it, --i, j=i, --j; it!=c.begin() && i!=c.begin(); i=j--)
if(cross(it,i,j)>=0) c.erase(i); // notice the condition of the loop
else break;
for(i=it, ++i, j=i, ++j; i!=c.end() && j!=c.end(); i=j++)
if(cross(it,i,j)<=0) c.erase(i);
else break;
}
} up,dn;
int main() {
for(int q=read(9); q; --q) {
int opt=read(9), x=read(9), y=read(9);
if(opt==1) up.ins(x,-y), dn.ins(x,y);
else puts((up.in(x,-y) && dn.in(x,y))?"YES":"NO");
}
return 0;
}
2.5. 最小圆覆盖
戳这。
#include <bits/stdc++.h>
using namespace std;
template <class T>
inline T read(const T sample) {
T x=0; char s; bool f=0;
while((s=getchar())>'9' or s<'0')
f|=(s=='-');
while(s>='0' and s<='9')
x=(x<<1)+(x<<3)+(s^48),
s=getchar();
return f?-x:x;
}
const double eps=1e-2,pi=acos(-1.0);
inline int sgn(const double x) {
return x<-eps?-1:x>eps;
}
inline int dcmp(const double x,const double y) {
return sgn(x-y);
} // if x>y, then return 1
struct vec {
double x,y;
vec(const double X=0,const double Y=0):x(X),y(Y){}
vec operator + (const vec t) const {
return vec(x+t.x,y+t.y);
}
vec operator - (const vec t) const {
return vec(x-t.x,y-t.y);
}
vec operator * (const double t) const {
return vec(x*t,y*t);
}
vec operator / (const double t) const {
return vec(x/t,y/t);
}
bool operator < (const vec p) const {
int c=dcmp(x,p.x);
if(c) return c==-1;
return dcmp(y,p.y)==-1;
}
bool operator == (const vec p) const {
return !dcmp(x,p.x) && !dcmp(y,p.y);
}
friend double dot(const vec a,const vec b) {
return a.x*b.x+a.y*b.y;
}
friend double cross(const vec a,const vec b) {
return a.x*b.y-a.y*b.x;
}
double len() const {
return sqrt(dot(*this,*this));
}
vec rot(const double alpha) const {
return vec(x*cos(alpha)-y*sin(alpha),x*sin(alpha)+y*cos(alpha));
}
vec normal() const {
double l=len();
return vec(-y/l,x/l);
}
friend double angle(const vec a,const vec b) {
return acos(dot(a,b)/a.len()/b.len());
}
friend double dis(const vec a,const vec b) {
return sqrt(dot(a-b,a-b));
}
void Read() {scanf("%lf %lf",&x,&y);}
void Print() {printf("%.2f %.2f ",x,y);}
} O;
struct line {
vec p,v;
line(const vec P,const vec V):p(P),v(V){}
friend double dis(const line &l,const vec &p) {
vec v=p-l.p;
return fabs(cross(v,l.v))/(l.v).len();
}
friend bool onLine(const line &l,const vec &p) {
vec v=p-l.p;
return sgn(cross(v, l.v))==0;
}
};
int n;
double r;
vec p[(int)1e5+5],o;
vec GetPoint(const line &l1,const line &l2) {
vec c=l2.p-l1.p;
double t=cross(l2.v,c)/cross(l2.v,l1.v);
return l1.p+l1.v*t;
}
vec Circle(vec &a,vec &b,vec &c) {
return GetPoint(line((a+b)/2,(b-a).normal()),line((a+c)/2,(c-a).normal()));
}
int main() {
while(233) {
n=read(9);
if(!n) break;
for(int i=0;i<n;++i)
p[i].Read();
srand(time(NULL));
random_shuffle(p,p+n);
for(int i=0;i<n;++i)
if(dcmp(dot(p[i]-o,p[i]-o),r)>0) {
o=p[i],r=0;
for(int j=0;j<i;++j)
if(dcmp(dot(p[j]-o,p[j]-o),r)>0) {
o=(p[i]+p[j])/2,r=dot(p[j]-o,p[j]-o);
for(int k=0;k<j;++k)
if(dcmp(dot(p[k]-o,p[k]-o),r)>0)
o=Circle(p[i],p[j],p[k]),
r=dot(p[i]-o,p[i]-o);
}
}
o.Print(),printf("%.2f\n",sqrt(r));
}
return 0;
}
3. 板子
const double eps=1e-9, pi=acos(-1.0);
inline int sgn(const double x) { return x<-eps?-1:x>eps; }
inline int dcmp(const double x,const double y) { return sgn(x-y); }
struct vec {
double x,y;
vec(const double X=0,const double Y=0):x(X),y(Y) {}
vec operator + (const vec& t) const { return vec(x+t.x,y+t.y); }
vec operator - (const vec& t) const { return vec(x-t.x,y-t.y); }
vec operator * (const double& t) const { return vec(x*t,y*t); }
vec operator / (const double& t) const { return vec(x/t,y/t); }
friend double dot(const vec& a,const vec& b) { return a.x*b.x+a.y*b.y; }
friend double cross(const vec& a,const vec& b) { return a.x*b.y-a.y*b.x; }
double len() const { return sqrt(dot(*this,*this)); }
bool operator < (const vec p) const {
int c=dcmp(x,p.x);
if(c) return c==-1;
return dcmp(y,p.y)==-1;
}
bool operator == (const vec p) const {
return !dcmp(x,p.x) && !dcmp(y,p.y);
}
vec rot(const double alpha) const {
return vec(x*cos(alpha)-y*sin(alpha),x*sin(alpha)+y*cos(alpha));
}
vec normal() const {
double l=len();
return vec(-y/l,x/l);
}
friend double angle(const vec a,const vec b) {
return acos(dot(a,b)/a.len()/b.len());
}
void readVec() const { scanf("%lf %lf",&x,&y); }
void printVec() const { printf("(%f,%f)\n",x,y); }
};
struct line {
vec p,v; // l: p+kv
line(const vec& P,const vec& V):p(P),v(V) {}
friend double dis(const line& l,const vec& p) {
return fabs(cross(p-l.p,l.v))/(l.v).len();
}
friend bool onLine(const line& l,const vec& p) {
return sgn(cross(p-l.p,l.v)) == 0;
}
};
double dis(const vec l1,const vec l2,const vec p) {
double d1=dot(p-l1,l2-l1),d2=dot(p-l2,l1-l2);
if(sgn(d1)>=0 && sgn(d2)>=0)
return dis(line(l1,l2-l1),p);
if(sgn(d1)<0) return (p-l1).len();
return (p-l2).len();
}
bool onSeg(const vec& l1,const vec& l2,const vec& p) {
if(!onLine(line(l1,l2-l1),p)) return false;
return sgn(dot(l1-p,l2-p))<=0? true: false;
}
bool SegIntersection(const vec& a1,const vec& a2,const vec& b1,const vec& b2) {
double c1 = cross(a2-a1,b1-a1), c2 = cross(a2-a1,b2-a1);
double c3 = cross(b2-b1,a1-b1), c4 = cross(b2-b1,a2-b1);
int r1 = sgn(c1)*sgn(c2), r2 = sgn(c3)*sgn(c4);
if(r1>0 || r2>0) return false;
if(r1==0 && r2==0) return (onSeg(a1,a2,b1) || onSeg(a1,a2,b2))? true: false;
return true;
}
vec getPoint(const line& l1,const line& l2) {
vec c = l2.p-l1.p; // check whether l1 parallel to l2
if(!sgn(cross(l1.v,l2.v))) return vec(-1e9,-1e9);
double t = cross(l2.v,c)/cross(l2.v,l1.v);
return l1.p+l1.v*t;
}
int getD(const vec v) {
if(v.x>=0 && v.y>=0) return 0;
if(v.x>=0 && v.y<0) return 3;
if(v.x<0 && v.y<0) return 2;
return 1;
}
double getArea(const vector <vec> poy) {
double ans=0;
int n=poy.size();
for(int i=0;i<n;++i)
ans+=cross(poy[i]-O,poy[(i+1)%n]-O);
return fabs(ans)/2;
}
bool inAngle(vec a,vec b,const vec p) {
if(sgn(cross(a,b))<0) swap(a,b);
return sgn(cross(a,p))>=0 and sgn(cross(b,p))<=0;
}
bool InPolygon_1(const vec p,const vector <vec> poy) {
int n=poy.size();
double r=(rand()/double(RAND_MAX)-0.5)*2*pi;
vec v(cos(r),sin(r));
bool ret=0;
for(int i=0;i<n;++i) {
if(onSeg(poy[i],poy[(i+1)%n],p))
return 1;
ret=inAngle(poy[i]-p,poy[(i+1)%n]-p,v)?(!ret):ret;
}
return ret;
}
bool InPolygon_2(const vec p,const vector <vec> poy) {
int n=poy.size(),ret=0;
for(int i=0;i<n;++i) {
if(onSeg(poy[i],poy[(i+1)%n],p))
return 1;
double c=cross(poy[i]-p,poy[(i+1)%n]-p);
double d1=poy[i].y-p.y;
double d2=poy[(i+1)%n].y-p.y;
if(sgn(c)<0 and sgn(d1)<=0 and sgn(d2)>0) ++ret;
if(sgn(c)>0 and sgn(d2)<=0 and sgn(d1)>0) --ret;
}
return ret^0;
}
bool InPolygon_3(const vec p,const vector <vec> poy) {
int n=poy.size(),ret=0;
for(int i=0;i<n;++i) {
double c=cross(poy[i]-p,poy[(i+1)%n]-p);
if(sgn(c)==0 and sgn(dot(poy[i]-p,poy[(i+1)%n]-p))<=0)
return 1;
int d1=getD(poy[i]-p),d2=getD(poy[(i+1)%n]-p);
if(d2==(d1+1)%4) ++ret;
else if(d2==(d1+3)%4) --ret;
else if(d2==(d1+2)%4) {
if(sgn(c)>=0) ret+=2;
else ret-=2;
}
}
return ret^0;
}
vec getCentre(const vector <vec> poy) {
double area=0; int n=poy.size();
vec ret(0,0);
for(int i=0;i<n;++i) {
double t=cross(poy[i]-O,poy[(i+1)%n]-O);
area+=t;
ret.x+=(poy[i].x+poy[(i+1)%n].x)*t;
ret.y+=(poy[i].y+poy[(i+1)%n].y)*t;
}
ret.x/=3,ret.x/=area;
ret.y/=3,ret.y/=area;
return ret;
}
vec cox[1000];
int tp;
void Andrew(const vector <vec> poy) {
int n=poy.size();
vec t[1000];
for(int i=0;i<n;++i) t[i]=poy[i];
sort(t,t+n);
tp=0;
for(int i=0;i<n;++i) {
while(tp>1 and sgn(cross(cox[tp-1]-cox[tp-2],t[i]-cox[tp-1]))<=0)
--tp;
cox[tp++]=t[i];
}
int lim=tp;
for(int i=n-2;i>=0;--i) {
while(tp>lim and sgn(cross(cox[tp-1]-cox[tp-2],t[i]-cox[tp-1]))<=0)
--tp;
cox[tp++]=t[i];
}
if(n>1) --tp;
}
// 计算圆的交的面积
double calc(const vec &o,const double r1,const int i) {
double d=sqrt(dot(o-a[i],o-a[i]));
if(dcmp(d,r1+r[i])>0) return 0;
if(dcmp(d,fabs(r1-r[i]))<0)
return min(r1,r[i])*min(r1,r[i])*pi;
double a1=acos((r1*r1+d*d-r[i]*r[i])/(r1*d*2));
double a2=acos((r[i]*r[i]+d*d-r1*r1)/(r[i]*d*2));
return a1*r1*r1+a2*r[i]*r[i]-sin(a1)*r1*d;
}
int main() {
return 0;
}
/*
point line_intersection(point a,point a0,point b,point b0)
{
double a1,b1,c1,a2,b2,c2;
a1 = a.y - a0.y;
b1 = a0.x - a.x;
c1 = cross(a,a0);
a2 = b.y - b0.y;
b2 = b0.x - b.x;
c2 = cross(b,b0);
double d = a1 * b2 - a2 * b1;
return point((b1 * c2 - b2 * c1) / d,(c1 * a2 - c2 * a1) / d);
}
*/
4. 一些题
例 1. \(\text{Segments}\):给定 \(n\le 100\) 条线段,判断是否存在一条直线使得所有线段在直线上的投影有交点。
问题可以转化为是否存在一条直线经过所有线段,这条直线与我们要求的直线垂直。一定存在这样的直线经过线段的端点,所以可以直接枚举。
例 2. \(\text{That Nice Euler Circuit}\)
题目有一些比较重要的性质:
- \(p_i\neq p_{i-1}\)。
- 欧拉机器绝对不会画出任何与其他已经画出的线重叠的线。然而,这两条线也可能相交。
欧拉定理:设 \(G\) 为任意的连通的平面图,则 \(v-e+f=2\),\(v\) 是 \(G\) 的顶点数,\(e\) 是 \(G\) 的边数,\(f\) 是 \(G\) 的面数。
首先枚举给出线段求出所有交点,不过交点会有重合,用 std::unique() 即可。枚举所有交点 \(i\),给出线段 \(j\),如果 \(i\) 在 \(j\) 上(不包含端点)就增加一条边。
为什么?题目保证没有重叠的线,所以交点不会划分已划分的线段。
例 3. \(\text{CodeForces - 1C Ancient Berland Circus}\)
首先多边形一定在三角形的外接圆上,否则三个端点不可能和多边形端点重合。其次应使多边形端点尽量少,从而最小化面积。
利用正弦定理可知 \(r=\frac{abc}{4S}\)。三角形每条边对应的圆心角度数是 \(\arccos (\frac{2r^2-l^2}{2r^2})\)。
将圆心角度数取 \(\gcd\) 可以最大化中心角,从而最小化多边形顶点数。第三个圆心角可以直接取 \(2\pi-\alpha-\beta\) 因为它要么是 \(\alpha+\beta\) 要么是 \(2\pi-\alpha-\beta\),
例 4. \(\text{UVA - 10256 The Great Divide}\)
判断两个凸包是否相交。
- 是否有相交线段。特判凸包退化成线段的情况。
- 点是否在另一凸包内。这是为了判断凸包相互包含的情况。
例 5. \(\text{[CQOI 2017] }\)小Q的草稿
首先盲猜一个 \(\mathcal O(n^2\log n)\) 的复杂度,然后就有一个思路:枚举点 \(x\),考虑能和它连接的点。由于三角形中不包含点,所以三角形中实际上只有一条边有用,就是占据点 \(x\) 极角范围最大的边。然后将边和点都按照极角排序,扫描线地进行 \(\rm check\).
如何 \(\rm check\)?枚举点 \(x\) 后,按极角排序枚举点 \(y\),找到在点 \(y\) 方向上离点 \(x\) 最近的线段("\(y\) 方向上的距离" 就是连接 \(x,y\) 与线段形成的交点和 \(x\) 的距离),再判断 \(y\) 与 \(x\) 的距离是否小于线段与 \(x\) 在 \(y\) 方向的距离即可。问题是怎么快速查找线段?我们首先将插入线段转化成按极角序插入两个点(入点为加入线段,出点为删除线段),用一个 \(\rm set\) 维护线段,每次遍历到入点时,将 \(\rm set\) 的比较器改成入点(这个 \(\rm set\) 为以在比较器方向上的距离更小作为优先),然后再插入线段。查询直接用 \(\rm set\) 的 begin() 即可。
这为啥是对的呢?事实上,\(\rm set\) 内部维护了一棵平衡树,当改变比较器时,树的结构并不会发生变化,只有当新插入元素时才会 按新的优先级插入元素。由于三角形不会有交,也就是线段没有交,这个方法才是正确的。
另外再讲一个细节:由于我们用 atan2() 函数求极角,点实际是按照 "三四一二" 象限的顺序来排列的。在最开始要先插入区间为二四象限的线段。
例 6. 给出 \(n\) 个点,求一共能形成多少个凸四边形(保证两点不重合,三点不共线)。\(n\leqslant 1000\).
逆向思维。凹四边形一定形态类似于一个三角形包含一个点,于是可以枚举被包含点 \(o\),数包含它的三角形个数。枚举三角形中某点 \(p\),连接 \(op\)(连接什么啊?),粗略地发现另外两点一定在 \(op\) 两侧,然而这必要却不充分。
由于三角形包含与不包含点 \(o\) 是对立事件,所以另外两点在 \(op\) 同侧(这是异侧的对立事件)可以 充分地 推出三角形不包含点 \(o\)。于是我们再用一次逆向思维 —— 数有多少个三角形不包含点 \(o\).
事实上,将 \(o\) 点以外的点极角排序,只需数 \(op\) 逆时针转一百八十度之内的点即可(顺时针不用数)。
注意极角排序。需要设定一个初始象限,不然会乱排。复杂度 \(\mathcal O(n^2\log n)\).
