\(\text{Bi Bi Time!}\)
那是一天之前,亲爱的教练为我们拉了一套 提高组 难度题目,无人上 \(100 \text{pts}\)。
\(\text{Solution}\)
\(\mathtt{dp}\) 做法
首先有个结论:被钦定节点的所有子树大小不超过 \(\lfloor \frac{n}{2}\rfloor\)。
这个结论来源一个寻找最优解的思路:假设 \(v,u\) 之间有一条边,我们可以把以 \(u\) 为根节点的树除去 \(v\) 这棵子树的一团子树称为左子树(\(x\)),把以 \(v\) 为根节点的树除去 \(u\) 这棵子树的一团子树称为右子树(\(y\))。
那么假设我们求出 \(u\) 的距离和是 \(dis\),\(v\) 的距离和就是 \(dis+(size_x+1)-(size_y+1)=dis+size_x-size_y\)。那么如果现在有 \(size_x<size_y\),\(v\) 是会比 \(u\) 更优的,一直这样走下去,发现当 \(size_x=size_y\) 时再走就会更劣。此时的 \(u,v\) 就是最优解(当然这是偶数的情况,奇数就只有一个是最优解)。
所以结论得证。
那问题就转化成切多少刀可以使此点的每个子树大小不超过 \(\lfloor \frac{n}{2}\rfloor\)。好吧到这一步我还是不会做。
贪心地想,我们砍边的花费都是一样的,每次肯定尽量砍 \(size\) 最大的子树(至于子树的大小限制我们就直接怼给子树自己来做就行了)。
定义 \(f[u]\) 为使 以 \(u\) 为根的子树的大小不超过 \(\lfloor \frac{n}{2}\rfloor\) 的最小砍次数,\(tot[u]\) 为砍完之后还剩多少个点。
注意这里子树 \(f[u_{son}]\) 的最优解一定会贡献给 \(f[u]\),因为就算把整棵子树 \(u_{son}\) 砍下来,如果不能维持其大小不超过 \(\lfloor \frac{n}{2}\rfloor\) 也是白搞。
我们先只管子树的情况做一遍 \(\text{dfs}\),关于上面父亲那一坨的情况就是换根 \(\mathtt{dp}\)。
第一遍 \(\text{dfs}\) 能得到根节点的答案,后面的 \(\mathtt{dp}\) 就是需要维护父亲那一坨大小不超过 \(\lfloor \frac{n}{2}\rfloor\),把父亲的 \(tot[fa_{son}]\) 和父亲的父亲那一坨剩下的 \(tot\) 排个序,依次选取即可,不过因为对于父亲的每个儿子都要排除自己的 \(tot\),所以像第一遍 \(\text{dfs}\) 的直接线性选取不行,做个前缀和二分即可。
总时间复杂度 \(\mathcal O(n \log n)\)。
瞪眼法
经 \(\color{#F00}{\rm E}\color{#000}{\rm mm\_titan}\) 的提醒,我看到了一个快又短的解法!
我们先找出整棵树的重心 \(o\),那么当我们钦定 \(x\) 为根时,\(o\) 在超重的子树中,因为 \(o\) 保证了每个子树大小 \(\le \left \lfloor \frac{n}{2}\right \rfloor\)。
有了这个观察,我们惊喜地发现并不需要对于每个节点都求出 \(f[i]\),事实上,我们只需要求出 \(f[o]\)。我们给 \(o\) 的子树的 \(siz\) 从大到小排序,假设选取到第 \(p\) 个子树满足了条件,且前 \(p\) 个子树 \(siz\) 和为 \(sum\)。
为了帮助理解,画了一张图:
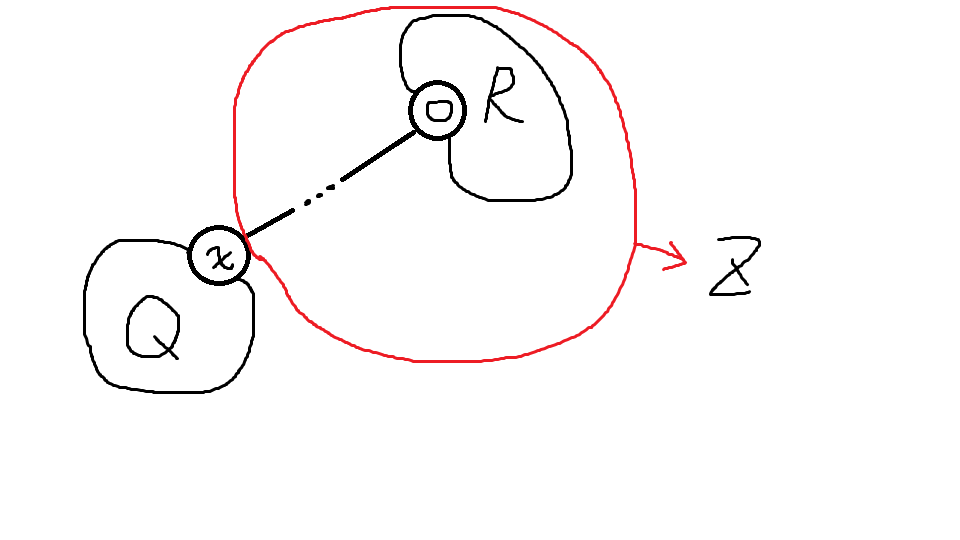 其中 \(x\) 在 \(o\) 的某棵子树 \(i\) 中,\(Q\) 是在以 \(o\) 为根时 \(x\) 的子树。\(R\) 是 \(o\) 除了 \(i\) 之外的子树,\(Z\) 是 \(\{x\}\cup Q\) 的补集。
其中 \(x\) 在 \(o\) 的某棵子树 \(i\) 中,\(Q\) 是在以 \(o\) 为根时 \(x\) 的子树。\(R\) 是 \(o\) 除了 \(i\) 之外的子树,\(Z\) 是 \(\{x\}\cup Q\) 的补集。
对每棵子树 \(i\) 单独进行 \(\rm dfs\)。如果 \(i\le p\),我们先不砍这个子树,因为以 \(i\) 为根时 \(o\) 只用砍剩余 \(p-1\) 个就满足条件了,不过需要判断 \(i\) 到 \(o\) 的路径上是否有需要割的子树;如果 \(i>p\),由于砍前 \(p\) 个子树是最优方案,但我们砍另外 \(p\) 个子树也有可能合法:于是我们先不砍 \(p\) 子树,这带给我们的损失最小,然后判断是否需要割子树。
关于割子树的判断,我们可以计算 \(x\) 的子树(以 \(o\) 为根时,包括自己)和已经被割子树大小之和 \(num=siz[x]+sum-\max\{siz[i],siz[p]\}\)。
容易发现,剩余的点都在以 \(x\) 为根时,\(o\) 所存在的那个子树内。那么若 \(2\times num< n\),就说明 \(o\) 所在的那个子树超重,还是需要割 \(p\) 刀。
总时间复杂度 \(\mathcal O(n \log n)\),当然你可以优化排序做到 \(\mathcal O(n)\)。
\(\text{Code}\)
\(\mathtt{dp}\) 做法
#include <cstdio>
#define rep(i,_l,_r) for(register signed i=(_l),_end=(_r);i<=_end;++i)
#define fep(i,_l,_r) for(register signed i=(_l),_end=(_r);i>=_end;--i)
#define erep(i,u) for(signed i=head[u],v=to[i];i;i=nxt[i],v=to[i])
#define efep(i,u) for(signed i=Head[u],v=to[i];i;i=nxt[i],v=to[i])
#define print(x,y) write(x),putchar(y)
template <class T> inline T read(const T sample) {
T x=0; int f=1; char s;
while((s=getchar())>'9'||s<'0') if(s=='-') f=-1;
while(s>='0'&&s<='9') x=(x<<1)+(x<<3)+(s^48),s=getchar();
return x*f;
}
template <class T> inline void write(const T x) {
if(x<0) return (void) (putchar('-'),write(-x));
if(x>9) write(x/10);
putchar(x%10^48);
}
template <class T> inline T Max(const T x,const T y) {if(x>y) return x; return y;}
template <class T> inline T Min(const T x,const T y) {if(x<y) return x; return y;}
template <class T> inline T fab(const T x) {return x>0?x:-x;}
template <class T> inline T gcd(const T x,const T y) {return y?gcd(y,x%y):x;}
template <class T> inline T lcm(const T x,const T y) {return x/gcd(x,y)*y;}
template <class T> inline T Swap(T &x,T &y) {x^=y^=x^=y;}
#include <algorithm>
using namespace std;
const int maxn=1e6+5;
int n,head[maxn],nxt[maxn<<1],to[maxn<<1],cnt,f[maxn],tot[maxn],lim,ans[maxn],pre[maxn],fa_f[maxn],fa_tot[maxn];
struct node {
int x,y;
} p[maxn];
void addEdge(int u,int v) {
nxt[++cnt]=head[u],to[cnt]=v,head[u]=cnt;
nxt[++cnt]=head[v],to[cnt]=u,head[v]=cnt;
}
bool cmp(node a,node b) {
return a.x<b.x;
}
void dfs1(int u,int fa) {
tot[u]=1;
erep(i,u) {
if(v==fa) continue;
dfs1(v,u);
f[u]+=f[v],tot[u]+=tot[v];
}
if(tot[u]<=lim) return;
int Cnt=0;
erep(i,u) if(v^fa) p[++Cnt].x=tot[v];
sort(p+1,p+Cnt+1,cmp);
while(tot[u]>lim) tot[u]-=p[Cnt--].x,++f[u];
}
void dfs2(int u,int fa) {
ans[u]=fa_f[u]; int Cnt=0,l,r,mid,ToT,F,res;
erep(i,u) if(v^fa) ans[u]+=f[v],p[++Cnt]=(node){tot[v],v};
p[++Cnt]=(node){fa_tot[u],fa};
sort(p+1,p+Cnt+1,cmp);
rep(i,1,Cnt) pre[i]=pre[i-1]+p[i].x;
rep(i,1,Cnt) {
if(p[i].y==fa) continue;
l=1,r=Cnt;
while(l<=r) {
mid=l+r>>1;
ToT=pre[mid]+1,F=mid; // 枚举 mid 个可以剩下,其中 +1 是 u(因为对于 u 的儿子,把 (u,v) 砍了显然没有任何意义)
if(i<=mid) ToT-=p[i].x,--F;
if(ToT<=lim) res=mid,l=mid+1;
else r=mid-1;
}
ToT=pre[res]+1,F=res;
if(i<=res) ToT-=p[i].x,--F;
fa_tot[p[i].y]=ToT,fa_f[p[i].y]=ans[u]-f[p[i].y]+Cnt-F-1;
}
erep(i,u) if(v^fa) dfs2(v,u);
}
int main() {
int u,v;
n=read(9); lim=n>>1;
rep(i,1,n-1) {
u=read(9),v=read(9);
addEdge(u,v);
}
dfs1(1,0); dfs2(1,0);
rep(i,1,n) print(ans[i],'\n');
return 0;
}
瞪眼法
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
#define print(x,y) write(x),putchar(y)
template <class T> inline T read(const T sample) {
T x=0; int f=1; char s;
while((s=getchar())>'9'||s<'0') if(s=='-') f=-1;
while(s>='0'&&s<='9') x=(x<<1)+(x<<3)+(s^48),s=getchar();
return x*f;
}
template <class T> inline void write(const T x) {
if(x<0) return (void) (putchar('-'),write(-x));
if(x>9) write(x/10);
putchar(x%10^48);
}
const int maxn=1e6+6;
int n,cnt,p[maxn],rt;
int siz[maxn],ms[maxn];
int head[maxn],ans[maxn];
int pos,num;
struct Edge {
int to,nxt;
} e[maxn<<1];
void addEdge(int u,int v) {
e[++cnt].to=v,e[cnt].nxt=head[u],head[u]=cnt;
e[++cnt].to=u,e[cnt].nxt=head[v],head[v]=cnt;
}
void dfs(int u,int fa) {
siz[u]=1;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].to;
if(v==fa) continue;
dfs(v,u);
siz[u]+=siz[v];
ms[u]=max(ms[u],siz[v]);
}
ms[u]=max(ms[u],n-siz[u]);
if(ms[u]<ms[rt]) rt=u;
}
bool cmp(int a,int b) {
return siz[a]>siz[b];
}
void Work(int u,int fa,int val) {
ans[u]=pos;
if(2*(siz[u]+val)>=n) --ans[u];
for(int i=head[u];i;i=e[i].nxt)
if(e[i].to^fa)
Work(e[i].to,u,val);
}
int main() {
n=read(9);
int u,v; ms[0]=1e9;
for(int i=1;i<n;++i) {
u=read(9),v=read(9);
addEdge(u,v);
}
dfs(1,0),dfs(rt,0);
for(int i=head[rt];i;i=e[i].nxt)
p[++num]=e[i].to;
sort(p+1,p+num+1,cmp);
int sum=0;
for(int i=1;i<=num;++i)
if((sum+siz[p[i]])*2>=n) {
sum+=siz[p[i]];
pos=i; break;
}
else sum+=siz[p[i]];
for(int i=1;i<=num;++i)
Work(p[i],rt,sum-max(siz[p[i]],siz[p[pos]]));
for(int i=1;i<=n;++i)
print(ans[i],'\n');
return 0;
}
