Codeforces Round #801 (Div. 2) and EPIC Institute of Technology Round

C. Zero Path

只用 \(\mathtt{dp}\) 出 \(\text{mx}(i,j),\text{mn}(i,j)\) 分别表示从 \((1,1)\) 到 \((i,j)\) 能得到的最大权值，判断 \(0\) 是否在 \([\text{mn}(n,m),\text{mx}(n,m)]\) 之间即可。

考虑合法的图一定满足 \(2\mid (n+m-1)\)，所以到 \((n,m)\) 的路径和一定满足是偶数。考虑 \(\text{mx}(n,m)\) 路径上一个 \((i,j),(i,j-1),(i+1,j)\) 的一个折角，可以转化成 \((i+1,j-1),(i,j-1),(i+1,j)\) 的折角（其它情况类似），权值变化只能为 \(-2/0/2\)，所以当 \(0\) 在 \([\text{mn}(n,m),\text{mx}(n,m)]\) 之间时，一定能在调整过程中经过 \(0\).

D. Tree Queries

这题在 \(\text{AtCoder}\) 上有原题：\(\text{APC001E - Antennas on Tree}\).

首先一个 observation 是当一个点连接 \(s\) 个连通块时，必须选 \(s-1\) 个连通块中放置关键点。我们考虑如何将这个观察应用到树上，可以先选一个度数至少为 \(3\) 的点（显然如果不存在这样的点答案即为 \(1\)）为根，这样每个点的父亲方向连通块一定包含一个关键点，所以就只需要考虑子树的情况了。复杂度 \(\mathcal O(n)\).

E. Ambiguous Dominoes

一些闲话：能把骨牌的构造转到树上 \(\rm dfs\) 序的人都是神仙吧！我拿到这种题真的一点思路都没有啊！悲剧啊 😭！但说实话，我更倾向于出题人是逆向出的这道题。

首先考虑将骨牌转化成图论问题 —— 将骨牌上的数字转成点，将连接两点的骨牌转成边。接着从连通块的点 \(u\) 开始进行这样的遍历：

void dfs(int i) {
    lst.push_back(i);
    if(!used[i]) {
        used[i] = true;
        for(pair <int,int> p: graph[i])
            if(!usedEdges[p.second]) {
                usedEdges[p.second] = true;
                dfs(p.first);
                lst.push_back(i);
            }
    }
}

不妨设此连通块中 边的条数 为 \(k\)，可以发现，最后 \(\rm lst\) 中存储的序列长度为 \(2k+1\)，这由每条边都会被塞进去的两个端点，再加上最开始遍历 \(u\) 进行的加入组成。

另外，对于 \(\forall i\in[1,2k]\)，都有 \(\text{lst}_i,\text{lst}_{i+1}\) 对应一条边。显然，对于每条边 \((u,v)\)，都有 \(u\rightarrow v\) 和 \(v\rightarrow u\) 出现在序列中。

可以证明，对于每条边 \((u,v)\)，其 \(u\rightarrow v\) 和 \(v\rightarrow u\) 出现在序列中的位置（不妨定义 "位置" 为第一个点的位置）的奇偶性是不同的。先考虑 "无用边" 也就是另一个端点已经被遍历过的边，其 \(u\rightarrow v\) 和 \(v\rightarrow u\) 出现在序列中的位置是连续的，奇偶性肯定不同。接着我们可以删掉那些边，每删掉一条边相当于在序列中删掉两个连续的点，这样是不影响其它边出现位置的奇偶性的。至此，剩下的边就是对连通块的一个 \(\rm dfs\) 序遍历，那么一条边的遍历与回溯之间边的遍历与回溯次数一定为偶数，所以它们奇偶性不同。

这个结论可以帮助我们构造 \(2\times n\) 的多米诺骨牌矩阵。由于序列的第一条边和最后一条边一定是关于 \(u\) 的边，所以骨牌矩阵可以看作一个环（就是下图用橙色标记的部分）：

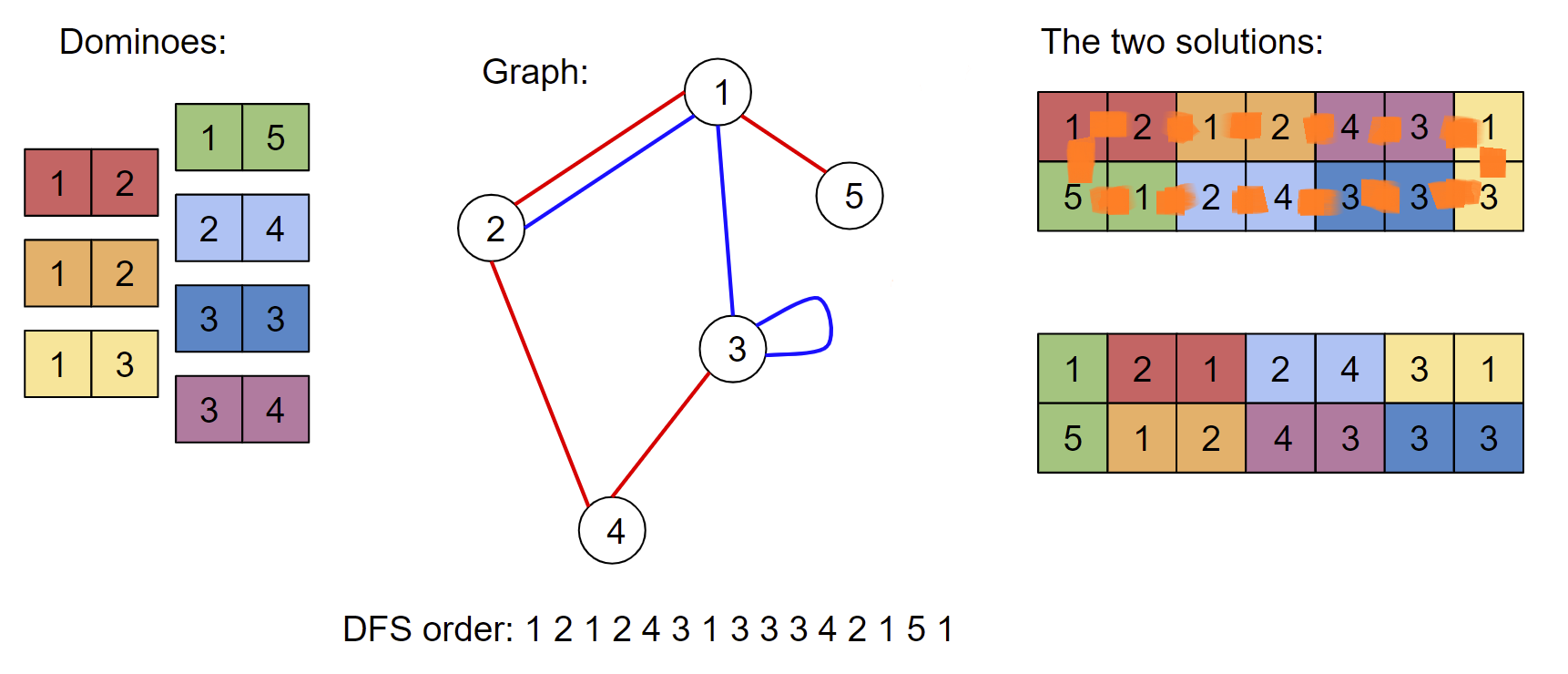
于是可以先选奇数位的边，再选偶数位的边。由于同一条边的遍历与回溯奇偶性不同，所以每条边会且只会被选择一次。